Сила і системи сил

Досвід людства показує, що стан рівноваги чи руху матеріального тіла залежить від його взаємодії із зовнішнім середовищем. В теоретичній механіці розглядається тільки механічна взаємодія, яка спричиняє зміну характеру руху матеріальних тіл, або їх деформацію.

Величина, яка є мірою механічної дії (тиск, притягання, відштовхування) одного матеріального тіла на друге, називається силою.

Поняття сили в механіці – основне, первинне поняття. За своєю природою сила – величина векторна і тому як усякий вектор визначається модулем (величиною), точкою прикладання і напрямом у просторі. Пряма, уздовж якої напрямлений цей вектор, називається лінією дії сили (рис.1).

Лінія дії сили

Рис.1

Надалі позначатимемо сили літерами латинського алфавіту зі знаком вектора:, а їх величини (модулі) тими ж літерами без позначки вектора, або з використанням знаку модуля: чи

За одиницю сили в системі СІ прийнято 1 Ньютон; . Часто використовують кратні одиниці сили: і .

Системою сил називають сукупність сил, які діють на даний матеріальний об’єкт. Системи сил можуть бути просторовими (окремі сили системи довільно розташовані у просторі) і плоскими (всі сили системи діють в одній певній площині).

Просторові чи плоскі системи сил, лінії дії яких перетинаються в одній точці (точка сходу), називають збіжними.

Систему, що складається з сил, позначають так: або скорочено .

Дві системи сил називають еквівалентними, якщо при заміні однієї системи сил, що діє на матеріальний об’єкт, іншою системою стан спокою або характер руху даного об’єкта не порушується. Еквівалентність систем сил позначають таким чином: або

Зрівноваженою (еквівалентною нулю) системою сил називають таку систему, під дією якої матеріальний об’єкт не змінює свого стану спокою чи руху за інерцією. Позначення: .

У випадках, коли система сил еквівалентна одній силі, то ця сила називається рівнодіючою даної системи сил. Математично це записується так:

Проекція сили на вісь

Проекцією вектора сили на будь-яку координатну вісь називають напрямлений відрізок, величина якого дорівнює добутку модуля вектора сили на косинус кута, утвореного напрямом вектора сили з додатним напрямом осі.

Так, наприклад, проекція сили на вісь (рис.2) визначається з рівняння:

.

(1)

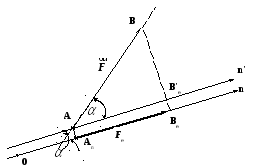
Рис.2.

Як можна бачити з цього ж рисунка, проекції вектора на паралельні і однаково напрямлені осі рівні між собою, тобто: .

Тому часто зручніше проектувати вектор на вісь, паралельну даній, яка проходить через початок вектора.

З рівняння (1) виходить, що у випадках, коли кут між вектором сили і додатним напрямом осі гострий, проекція сили додатна, якщо тупий – від’ємна, а коли сила перпендикулярна до осі, то її проекція дорівнює нулю.

Розв’язання задач теоретичної механіки з використанням прямокутної системи координатних осей досить часто вимагає визначення проекцій векторів (сил, швидкостей) на обрані осі. Тому доцільно звернути увагу на зв’язок між собою величин проекцій.

П

у

рипустимо, що сила розташована в площині (рис.3) і утворює з віссю тупий кут , або гострий кут ().

Згідно з визначенням проекції сили будемо мати:

або ;

;

Рис. 3 або .

Таким чином, якщо при визначенні величини проекції сили на одну з осей при модулі сили множником є косинус кута, то величина проекції на іншу вісь дорівнюватиме добутку модуля сили на синус того ж кута.

При визначенні проекції довільної системи сил на певну координатну вісь користуються теоремою векторної алгебри: проекція векторної суми на координатну вісь дорівнює алгебраїчній сумі проекцій складових на цю вісь. Так, наприклад, проекція системи сил на вісь х :

.

(2)

В частинному випадку, коли система сил має рівнодіючу , її проекції на осі декартової системи координат будуть виражатися рівняннями:

; ; .

(3)

Силу, як і будь-який інший вектор, можна виразити через її проекції на осі координатної системи :

,

де - одиничні вектори (орти) осей x,y і z відповідно.

Тоді модуль сили буде дорівнювати:

.

(4)

Косинуси кутів, які утворює вектор сили з координатними осями, визначаються співвідношеннями:

.

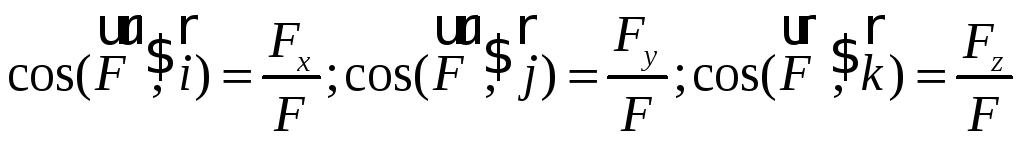(5)

Приклад 1. До твердого тіла в точці А прикладена система збіжних сил , розташованих в площині хAy. Визначити величину і напрям рівнодіючої цієї системи, якщо кут .

Розв’язок: рівнодіюча системи збіжних сил , а її проекції на координатні осі Ах і Ау відповідно будуть дорівнювати:

;

.

Визначаємо величини проекцій заданої системи сил на обрані осі:

; ; ;

; ; .

Відповідно проекції рівнодіючої:

;

.

З отриманих результатів виходить, що величина рівнодіючої Н; вектор рівнодіючої напрямлений по осі Ах.

Приклад 2. Відомі проекції на осі координат і рівнодіючої плоскої системи збіжних сил і , а також проекції цих сил на ті ж осі: , , , . Визначити модуль сили .

Розв’язок. Так як , а , то проекції шуканої сили будуть:

,

.

Тоді модуль сили :

.