§ 6.10. Дисперсія світла

Дисперсією світла називається залежність абсолютного показника заломлення речовини n від частоти світла  або від довжини хвилі , тобто

Рис.6.27

. (6.50)

Це явище спостерігається під час взаємодії світла з речовиною. Результатом дисперсії є розкладання в спектр білого світла, яке проходить через прозору скляну призму.

Якщо , то дисперсія світла в середовищі називається нормальною, тобто зі збільшенням частоти хвилі показник заломлення зростає. У випадку, коли , дисперсія світла називається аномальною (рис. 6.27).

Нормальна дисперсія світла спостерігається поза смугами або лініями поглинання, аномальна – в межах смуг або ліній поглинання. Так, для скла смуги поглинання розміщені в ультрафіолетовій та інфрачервоній частинах спектру.

Класична електронна теорія пояснює дисперсію як результат взаємодії електромагнітних хвиль з електронами речовини. Нехай на прозорий діелектрик падає світлова хвиля. Тоді на його зв’язані електрони (e) з боку електричної компоненти електромагнітного поля діє сила

, (6.51)

де E₀ – амплітудне значення електричної компоненти електромагнітної хвилі. Внаслідок взаємодії електронів з атомами виникає квазіпружна повертаючи сила

,

де m – маса електрона, ₀ – його власна частота коливань, x – зміщення електрона.

Електрони діелектрика здійснюють вимушені коливання, що описуються диференціальним рівнянням

.

Звідси знаходиться зміщення електрона під дією електричного поля світлової хвилі

(6.52)

З курсу «Електрики» відомо, що діелектрична проникливість середовища під час поляризації діелектрика визначається за формулою

де  – діелектрична сприйнятливість середовища; P_e – проекція вектора поляризації на напрям вектора напруженості електричного поля. З іншого боку, показник заломлення для прозорих середовищ ()

.

Отже,

.

Для діелектриків, атоми яких мають лише один “оптичний” електрон, проекція вектора поляризації (поляризованість)

,

де n₀ – концентрація атомів; p_e – наведений дипольний електричний момент атома.

Знак мінус показує, що вектор P_e напрямлений протилежно до зміщення x. Тоді показник заломлення діелектрика

. (6.53)

Враховуючи (6.52), дістанемо

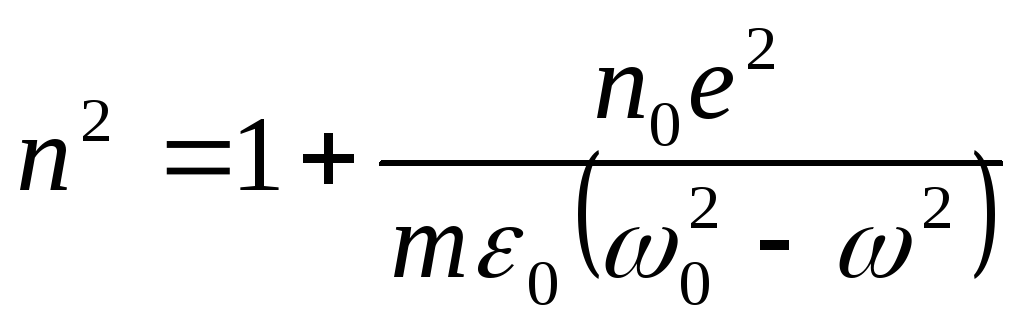. (6.54)

Необмежене зростання n при фізичного змісту не має і практично нездійсненне. Такий результат дістали тому, що не взяли до уваги втрати енергії на випромінювання вторинних електромагнітних хвиль, співудари між атомами, що випромінюють. Наближено ці втрати можна врахувати, коли припустити, що на кожний електрон діє сила опору, пропорційна до його швидкості:

де r – коефіцієнт опору. Тепер диференціальне рівняння вимушених коливань оптичного електрона набуває вигляду:

.

Розв’язок цього рівняння веде до такого виразу для показника заломлення:

. (6.55)

Ця залежність описує криву дисперсії, зображену на рис. 6.27. Коефіцієнт згасання значно менший за . Тому згасання істотно впливає на залежність n від  лише в області частот  , близьких до  ₀. Для областей, далеких від  ₀, формули (6.54) і (6.55) еквівалентні, бо

.

На явищі нормальної дисперсії (вдалині від резонансної чистоти ₀) ґрунтується робота призмових спектрометрів, за допомогою яких вивчають спектральний склад світла. З іншого боку, поблизу резонансної частоти стають особливо інтенсивними вимушені коливання електронів. Тому в області резонансної частоти спостерігають смугу поглинання (рис. 6.27, пунктирна крива).