Площина

1.Рівняння площини через нормальний вектор і точку.

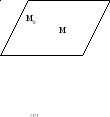
Нехай площина проходить через т.M (x₀,y₀,z₀) ┴ (A,B,C). Знайдемо рівняння площини.

M(x,y,z) і розглянемо вектор

:

(x-x₀;y-y₀;z-z₀)

α ┴; =0;

A(x-x₀)+B(y-y₀)+C(z-z₀)=0, (1)

2.Загальне рівняння площини.

В рівності (1) розкриємо дужки,

-A x₀-B y₀-C z₀=D, Ax+By+Cz+D=0; (2)

а) якщо D=0;А,В,С0,-то площина проходить через початок координат.

б) якщо А=0 – то площина ║ осі ОХ.

в) якщо А=0, D=0 - то площина проходить через вісь ОХ.

г) якщо В=0 – то площина ║ осі ОY.

д) якщо В=0, D=0 - то площина проходить через вісь ОY.

е) якщо С=0 - площина ║ осі ОZ.

є) якщо С=0, D=0 - то площина проходить через вісь ОZ.

ж) якщо А=0, В=0 – то площина ║ площині XOY.

з) якщо В=0, С=0– то площина ║ площині YOZ.

и) якщо А=0, С=0– то площина ║ площині XOZ.

ї) якщо А=0, В=0, D=0 – тоді Z=0 – рівняння площини XOY.

й) якщо В=0, С=0, D=0 – тоді X=0- рівняння площини YOZ.

к) якщо А=0, С=0, D=0– тоді Y=0- рівняння площини XOZ.

3.Рівняння площини через 3 точки.

Нехай площина α визначається точками М₁(x₁,y₁,z₁),M₂(x₂,y₂,z₂),M₃(x₃,y₃,z₃).

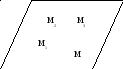
Візьмемо в площині α т.M(x,y,z)

α І розглянемо вектори:

, , .

(x₂-x₁;y₂-y₁;z₂-z₁);

(x₃-x₁;y₃-y₁;z₃-z₁);

(x-x₁;y-y₁;z-z₁ );

Розглянемо їх мішаний добуток: =0, бо вектори компланарні:

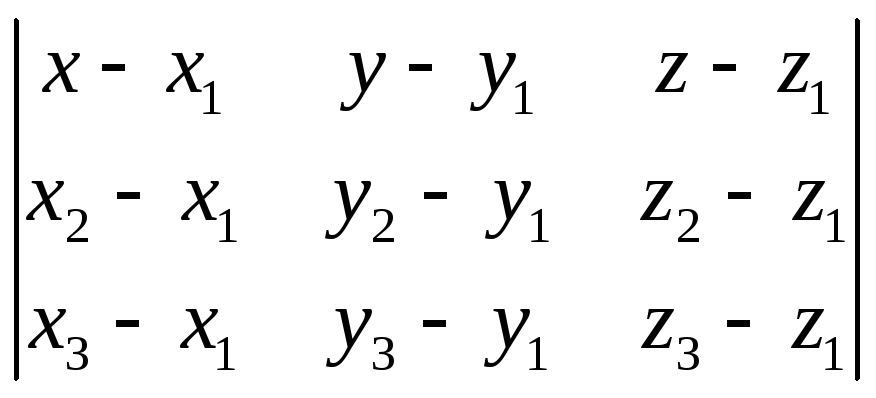(3)

4.Рівняння площини у відрізках на осях координат.

Нехай площина відсікає від осі ОХ відрізок величиною а,- від 0Y – b, від 0Z - c

(4)

5.Кут між площинами.

Нехай площини α₁ і α₂ задані рівняннями:

α₁:A₁x+B₁y+C₁z+D=0;(A₁;B₁;C₁);

α₂: A₂x+B₂y+C₂z+D=0;(A₂;B₂;C₂);

Кут між площинами рівний кутові нормальними векторами:

Cosφ=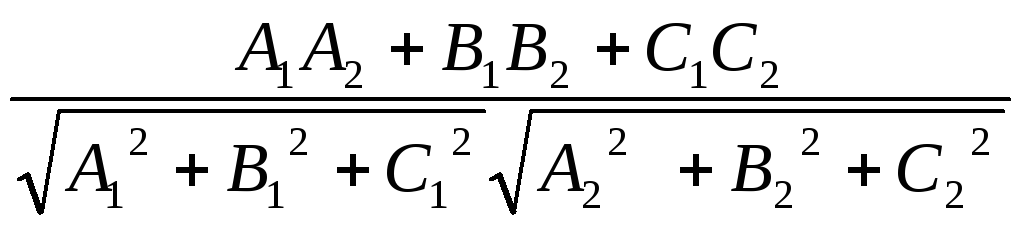; (5)

6.Умови паралельності та перпендикулярності площин.

Площина α₁ ║ площині α₂, якщо ║ =>;

α₁ ┴ α₂, якщо =0,=> А₁А₂+В₁В₂+С₁С₂=0;

Якщо в площинах пропорційні коефіцієнти при їх невідомих на вільні члени, то такі площини співпадають.

7.Відстань від точки до площини.

Знайдемо відстань т.M₀(x₀;y₀;z₀) до площини α, заданої рівнянням Ax+By+Cz+D=0; (A;B;C);

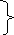
M₀

d

α

Нехай проекцію т.M₀ у площині α є точка М з невідомими координатами(x;y;z), розглянемо вектор :

(x-x₀;y-y₀;z-z₀). Знайдемо скалярний добуток векторів за означенням: =cosφ=d;

φ:0;180⁰; cos0=1; cos180= -1;

Розглянемо скалярний добуток цих векторів в координатній формі:

=А(x-x₀)+В(y-y₀)+С(z-z₀)=Ax+By+Cz-A x₀-B y₀-C z₀+-(A x₀+B y₀+C z₀+D); Ax+By+Cz=-D;

Прирівняємо скалярні добутки по модулю:=d;

D=; (7)

Наприклад: знайти відстань між паралельними площинами:

α₁:x-2y+2z+5=0;

α₂:2x-4y+4z-7=0;

n₁(1;-2;2);

візьмемо довільну точку, що є площині α₂, М₀(;0;0);

Знайдемо відстань т. М₀ до площини α₁:

D====2=2(лін.од.)