
- •Лінійна алгебра та аналітична геометрія
- •I Елементи лінійної алгебри
- •Визначники, їх обчислення та властивості
- •Визначником 3-го порядку – називається число, яке ставиться у відповідність матриці розмірами (3х3) за таким законом:
- •Дослідження систем за допомогою рангів
- •Іі Елементи векторної алгебри
- •Базис. Прямокутна система координат.
- •Розклад вектора за базисними векторами.
- •Лінійні операції над векторами заданими координатами.
- •Напрямні косинуси вектора
- •Скалярний добуток векторів
- •Скалярний добуток в координатах
- •Застосування скалярного добутку
- •Векторний добуток векторів
- •Властивості векторного добутку
- •Векторний добуток в координатах
- •Застосування векторного добутку
- •Мішаний добуток векторів
- •Мішаний добуток в координатах
- •Застосування мішаного добутку
- •III Аналітична геометрія
- •Дослідження загального рівняння
- •Площина
- •1.Рівняння площини через нормальний вектор і точку.
- •2.Загальне рівняння площини.
- •6.Умови паралельності та перпендикулярності площин.
- •Пряма в просторі
- •4.Загальне рівняння прямої.
- •Кут між прямими в просторі
- •Взаємне розміщення прямої та площини в просторі
- •Лінії другого порядку.
- •4. Парабола
- •Поверхні другого порядку
Скалярний добуток векторів
Скалярним
добутком
двох
векторів
![]() називається число, яке дорівнює добутку
модулів цих векторів на косинус кута
між ними:
називається число, яке дорівнює добутку
модулів цих векторів на косинус кута
між ними:
![]() , де
, де
![]() -
кут між векторами
-
кут між векторами
![]()
Механічний зміст скалярного добутку.
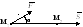
Якщо
матеріальна точка під дією сили
![]() переміщається з положення М1
в положення М2
( вектор переміщення
переміщається з положення М1
в положення М2
( вектор переміщення![]() ,
то робота виконана при цьому дорівнює
,
то робота виконана при цьому дорівнює
![]()
Властивості скалярного добутку
1)
При зміні векторів місцями, скалярний
добуток не змінюється
![]()
2)
Скалярний множник можна виносити за
знак скалярного добутку
![]() ,
,
![]()
3)
![]()
4) Скалярний добуток векторів дорівнює добуткові одного із модулів векторів на проекцію другого на попередній:
![]()
![]()
![]()
5) Скалярний квадрат вектора дорівнює квадрату його модуля.
![]() ;
;
![]()
6) Якщо вектори взаємно перпендикулярні, то їх скалярний добуток дорівнює нулю:
![]() .
.
7)
Якщо α – гострий кут між векторами, то
![]() - додатне число, якщо α – тупий кут, то
- додатне число, якщо α – тупий кут, то
![]() - від’ємне число.
- від’ємне число.
Зауваження : Оскільки властивість 6 є і достатньою умовою, то вона служить критерієм перевірки перпендикулярності ненульових векторів.
Скалярний добуток в координатах
Нехай
вектори
![]() і
і
![]() задані
координатами:
задані
координатами:
![]()
![]()
Знайдемо
![]() .
.
![]()
![]()
Так
як
![]() ,
,
![]() =1,
=1,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
![]() .
.
Застосування скалярного добутку
-
Робота виконана силою
 по переміщенні матеріальної точки
вздовж вектора
по переміщенні матеріальної точки
вздовж вектора
 :
:
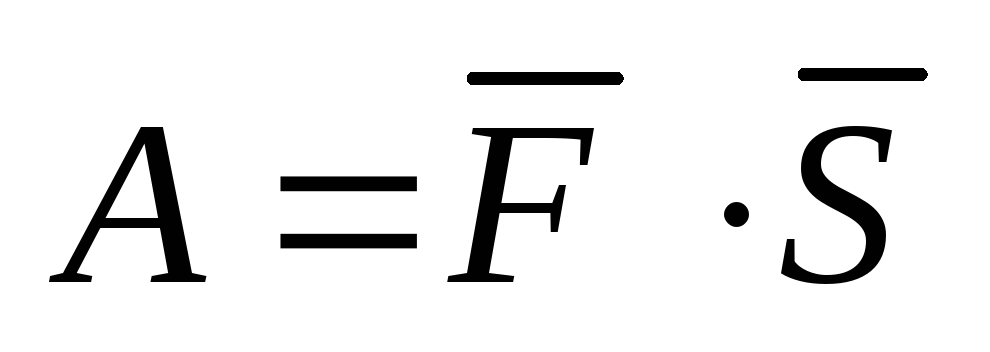
-
Проекція вектора на вектор:
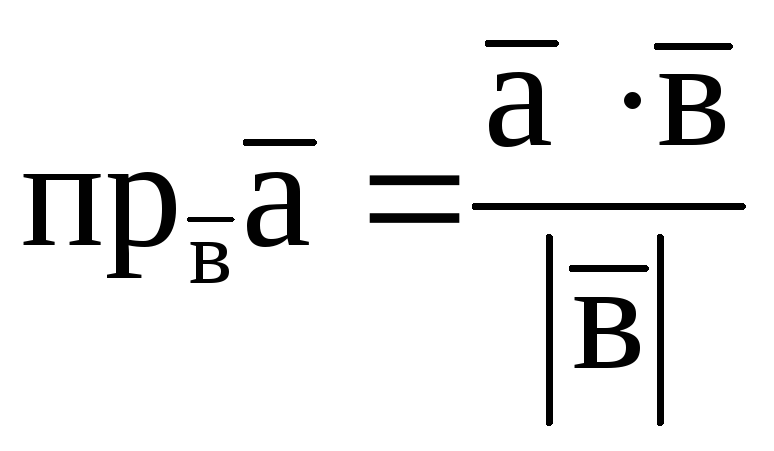 ;
;
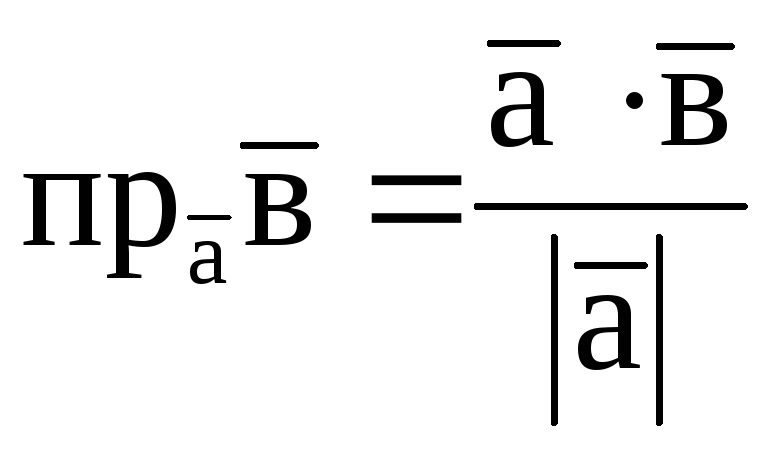 .
. -
Якщо
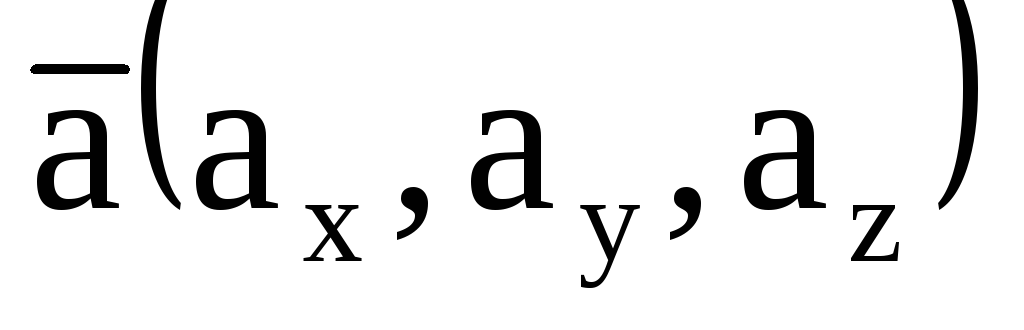 ,
то
,
то
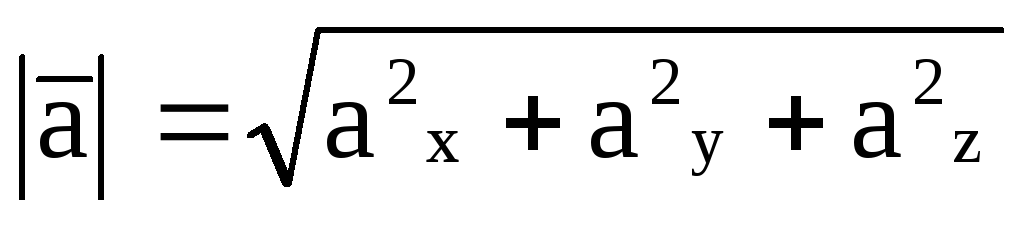 .
. -
Якщо для двох ненульових векторів
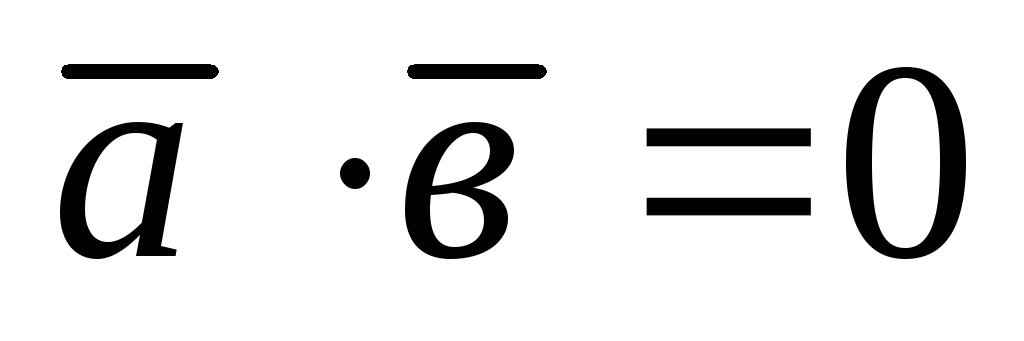 ,
то
,
то
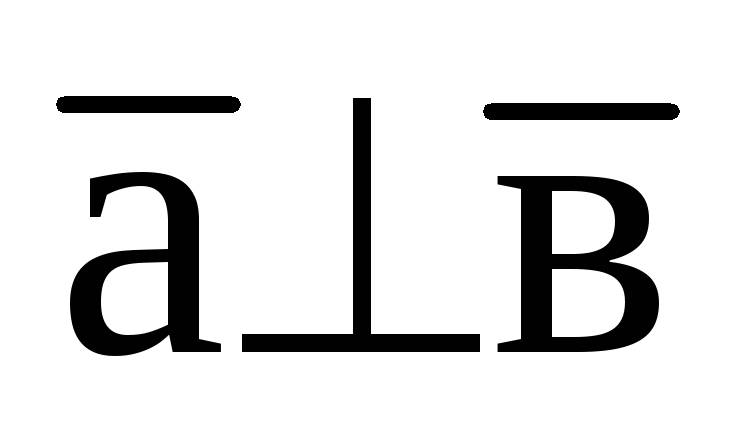 .
. -
Кут між векторами
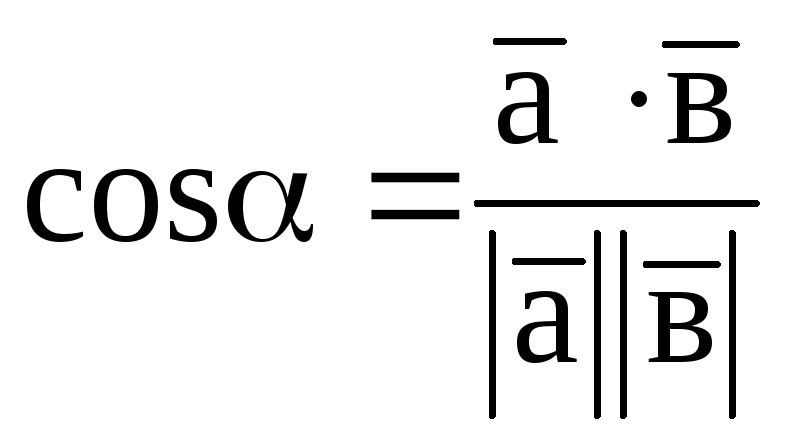 .
.
Векторний добуток векторів
Означення
1. Трійка векторів
![]() називається правою,
якщо з кінця вектора
називається правою,
якщо з кінця вектора
![]() видно, що найменший поворот від
видно, що найменший поворот від
![]() до
до
![]() здійснюється проти годинникової
стрілки.
здійснюється проти годинникової
стрілки.

Означення
2. Трійка векторів називається лівою,
якщо кінця вектора
![]() видно найменший поворот від
видно найменший поворот від
![]() до
до
![]() здійснюється за годинниковою стрілкою.
здійснюється за годинниковою стрілкою.

Означення
3. Векторним
добутком векторів
![]() і
і
![]() називається такий вектор
називається такий вектор
![]() ,
перпендикулярний до векторів
,
перпендикулярний до векторів
![]() і
і
![]() ,
який утворює з ними праву трійку, а
модуль його дорівнює:
,
який утворює з ними праву трійку, а
модуль його дорівнює:
![]() ,
де
,
де
![]() .
.
Фізичний
зміст
векторного добутку: якщо тверде тіло,
закріплене до осі в точці О, рухається
навколо неї під дією прикладенї сили
в точці А, то момент сили
![]() ,
де
,
де
![]() - плече сили.
- плече сили.
Властивості векторного добутку
-
При зміні векторів місцями векторний добуток змінює знак на протилежний:
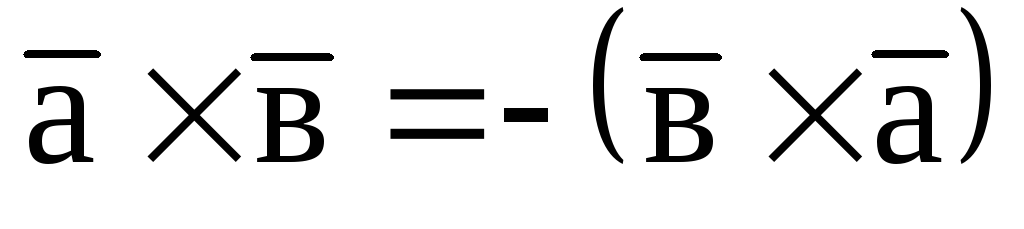 ,
бо міняється трійка векторів.
,
бо міняється трійка векторів. -
Скалярний множник можна винести за знак векторного добутку:
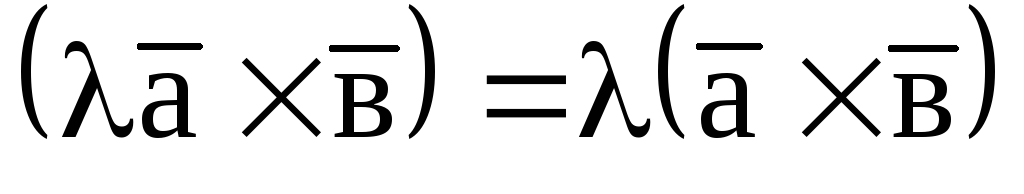 ;
;
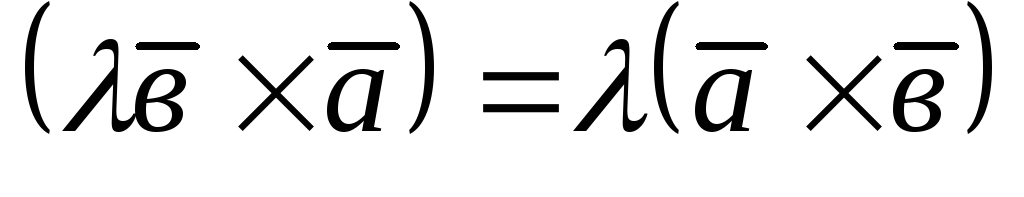
-
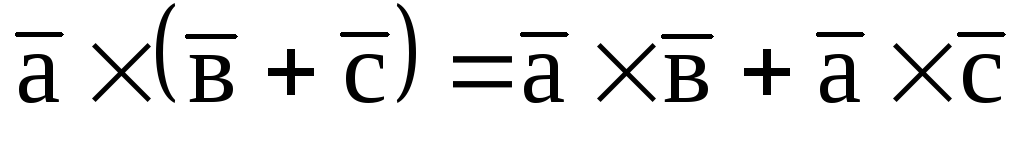
-
Якщо вектори колінеарні, то векторний добуток дорівнює 0.
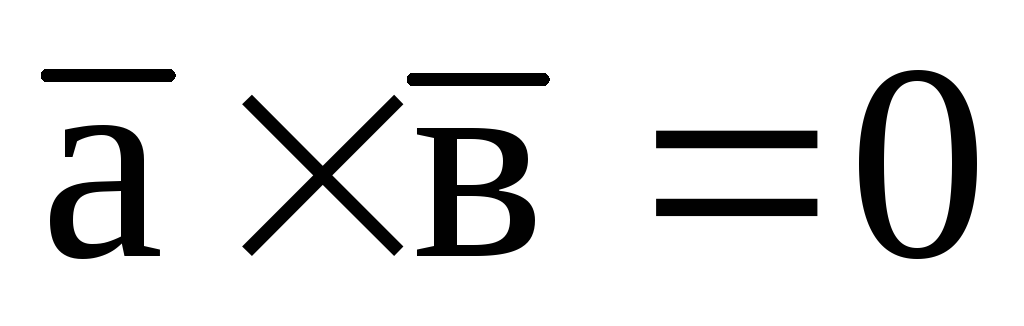
Зауваження:
Властивість 4 являється і достатньою
умовою колінеарності векторів, тобто,
якщо![]() ,
то вектори колінеарні
,
то вектори колінеарні
Векторний добуток в координатах
Нехай![]() і
і
![]() задані координатами:
задані координатами:
Знайдемо
![]() .
.
![]()
![]()
Так
як
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
то
,
то
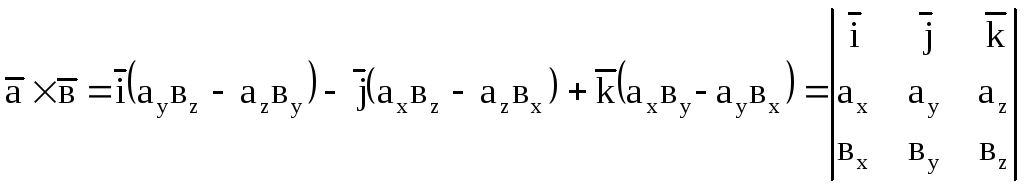 .
.
Отже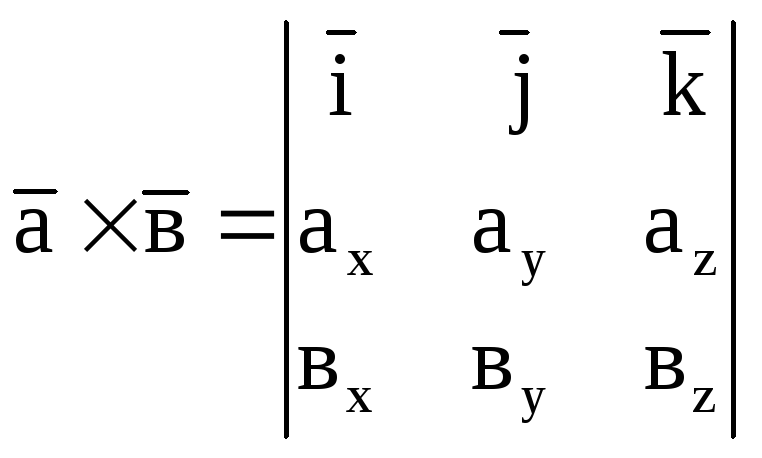 .
.
