
- •Лінійна алгебра та аналітична геометрія
- •I Елементи лінійної алгебри
- •Визначники, їх обчислення та властивості
- •Визначником 3-го порядку – називається число, яке ставиться у відповідність матриці розмірами (3х3) за таким законом:
- •Дослідження систем за допомогою рангів
- •Іі Елементи векторної алгебри
- •Базис. Прямокутна система координат.
- •Розклад вектора за базисними векторами.
- •Лінійні операції над векторами заданими координатами.
- •Напрямні косинуси вектора
- •Скалярний добуток векторів
- •Скалярний добуток в координатах
- •Застосування скалярного добутку
- •Векторний добуток векторів
- •Властивості векторного добутку
- •Векторний добуток в координатах
- •Застосування векторного добутку
- •Мішаний добуток векторів
- •Мішаний добуток в координатах
- •Застосування мішаного добутку
- •III Аналітична геометрія
- •Дослідження загального рівняння
- •Площина
- •1.Рівняння площини через нормальний вектор і точку.
- •2.Загальне рівняння площини.
- •6.Умови паралельності та перпендикулярності площин.
- •Пряма в просторі
- •4.Загальне рівняння прямої.
- •Кут між прямими в просторі
- •Взаємне розміщення прямої та площини в просторі
- •Лінії другого порядку.
- •4. Парабола
- •Поверхні другого порядку
Дослідження систем за допомогою рангів
Мінором k-го порядку називається визначник, утворений з k рядків і k стовпчиків даної матриці.
Наприклад: знайти мінори матриці
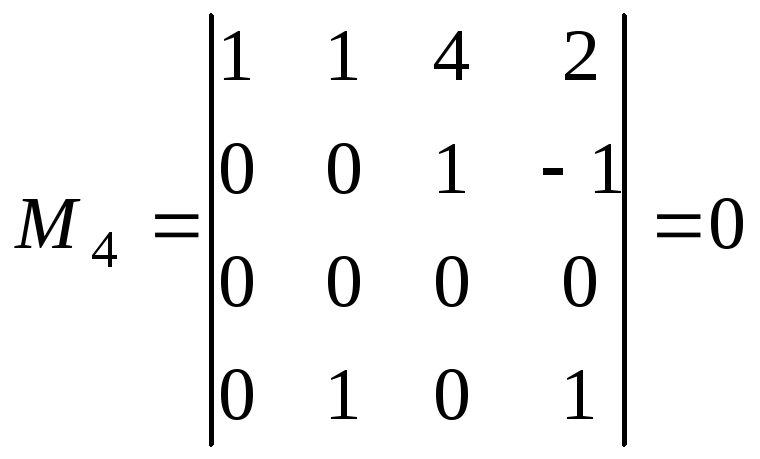
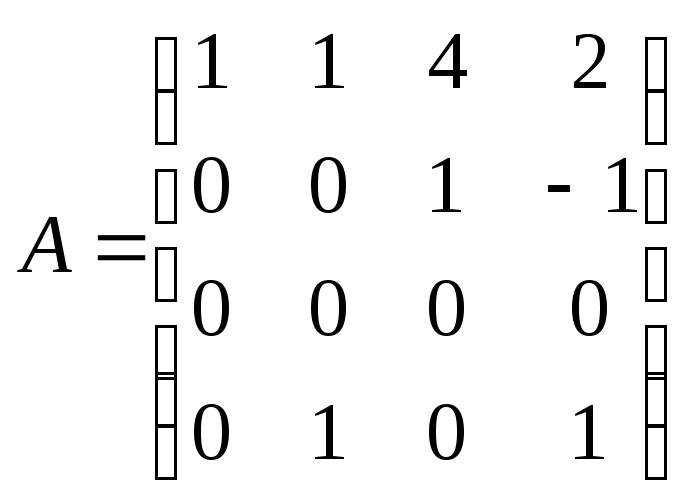
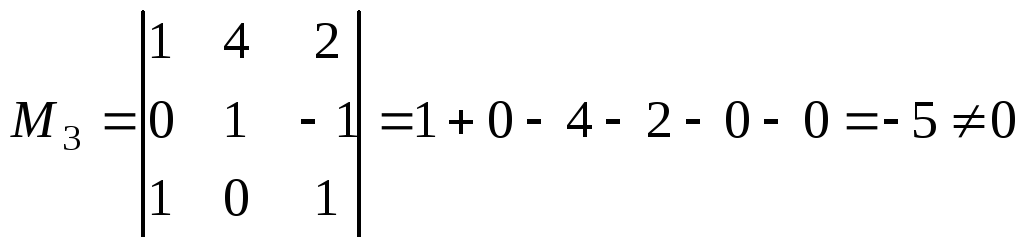 Найвищий
порядок мінора, відмінного від нуля,
називається рангом
матриці
r(A)=3.
Найвищий
порядок мінора, відмінного від нуля,
називається рангом
матриці
r(A)=3.
Розглянемо
систему рівнянь (1) для якої матриця А
– це матриця задана з коефіцієнтів при
невідомих, а матриця
![]() - розширена матриця до матриці А, яка
складається з коефіцієнтів при невідомих
та вільних членів.
- розширена матриця до матриці А, яка
складається з коефіцієнтів при невідомих
та вільних членів.
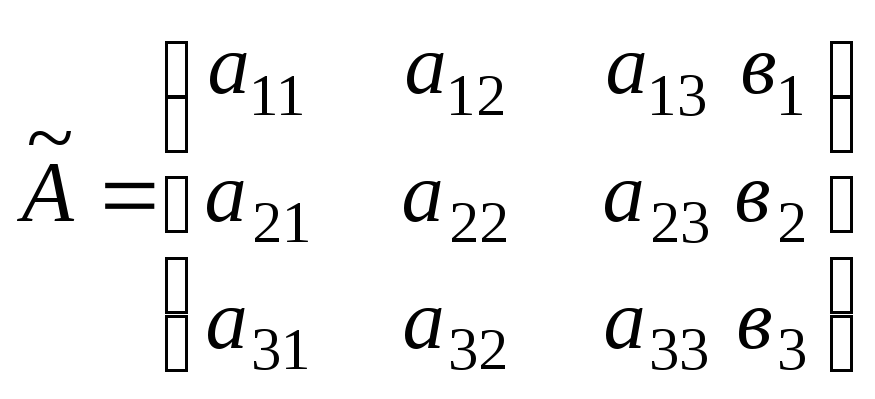
1).
Теорема Кронекера-Капеллі: якщо ранг
матриці А дорівнює рангу розширеної
матриці
![]() і дорівнює числу невідомих, r(A)=r(
і дорівнює числу невідомих, r(A)=r(![]() )=n,
то система має єдиний розв’язок.
)=n,
то система має єдиний розв’язок.
2).
Якщо ранг матриці А дорівнює рангу
розширеної матриці
![]() r(A)
r(A)
![]() r(
r(![]() ).
,то система не має розв’язку:
).
,то система не має розв’язку:
3).
Якщо ранг А дорівнює рангу розширеної
![]() ,
але менше числа невідомих, r(A)=r(
,
але менше числа невідомих, r(A)=r(![]() )
< n
)
< n
то система має безліч розв’язків.
Іі Елементи векторної алгебри
Предметом вивчення цього розділу вищої математики є вектори, дії над ними та їх застосування.
Вектор – напрямний відрізок.
Вектор
позначається однієї малою буквою
латинського алфавіту із стрілкою зверху
або символом
![]() ,
де т. А – початок, а т. В – кінець вектора.
,
де т. А – початок, а т. В – кінець вектора.
Довжиною
або
модулем
вектора
![]() називається довжина відрізка АВ.
Позначається вона символом
називається довжина відрізка АВ.
Позначається вона символом
![]() ..
..
Вектор
називають нульовим,
якщо початок і кінець його збігаються.
Позначають нульовий вектор символом
![]() .
.
Вектор,
довжина якого дорівнює одиниці,
називається одиничним. Такий вектор
позначається
![]()
Вектори, що мають одинакові напрямки, називають співнапрямленими, а вектори, що мають протилежні напрямки – протилежнонапрямленими.
Вектори, що лежать в паралельних площинах, або в одній площини називаються компланарними.
Вектори називаються колінеарними, якщо вони лежать на паралельних прямих або на одній прямій.
Два вектори називаються рівними, якщо вони колінеарні, співнаправлені і мають однакову довжину.
Два колінеарні вектори, Які мають однакову довжину і протилежно напрямлені, називаються взаємно протилежними.
Над векторами можна виконувати лінійні операції : додавати, віднімати, множити вектор на число.
Якщо
вектори задані направленими відрізками
то : сумою
двох векторів
![]() і
і
![]() ,
відкладених послідовно, є вектор
,
відкладених послідовно, є вектор
![]() .
Який сполучає початок першого з кінцем
другого. Правило суми двох векторів
узагальнюються на суму кількох векторів
.
Який сполучає початок першого з кінцем
другого. Правило суми двох векторів
узагальнюються на суму кількох векторів
Геометрично вектори можна додавати за правилом трикутника або паралелограма:
а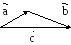 )
правило трикутника; б)правило
паралелограма
)
правило трикутника; б)правило
паралелограма

![]() +
+![]() =
=![]()
![]() +
+![]() =
=![]()
Різницею
двох векторів
![]() і
і
![]() називається такий вектор
називається такий вектор
![]() ,
який в сумі з вектором
,
який в сумі з вектором
![]() дає вектор
дає вектор
![]() :
:
![]() ,
,
![]()
Різницею
двох векторів
![]() і
і
![]() ,
що виходять з однієї точки, є вектор,
який сполучає кінці цих векторів і
направлений в сторону того вектора,
від якого віднімаємо:
,
що виходять з однієї точки, є вектор,
який сполучає кінці цих векторів і
направлений в сторону того вектора,
від якого віднімаємо:
![]()
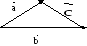
Геометрично
різницю векторів можна знаходити за
правилом паралелограма:
![]()
Добутком
вектора
![]() на число
на число
![]() є вектор, співнаправний з вектором
є вектор, співнаправний з вектором
![]() ,
якщо
,
якщо
![]() - число додатне, протилежно направлений
з вектором
- число додатне, протилежно направлений
з вектором
![]() ,
якщо
,
якщо
![]() - від’ємне число. Модуль даного вектора
дорівнює
- від’ємне число. Модуль даного вектора
дорівнює
![]() ,
причому якщо
,
причому якщо
![]() ,
то довжина вектора зменшується, а якщо
,
то довжина вектора зменшується, а якщо
![]() ,то
довжина вектора збільшується.
,то
довжина вектора збільшується.
Операції додавання і множення вектора на число мають такі властивості:
-
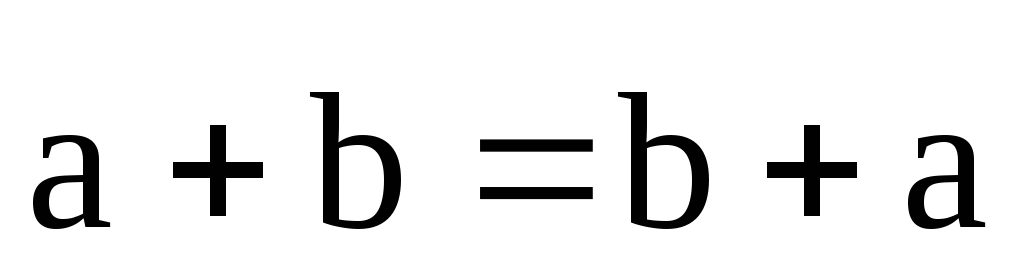 ;
5.
;
5.
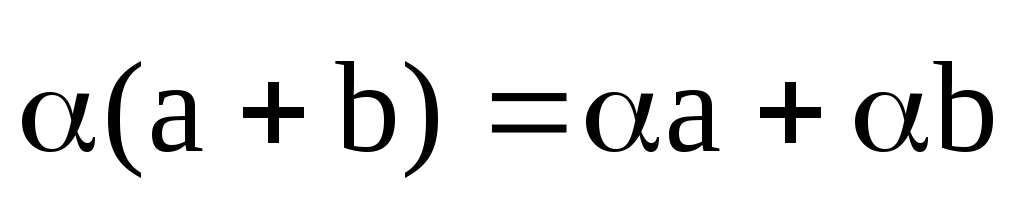 ;
; -
(
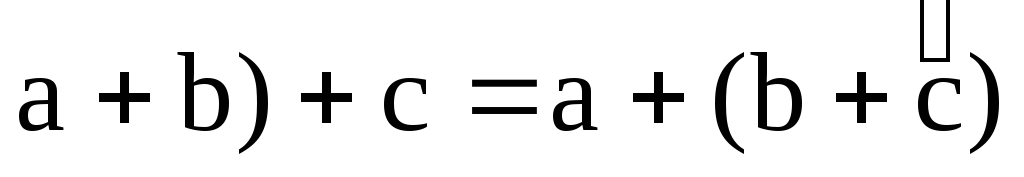 ;
6.
;
6.
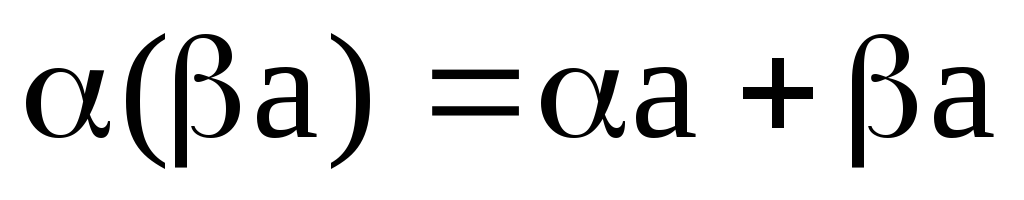 ;
; -
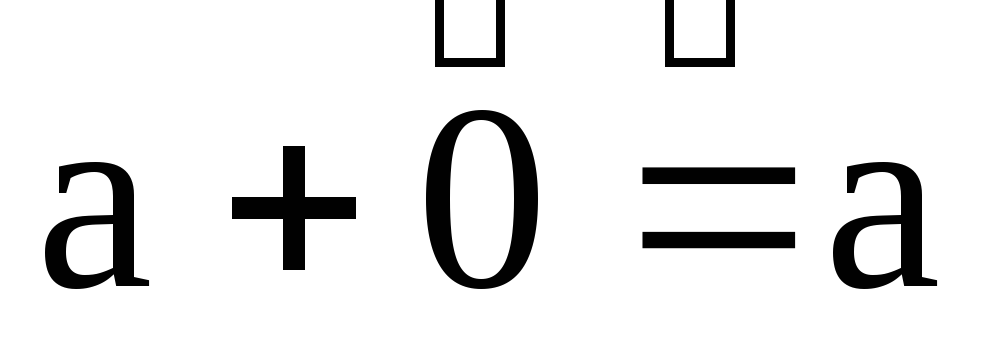 ;
7. (
;
7. (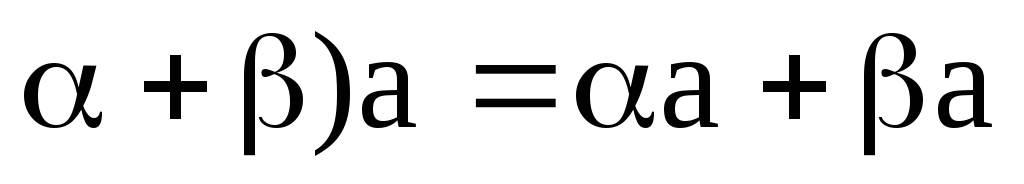 ;
; -
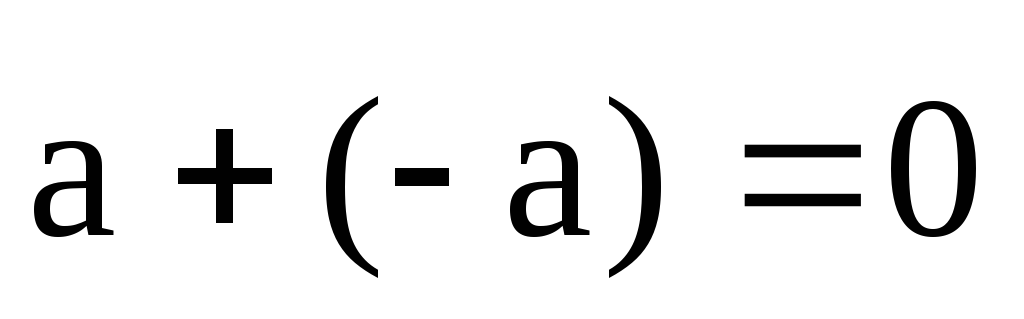 ;
8. 1
;
8. 1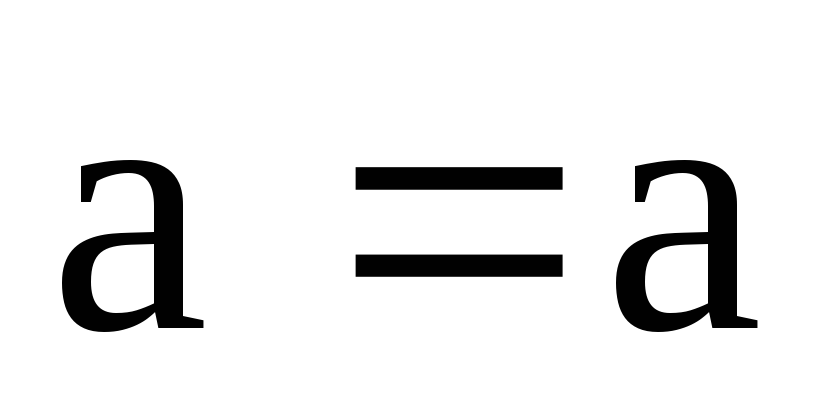 .
.
