Свойства бинарных отношений

Пусть задано на множестве , .

1. Рефлексивность: .

Отношение  на множестве X называется рефлексивным, если для любого имеет место , то есть каждый элемент находится в отношении  к самому себе.

Матрица рефлексивного отношения имеет единичную главную диагональ, а граф рефлексивного отношения – имеет петлю возле каждого своего элемента.

Например:

,

,

,

.

На множестве людей: “быть родственником”, ”обучаться в одной студенческой группе ”.

На множестве множеств: A  B, A=B.

2. Антирефлексивность: .

Отношение  на множестве X называется антирефлексивным, если не существует хХ такого, что имеет место хх, то есть ни один элемент не находится в отношении  к самому себе.

Матрица антирефлексивного отношения имеет нулевую главную диагональ, а граф – не имеет ни одной петли.

Например:

,

,

.

На множестве людей: “быть родителем”, ”быть ребенком”.

На множестве множеств: A  B, AB.

3. Нерефлексивность: .

4. Симметричность: .

Отношение  на множестве X называется cимметричным, если для всех х и y из Х, из принадлежности (x,y) отношению  следует, что и (y,x) принадлежит отношению .

Матрица симметричного отношения симметрична относительно главной диагонали, а граф – для каждой дуги (x,y) существует обратная дуга (y,x).

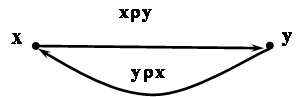
Например:

,

,

.

На множестве людей: “быть родственником”, ”обучаться в одной студенческой группе ”.

Отношение " брат " является симметричным на множестве мужчин и не является симметричным на множестве всех людей.

На множестве множеств: , .

5. Антисимметричность: .

Отношение  на множестве X называется антиcимметричным, если для всех х и y из Х, из принадлежности (x,y) и (y,x) отношению  следует, что .

Матрица антисимметричного отношения не имеет ни одной симметричной единицы относительно главной диагонали, а граф – для каждой дуги (x,y) не существует обратная дуга (y,x) и наоборот.

Свойства симметричности и антисимметричности не являются взаимоисключающими, примером может служить отношения равенства на множестве натуральных чисел.

Например:

,

,

,

,

.

На множестве людей: “быть выше”, ”быть равным”.

На множестве множеств: , , .

6. Транзитивность: .

Отношение  на множестве X называется транзитивным, если для всех х,y,z из Х, из принадлежности (x,y) и (y,z) отношению  следует, что (x,z) также принадлежит .

Например:

,

,

,

,

,

.

На множестве людей: “быть выше”, ”обучаться в одной студенческой группе”.

На множестве множеств: , , .

Отношение r на множестве X не является транзитивным, если существует хотя бы один пример того, что для некоторых х,y,z множества Х из принадлежности (x,y) и (y,z) отношению r не следует, что (x,z) также принадлежит r.

Например.

1) .

Отношение не является транзитивным, потому что из принадлежности этому отношению пар и , не следует, что и пара принадлежит отношению .

2) Пусть задано двухэлементное множество определим все бинарные отношения на этом множестве:

.

Для всех отношений, заданных на множестве , определить наличие или отсутствие свойств: рефлексивность, антирефлексивность, симметричность и антисимметричность, транзитивность.

Введем следующие обозначения:

а) рефлексивность – Р;

б) антирефлексивность – АР;

в) симметричность – С;

г) антисимметричность – АС;

д) транзитивность – Т.

№		Р	АР	С	АС	Т
1		-	+	+	+	+
2		-	-	+	+	+
3		-	+	-	+	+
4		-	+	-	+	+
5		-	-	+	+	+
6		-	-	-	+	+
7		-	-	-	+	+
8		+	-	+	+	+
9		-	+	+	-	-
10		-	-	-	+	+
11		-	-	-	+	+
12		-	-	+	-	-
13		+	-	-	+	+
14		+	-	-	+	+
15		-	-	+	-	-
16		+	-	+	-	+

Отношение порядка – антисимметрично, транзитивно.

Отношение нестрого порядка () – рефлексивно, антисимметрично, транзитивно.

,

.

На множестве множеств: , .

Отношение строгого порядка () – антирефлексивно, антисимметрично, транзитивно.

,

.

На множестве множеств: “”.

- “x предшествует y в смысле отношения строгого порядка”,

- “x предшествует y в смысле отношения нестрогого порядка”.

Два элемента и некоторого упорядоченного множества (множества, на котором существует отношение порядка) сравнимы между собой, если предшествует , и/или предшествует в смысле отношения порядка.

Если в упорядоченном множестве существует пара элементов x и y, для которой ни не предшествует , ни не предшествует , тогда говорят, что эти два элемента не сравнимы между собой в смысле этого.

В отношениях полного порядка все элементы сравнимы между собой, а в отношениях частичного порядка не все элементы сравнимы между собой.

Например:

Отношения полного порядка:

,

.

Отношения частичного порядка:

,

,

на множестве множеств:

,

,

.

Отношение эквивалентности (  ) – рефлексивно, симметрично, транзитивно.

Класс эквивалентности для х: .

Например:

,

r= { (x, y) | x=y(mod m), x,y Î N }.

На множестве людей: “иметь одно имя”, ”обучаться в одной студенческой группе”.

На множестве множеств: .

Отношение эквивалентности разбивает – множество, на котором задано отношение на непересекающиеся, которые называют классами эквивалентности.

Элементы, принадлежащие одному классу, находятся между собой в отношении эквивалентности, элементы из разных классов в отношении эквивалентности между собой не находятся.

Например:

Отношение задано на множестве списком пар

.

Область определения: .

Область значений: .

Отношение – рефлексивно, симметрично, транзитивно, следовательно, это отношение эквивалентности.

Классы эквивалентности:

.

Например:

Отношение .

Это отношение называют отношением сравнения по модулю на множестве натуральных чисел.

означает, что и имеют одинаковый остаток при делении на .

Отрезок натурального ряда .

Отношение сравнения по модулю 3 на :

.

Область определения и область значений: .

Отношение – рефлексивно, симметрично, транзитивно.

Отношение – отношение эквивалентности.

Классы эквивалентности: .

Пусть – некоторое бинарное отношение.

Обратным отношением называется отношение, которое определяется следующим образом:

Обратное отношение получается путём перестановки значений в парах исходного отношения.

Пусть и – произвольные бинарные отношения такие, что где X, Y, Z – некоторые множества.

Композиция отношений и – это таке бинарное отношение которое состоит из упорядоченных пар для которых существует такой элемент, что выполняются условия:

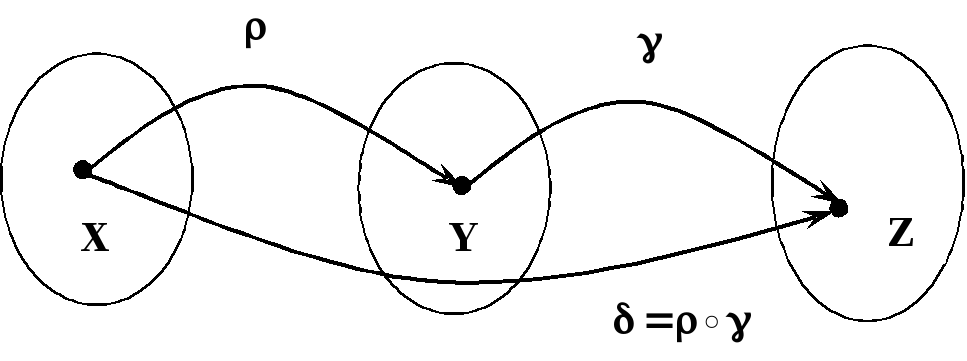
Например.

.

.

.

.