Пункты решения задачи о минимизации фал
1. Построение сокращенной ДНФ для заданной функции.
2. Удаление из СДНФ "лишних" максимальных интервалов.
Например.
1) ФАЛ задана множеством
.
Найти ДСНФ, СДНФ та МДНФ.
Решение.
ДДНФ
,
R=12.
СДНФ=МДНФ
,
R=7.
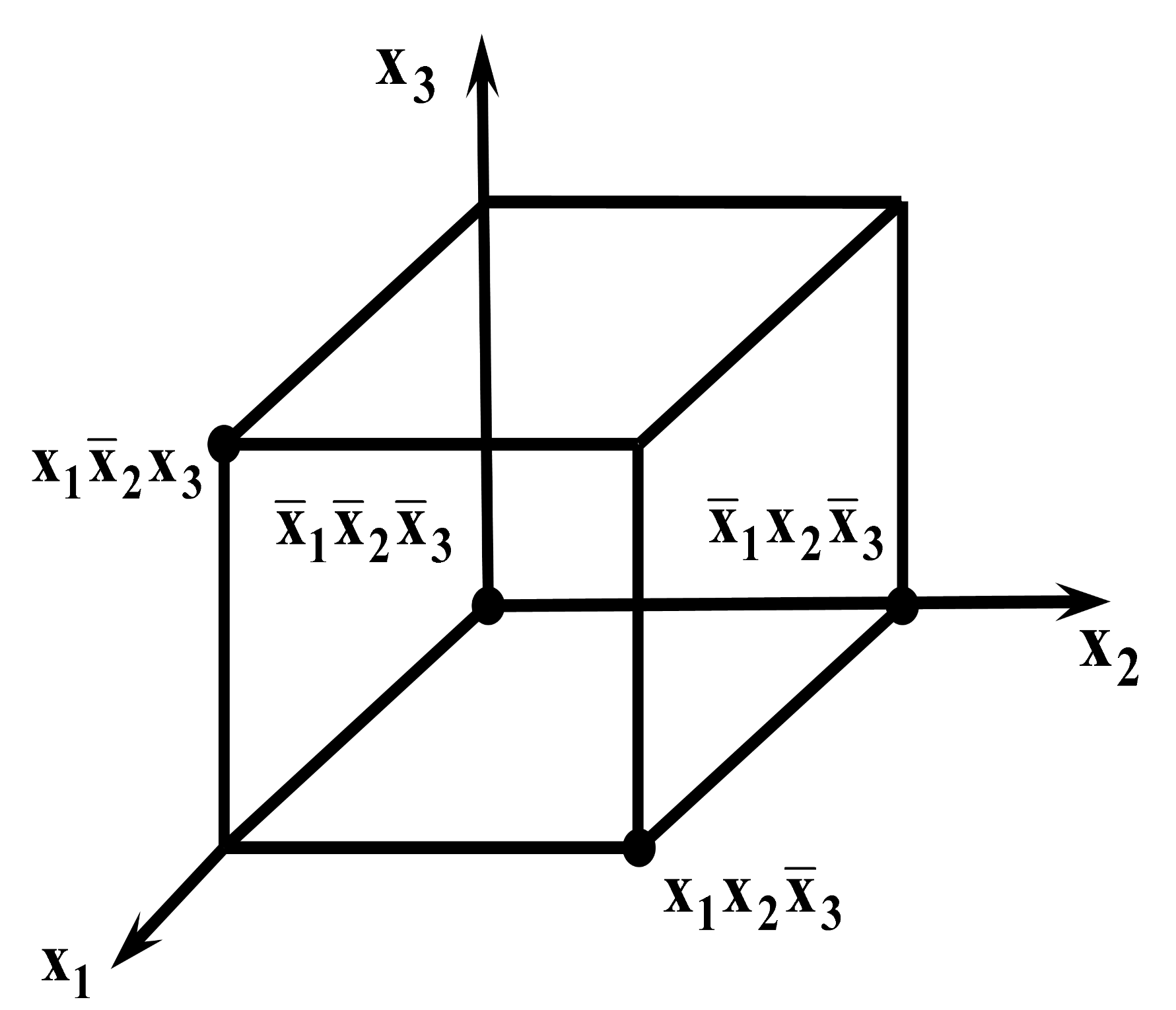
2) ФАЛ задана множеством
.
Найти ДСНФ,
СДНФ и МДНФ.
Решение.
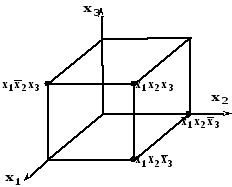
ДСНФ
,
.
СДНФ
,
.
МДНФ
,
.
3) ФАЛ задана множеством
.
Найти ДСНФ,
СДНФ и МДНФ.
Решение.
ДСНФ
,
.
СДНФ
,
.
МДНФ1
,
.
МДНФ2
,
.
Минимальная
форма определяется
неоднозначно, то есть
может существовать несколько различных
минимальных форм. В
данном случае ФАЛ
имеет две разные минимальные
дизъюнктивные нормальные формы,
очевидно, что суммарный
ранг у них одинаковый
и равен
.
Метод Квайна минимизации булевых функций
Предположим, что функция задана в ДСНФ.
Элементарные конъюнкции ранга n будем называть минитермами ранга n.
Шаг 1. Нахождение первичных импликант.
Все минитермы данной ФАЛ сравниваются между собой попарно.
Если минитермы
mi
и mj таковы, что их можно попарно
представить в виде
,
то выписывается конъюнкция, которая
является минитермом ранга n-1:
.
Минитермы n-го ранга, для которых произошло склеивание отмечаются (*).
После построения всех минитермов (n-1)-го ранга вновь сравнивают их попарно, выписывают минитермы (n-2)-го ранга и отмечают склеивающиеся минитермы и т.д.
Этап заканчивается, когда вновь полученные минитермы l-го ранга уже не склеиваются между собой.
Все неотмеченные минитермы называются первичными или простыми импликантами.
Шаг 2. Расстановка меток.
Для данной функции
,
где
- первичные импликанты. (1)
Соотношение (1) определяет СДНФ для данной функции.
Для нахождения минимального покрытия интервалами максимального ранга необходимо произвести выбрасывание некоторого количества первичных импликант.
На этапе расстановки меток составляется таблица, число строк в которой равно числу первичных импликант, число столбцов равно числу минитермов ДСНФ.
Если в минитерм ДСНФ входит какой-либо из первичных импликант, то на пересечении соответствующего столбца и строки ставим метку.
Шаг 3. Нахождение существенных импликант.
Если в столбце стоит всего одна метка, то соответствующая импликанта – существенная.
Существенная импликанта не может быть
исключена из правой части (1), т.к. без
нее не будет получено покрытие всего
множества
данной функции. Поэтому из таблицы меток
исключаем строки, соответствующие
существенным импликантам, и столбцы
минитермов, покрываемых ими.
Шаг 4. Вычеркивание лишних столбцов.
Если в таблице есть два столбца с метками в одинаковых строках, то один из них вычеркивается (так как покрытие одного обеспечивает и покрытие другого).
Шаг 5. Вычеркивание лишних первичных импликант.
Если после этапа 4 в таблице есть строки без единой метки, то они вычеркиваются.
Шаг 6. Выбор минимального покрытия максимальными интервалами.
Исследуется полученная таблица: выбирается такая совокупность первичных импликант, которая включает метки во всех столбцах (по крайней мере по 1 в каждом столбце).
При нескольких вариантах отдается предпочтение варианту покрытия с минимальным суммарным числом букв в простых импликантах.