2.1.7 Параметрическое и каноническое уравнения прямой

Пусть прямая l задана начальной точкой М₀ (х₀; у₀) и направляющим вектором (а₁;а₂),. Пусть т. М(х ; у) – любая точка, лежащая на прямой l . Тогда вектор коллинеарен вектору . Следовательно, = . Записывая это уравнение в координатах, получаем параметрическое уравнение прямой

(8)

Исключим параметр t из уравнения (9). Это возможно, так как вектор , и потому хотя бы одна из его координат отлична от нуля.

Пусть и , тогда , и, следовательно,

27

= . (9)

Уравнение (9) называется каноническим уравнением прямой с направляющим вектором

=(а₁; а₂). Если а₁ =0 и , то уравнения (8) примут вид

.

Этими уравнениями задается прямая, параллельная оси Оу и проходящая через точку

М₀ (х₀; у₀). Каноническое уравнение такой прямой имеет вид

х=х₀ (10)

Если , , то уравнения (8) примут вид

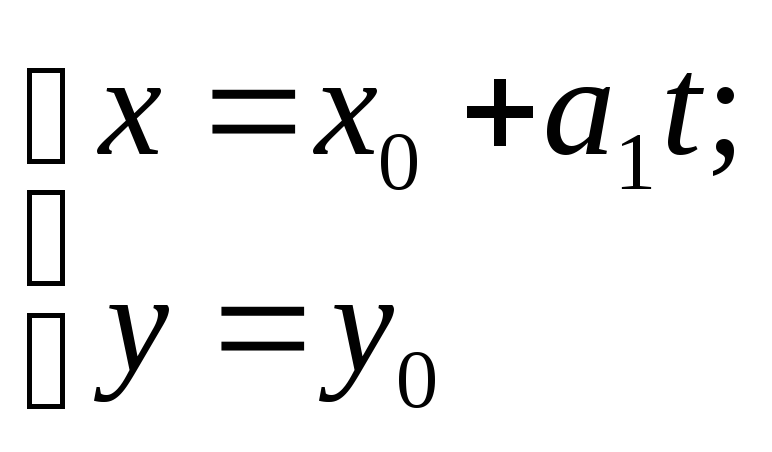
Этими уравнениями задается прямая, параллельная оси Ох и проходящая через точку

М₀ (х₀; у₀). Каноническое уравнение такой прямой имеет вид

у=у₀ (11)

2.1.8 Угол между прямыми. Условие параллельности и перпендикулярности двух прямых

Пусть даны две прямые, заданные общими уравнениями:

и

Тогда угол φ между ними определяется по формуле:

(12)

Пример 10. Вычислить угол между прямыми и .

Решение: ; .

Условие параллельности 2-х прямых: (13)

Условие перпендикулярности 2-х прямых: (14)

Пример 11. Выяснить взаимное расположение прямых:

Решение: а) ;

б)

Если прямые заданы уравнениями с угловыми коэффициентами:

то угол φ между ними вычисляется по формулам

или (15)

28

Пример 12. Вычислить угол между прямыми

Решение:

Условие параллельности в этом случае имеет вид: (16)

Условие перпендикулярности прямых: (17)

Пример 13. Выяснить взаимное расположение прямых:

Решение:

Если две прямые заданы каноническими уравнениями:

и

то угол φ между этими прямыми определяется по формуле:

(18)

Пример: найти угол между прямыми и .

Решение: .

Условие параллельности прямых: (19)

Условие перпендикулярности прямых: (20)

Пример: выяснить взаимное расположение прямых:

а) и ;

б) и .

Решение: а) - прямые параллельны;

б) - значит, прямые перпендикулярны.