Задача 2. Вычисление определенного интеграла

Написать программу для вычисления определенного интеграла как функции параметра с.

Комментарии

Для вычисления интеграла в данной задаче допустима любая из квадратурных формул Ньютона - Котеса: прямоугольников, трапеций, Симпсона и т.п. [1]. Согласно этим формулам, искомый интеграл можно приближенно представить следующим образом:

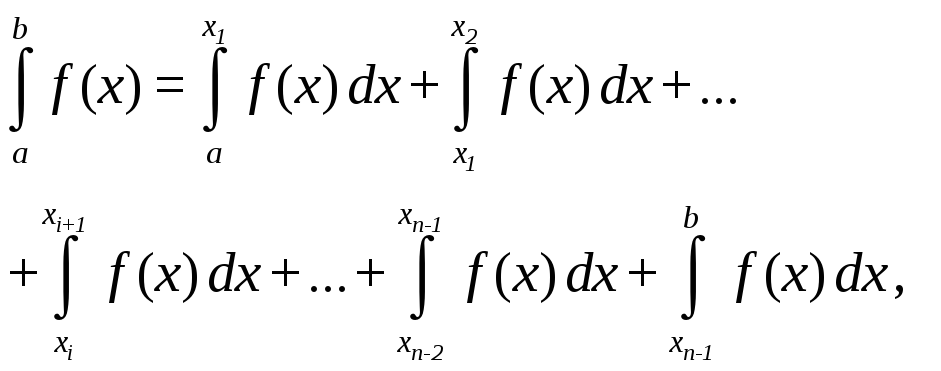
где. При этом

– формула прямоугольников;

– формула трапеций;

– формула Симпсона. При решении данной задачи можно разбивать отрезок [a,b] на равные отрезки [x_i,x_i+1].

Методические указания

Точность получаемого результата проверить,

а) увеличивая в несколько раз число отрезков, на которые делится отрезок [a,b];

б) сопоставляя численный и аналитический результат для тестового варианта расчета – интегрирования полинома – и принимая во внимание, что с помощью формул прямоугольников и трапеций точно интегрируется линейная функция, а с помощью формулы Симпсона – произвольный полином третьей степени [1].

Таблица 2

Подынтегральные функции, пределы интегрирования и величина интеграла при некоторых значениях параметра

№ вар.				Значение при данном
1		2 1	1 2	-2,728547 -1,421732
2		 1	1 2	7,030501 6,645079
3		1 0	1 2	0,367436 -0,0408892
4		2 0	1 2	3,242390 3,498379
5		/2 0	1 2	4,613611 6,838201
6		0,2 0	1 2	0,0882585 0,113424
7		 0	1 2	2,638983 1,277966

Продолжение табл. 2

8		1 0	1 2	1,044510 1,266805
9		/2 0	1 2	1,365239 1,724198
10		2 1	1 2	0,896550 0,869825
11		2 0	1 2	6,654597 6,607150
12		3 0	1 2	1,825961 -0,172770
13		 /2	1 2	7,608484 96,93589
14		 0	1 2	6,757274 74,49719
15		 0	1 2	2,979530 63,82428
16		1,5 0,5	1 2	0,714272 2,275876
17		 0	1 2	16,84216 233,509