
- •Математика
- •Содержание работы
- •Раскрытие неопределенности
- •Раскрыть неопределенности
- •Математика
- •Содержание работы
- •Контрольные вопросы
- •Контрольные вопросы
- •Математика
- •Содержание работы
- •Математика
- •Содержание работы
- •Контрольные вопросы
- •Математика
- •Содержание работы
- •Раскрыть неопределенности:
- •Математика
- •Содержание работы
- •Математика
- •Содержание работы
- •Контрольные вопросы
- •Математика
- •Содержание работы
- •Кривые второго порядка
- •8.Векторная функция скалярного аргумента. Векторы скорости и ускорения. Кривизна плоской кривой.
- •Математика
- •Содержание работы
- •Математика
- •Содержание работы
- •7.1. Основная учебная литература
- •Шипачев, в. С. Высшая математика: учебник для вузов [текст] / в. С. Шипачев. – м.: Высш. Школа, 2007. – 343 с.
- •Алексеев д. В. Конспекты по общему курсу математики: учеб. Пособие для студентов инженерно-технических специальностей [электронный ресурс] / д.В. Алексеев; гу КузГту. –Кемерово, 2008.
- •Сборник задач по математике для втузов под ред. А. В. Ефимова ч.1: линейная алгебра и основы математического анализа [текст] / м.: Наука, 1990, 461 с.
Математика
Самостоятельная работа
РГР № 7 (0,139 ЗЕ)
Системы линейных уравнений
Срок выполнения 9-12 неделя
Выполнил студент группы ЭА- 111
Петров А.В.
Работу принял
Кемерово 2011
Содержание работы
-
Обратная матрица.
-
Решение матричных уравнений.
-
Ранг матрицы. Теорема Кронекера-Капелли.
-
Решение систем линейных уравнений методами обратной матрицы, Крамера, Гаусса
Литература [1,7,17]
Замечание преподавателя
1. Дайте определение
обратной
матрицы
![]() и сформулируйте условия ее существования.
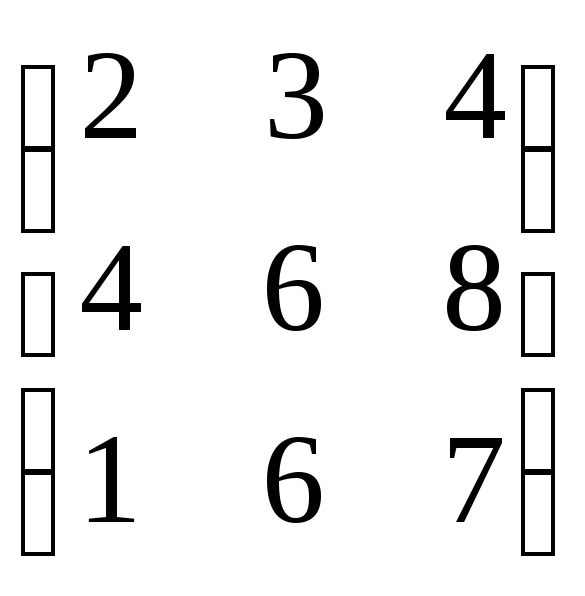
Для указанных
матриц проверьте выполнение условий
существования обратной матрицы и, если
обратная матрица существует, то найдите
ее:
и сформулируйте условия ее существования.
Для указанных
матриц проверьте выполнение условий
существования обратной матрицы и, если
обратная матрица существует, то найдите
ее:
![]() ,
,
![]() ,
,
 ,
,
 .
.
Ответы:
![]() ,
,
![]() ,
,
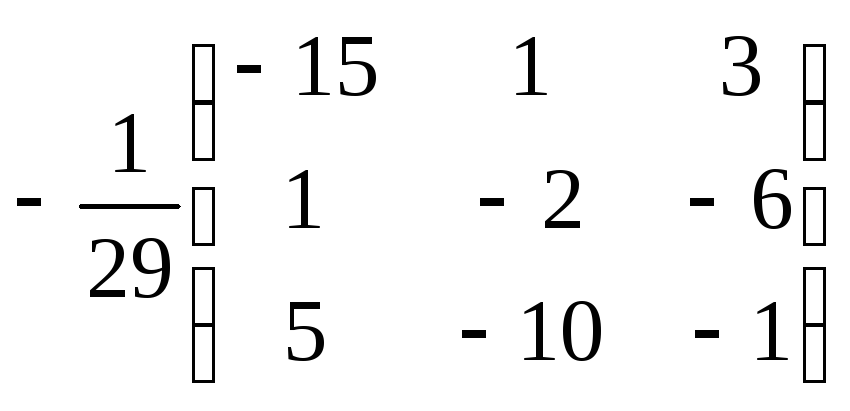
2. Выполняя действия
над матрицами, найдите неизвестную
матрицу
![]() из
указанных уравнений:
из
указанных уравнений:
![]()
![]()
a)
![]() ,
b)
,
b)
![]() ,
,
с) Найдите матрицу
![]() из
уравнения:
из
уравнения:
![]() ,
где
,
где
![]() ,
,![]() ,
,![]()
d)
![]() .
Здесь
.
Здесь
 ,
,
![]() ,
,
![]() .
.
Ответы: а)
![]() ,
b)
,
b)![]() ,
c)
,
c)
![]() ,
d)
,
d)![]()
3. Дайте определение понятия ранг матрицы. Найдите ранг матрицы методом элементарных преобразований:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
 ,
г)
,
г)
 ,
,
д)

4. Для каждой из указанных ниже систем
-
методом элементарных преобразований определите ранг матрицы системы и ранг расширенной матрицы,
-
на основании теоремы Кронекера-Капелли сделайте вывод о совместности системы (определите число решений системы),
-
найдите решения системы, при этом, если решений множество, то укажите число базисных и свободных переменных
 ,
,
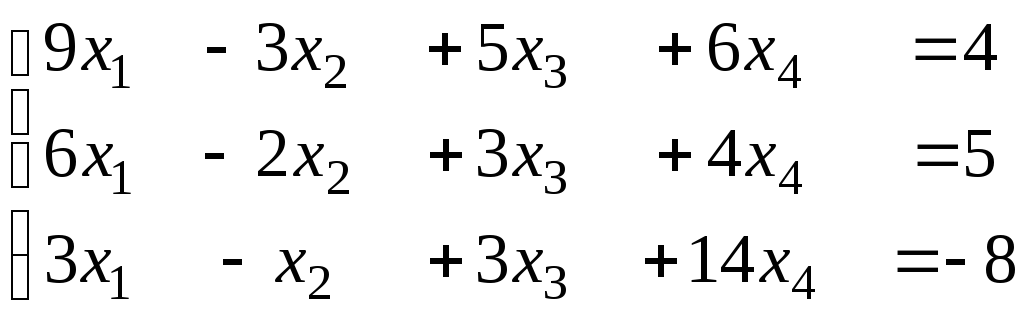
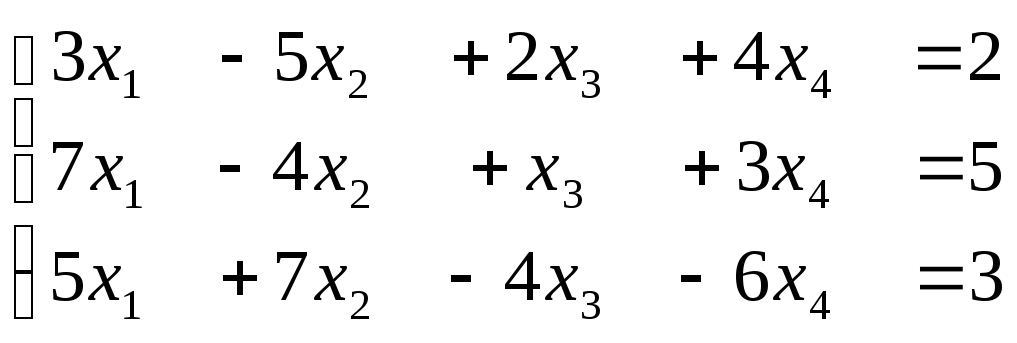 ,
,
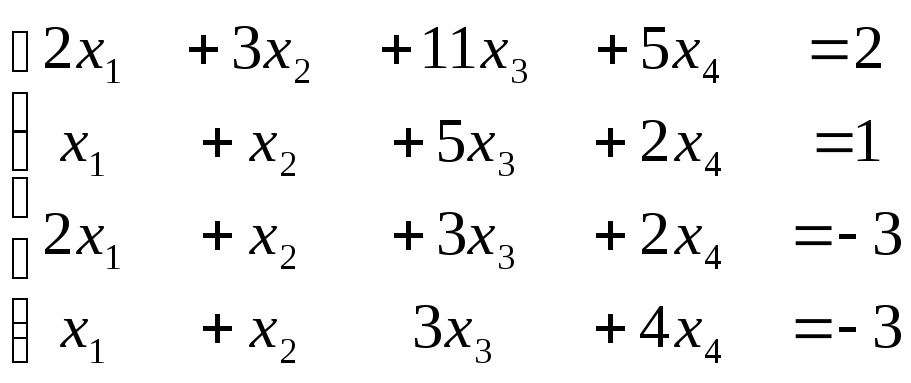
Ответы:
![]() ,
,
 ,
не имеет решений,
,
не имеет решений,
![]() .
.
Контрольные вопросы
-
Что такое порядок матрицы?
-
Матрица, стоящая слева имеет 5 столбцов и 3 строки, а матрица, стоящая справа имеет 2 столбца и 8 строк. Можно ли перемножить такие матрицы?
-
Является ли матрица
 вырожденной?
вырожденной? -
Сколько решений имеет система линейных уравнений, если ранг матрицы системы равен рангу расширенной матрицы и равен 3, а число неизвестных равно 5?
-
Справедливо ли утверждение: все уравнения системы линейно независимы и система имеет единственное решение?
Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет»
Направление подготовки 140400.62
«Электроэнергетика и электротехника»
Математика
Самостоятельная работа
РГР № 8 (0,417 ЗЕ)
Аналитическая геометрия на плоскости
Срок выполнения - 12 неделя (прямая на плоскости -0,139 ЗЕ)
- 13 неделя (0,278 ЗЕ)
Выполнил студент группы ЭА- 111
Петров А.В.
Работу принял
Кемерово 2011
