2.5 Шестнадцатеричная система счисления
Использует шестнадцать цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в их обычном смысле, а затем A=10, B=11 , C=12 , D=13 , E=14 , F=15 . Также использует символы «+» и «–» для обозначения знака числа и запятую (точку) для разделения целой и дробной частей числа. Внедрена американской корпорацией IBM. Широко используется в программировании для IBM-совместимых компьютеров. С другой стороны, в некоторых языках сохранились и следы использования этой системы счисления в прошлом. Например, в романских языках (испанском, французском и др.) числительные от 11 до 16 образуются по одному правилу, а от 17 до 19 – по другому. А в русском языке известен пуд, равный 16 килограммам.
Числа, не зависимо от системы счисления, всегда означают количество чего-нибудь. Собственно, записать число (в любой системе счисления) - это всего лишь способ записать это количество. Поэтому, можно составить таблицу соответствия между числами в разных системах счисления.
Таблица соответствия записи чисел в различных системах счисления
|
BIN |
OCT |
DEC |
HEX |
|
0 |
0 |
0 |
0 |
|
001 |
1 |
1 |
1 |
|
010 |
2 |
2 |
2 |
|
011 |
3 |
3 |
3 |
|
100 |
4 |
4 |
4 |
|
101 |
5 |
5 |
5 |
|
110 |
6 |
6 |
6 |
|
111 |
7 |
7 |
7 |
|
1 000 |
10 |
8 |
8 |
|
1 001 |
11 |
9 |
9 |
|
1 010 |
12 |
10 |
A |
|
1 011 |
13 |
11 |
B |
|
1 100 |
14 |
12 |
C |
|
1 101 |
15 |
13 |
D |
|
1 110 |
16 |
14 |
E |
|
1 111 |
17 |
15 |
F |
|
10 000 |
20 |
16 |
10 |
Существуют также нецелочисленные позиционные системы счисления. К таким относится система счисления с основанием е=2, 718281828.. – система, обладающая наибольшей плотностью записи информации
3 Перевод чисел из одной системы в другую
3.1 Перевод из десятичной сс в любую другую
При переводе чисел из десятичной системы счисления в любую другую, всегда отдельно (по разным правилам) переводится целая и дробная части.
Перевод целой части
Для того, чтобы перевести число из десятичной системы счисления в любую другую, нужно выполнять целочисленное деление исходного числа на основание той системы счисления, в которую нужно перевести число. При этом важен остаток от деления и частное. Частное нужно делить на основание до тех пор, пока не останется 0. После этого все остатки нужно выписать в обратном порядке – это и будет число в новой системе счисления.
Пример: перевод числа 25 из десятичной системы счисления в двоичную будет выглядеть следующим образом:
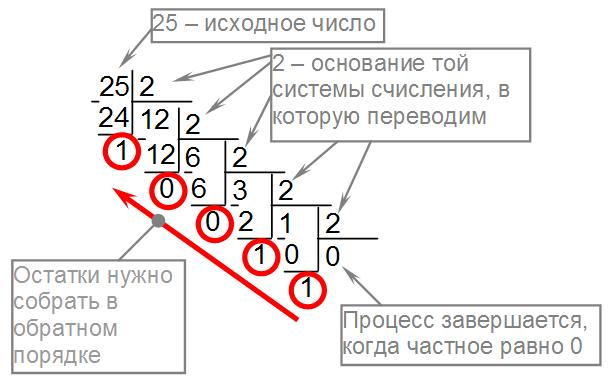
Выписав остатки в обратном порядке, получим 2510=110012.
Если задуматься, то можете легко заметить, что при переводе абсолютно любого десятичного числа в другую систему счисления самый последний остаток (то есть, самая первая цифра в результате) всегда будет равен самому последнему частному, которое оказалось меньше основания той системы счисления, в которую мы переводим число. Поэтому, деление часто останавливают раньше, чем частное станет равным нулю – в тот момент, когда частное станет просто меньше основания.
Пример: перевод 39310 в шестнадцатеричную систему счисления.
Выписав остатки в обратном порядке, получим 39310=18916.
Нужно понимать, что остатки получаются в десятичной системе счисления. При делении на 16 могут появиться остатки не только от 0 до 9, но также и остатки от 10 до 15, которые заменятся соответственно цифрам A-F. Каждый остаток - это всегда ровно одна цифра в той системе счисления, в которую осуществляется перевод.
Перевод дробной части
При переводе дробной части – в отличие от перевода целой части – нужно не делить, а умножать на основание той системы счисления, в которую мы переводим. При этом каждый раз отбрасываются целые части, а дробные части снова умножаются. Собрав целые части в том порядке, в каком они появились, получается дробная часть числа в нужной системе счисления.
Одна операция умножения даёт ровно один дополнительный знак в системе счисления, в которую осуществляется перевод.
При этом существует два условия завершения процесса:
1) в результате очередного умножения вы получили ноль в дробной части. Это означает, что число перевелось из десятичной системы счисления в нужную точно.
2) не все числа можно перевести точно. В таком случае обычно переводят с некоторой точностью. При этом сначала определяют, сколько знаков после запятой будет нужно – именно такое количество раз и нужно будет выполнить операцию умножения.
Вот пример перевода числа 0.3910 в двоичную систему счисления. Точность - 8 разрядов (в данном случае точность перевода выбрана произвольно):
Если выписать целые части в прямом порядке, то получим 0.3910=0.011000112.
Самый первый ноль (на рисунке перечёркнут синим) выписывать не нужно – так как он относится не к дробной части, а к целой.
Вот так будет выглядеть перевод числа 0.3910 в шестнадцатеричную систему счисления. Точность - 8 разрядов в данном случае точность снова выбрана произвольно:
Если выписать целые части в прямом порядке, то получим 0.3910=0.63D700A316.
При этом Вы, наверное, заметили, что целые части при умножении получаются в десятичной системе счисления. Эти целые части, полученные при переводе дробной части числа следует интерпретировать точно так же, как и остатки при переводе целой части числа. То есть, если при переводе в шестнадцатеричную систему счисления целые части получились в таком порядке: 3, 13, 7, 10, то соответствующее число будет равно 0.3D7A16.
Перевод числа с целой и дробной частью
Чтобы выполнить перевод числа с целой и дробной частью, нужно отдельно перевести целую и дробную части, а потом эти две части записать вместе.
Например, 25.3910=11001.011000112.
Перевод небольших целых чисел из десятичной СС в двоичную в уме
Поскольку при работе с различными системами счисления, особенно при разработке программ, очень часто возникает необходимость перевода небольших целых чисел, то, вообще говоря, имеет смысл запомнить таблицу соответствия для первых 16 чисел (от 0 до 15).
Но если разобраться, как легко в уме переводить небольшие целые числа от 0 до 15 из десятичной системы счисления в двоичную, то значительную часть таблицы вы сможете просто вычислять в уме каждый раз, когда это будет нужно.
Итак, чтобы перевести небольшое положительное целое число от 0 до 15 из десятичной системы счисления в двоичную, первое, что нужно понять: каждой позиции в двоичном числе соответствует степень двойки. При этом степени двойки для позиций от 0 до 3 запомнить очень просто – это числа 1, 2, 4 и 8.
Далее, десятичное число, которое вы хотите перевести в двоичную систему счисления, нужно представить в виде суммы чисел 1, 2, 4 и 8, причём каждое число можно использовать не больше одного раза. Такое представление можно сделать только одним-единственным способом.
Когда вы получили список чисел, которые должны войти в сумму, в позициях, соответствующих этим числам, нужно поставить единички, в остальных - нолики. Например, число 5 – это 4 плюс 1:
|
8 |
4 |
2 |
1 |
|
0 |
1 |
0 |
1 |
А число 10 – это 2 плюс 8:
|
8 |
4 |
2 |
1 |
|
1 |
0 |
1 |
0 |
Число 15 можно получить только сложив все числа 1, 2, 4, 8:
|
8 |
4 |
2 |
1 |
|
1 |
1 |
1 |
1 |
Аналогичным же образом – разложением по степеням двойки – можно получать и другие небольшие числа в двоичной системе.