§3 Дробово-лінійна функція. Властивості і відображення здійснювані нею

Функція виду , де і називається дробово-лінійною. Розглянемо частковий випадок цієї функції, коли . Тоді будемо мати функцію , яку природно називати лінійною. Найближчою нашою метою є встановлення характеру відображення, що здійснюються цією функцією.

Оскільки випадок нецікавий, то вважатимемо, що . При будемо мати, що , а це є паралельне перенесення комплексної площини на себе на вектор . При цьому, як ми знаємо з геометрії, зберігаються не тільки кути, а й відстані. Ясно, що нескінченно віддалена точка відображається сама в себе. Тому це відображення є конформним () відображенням розширеної комплексної площини на себе.

Нехай . Спробуємо знайти таке комплексне число , щоб відображення можна було переписати у вигляді . Таке можна знайти, в нашому випадку . Знайдемо похідну: . Таким чином похідна в кожній точці є сталою і відмінною від 0. Тоді в цьому випадку це відображення буде гомотетією з коефіцієнтом і центром в точці і поворотом відносно точки на кут, що дорівнює . Очевидно це відображення буде взаємо однозначним відображенням розширеної комплексної площини на себе і звісно конформним. Причому всі вектори в будь-якій точці будуть повертатися на один і той же кут.

Нехай тепер . Розглянемо відображення (). Це відображення кожну скінченну точку -площини, крім точки переводить в скінченну точку -площини, причому переводить однозначно. Неважко перевірити, що кожне скінченне значення , крім досягається лише при одному значенні . Ясно, що

, .

Тому можна вважати, що це відображення нескінченно віддалену точку переводить в точку (поряд з цим з - площини ніяких скінченних прообразів не має) і точку -площини переводить в - площини (і нескінченно віддалена точка ніяких інших прообразів в -площині не має). Все це дозволяє стверджувати, що дробово-лінійне відображення () взаємно однозначно відображає розширену комплексну площину на себе.

З’ясуємо чи це відображення буде конформним. Для цього достатньо перевірити чи існує , .

.

існує в довільній точці - площини крім точки . Оскільки , то існує всюди крім точки і в кожній точці . А це означає, що дробово-лінійне відображення є конформним відображенням розширеної комплексної площини на себе. В цьому твердженні слід уточнити дві речі: що робиться з кутами між кривими, які виходять з точки - площини (адже в цій точці похідної нема і значить про конформність тут поки що говорити не приходиться), а також що розуміти під кутом між двома кривими в нескінченно віддаленій точці.

Нехай і дві криві, які виходять з точки - площини (рис. 10а). Оскільки точку відображення переходить в нескінченно віддалену точку, то образом кривих і будуть деякі криві і , які виходять з нескінченно віддаленої точки (рис. 10б). Що розуміти під кутом між кривими і . Домовимось під кутом між двома кривими і в нескінченно віддаленій точці розуміти кут між образами цих кривих і в точці 0 при відображенні (рис. 10в). Тоді подивимось на відображення - площини в

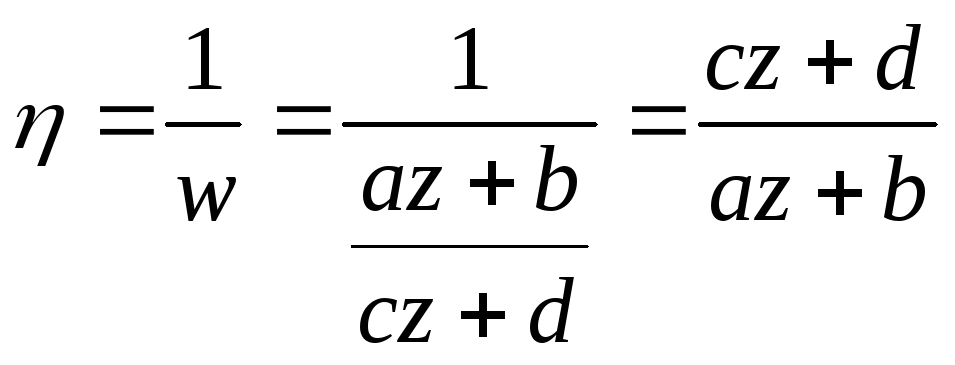- площину. Будемо мати . Оскільки це відображення є дробово-лінійним і в точці існує відмінна від 0 похідна, то воно є конформним в цій точці і значить кути між кривими і та і будуть рівними. А це все означає, згідно з нашою домовленістю, що і в точці це відображення не змінює кутів. Міркуючи аналогічно ми покажемо, що це відображення не змінюватиме кути між кривими, які виходять з нескінченно віддаленої точки -площини. Порівнявши це відображення з лінійним відображенням (див. ), можна зауважити, що на відміну від лінійного, де всі криві незалежно від точки в площині повертаються на один і той же кут , тут криві будуть повертатися на кут , який буде змінюватися із зміною точки . Проте і тут є одна особливість. Для її з’ясування дещо перетворимо нашу похідну

.

Тоді аргумент цієї похідної буде . З цього зображення видно, що якщо точки лежать на промені, який виходить з точки , то є сталою величиною для всіх точок цього променя. А це означає, що всі криві, які виходять з точок цього променя, повертають при відображенні на один і той же кут. Можна також скористатися геометричним змістом модуля похідної і побачити, що коефіцієнт розтягу тут також буде змінюватися від точки до точки, хоча і тут є множини, де цей коефіцієнт буде сталим (зокрема на одній з них він буде дорівнювати 1).

П.1 Група дробово-лінійних відображень

Позначимо через множину все можливих відображень (). Відображення будемо називати тотожним. Задамо на множині наступну операцію: візьмемо на цій множині дробово-лінійне відображення та і подивимося чи послідовне виконання цих дробово-лінійних відображень з відмінними від 0 визначниками дасть дробово-лінійне відображення -площини на -площину теж з відмінним від 0 визначником. Будемо мати,

.

Таким чином, послідовне виконання цих відображень дає дробово-лінійне відображення. Легко перевірити, що визначник цього відображення відмінний від 0. Значить належить до множини і . Така дія, як ми помітили ніколи не виводить нас з множини і завжди при довільних фіксованих і з множини приводить нас до конкретного єдиного відображення з цієї ж множини, тому ця дія є операцією на і, якщо ми покажемо, що для неї виконуються аксіоми групи, то цим і встановимо, що множина відносно цих операцій є групою.

Тотожне відображення позначатимемо . Очевидно справедливо, що і : . Неважко догадатися, що якщо , то для знаходження треба з цієї рівності знайти . Простою перевіркою переконуємось, що наша операція асоціативна, а отже, все це дозволяє стверджувати, що множина із введеною на ній операцією є групою (взагалі кажучи не комутативною).

П.2. Кругова властивість дробово-лінійних відображень

Як ми знаємо рівняння задає в площині коло або пряму (пряма, коли і хоча б один з коефіцієнтів ). Останнє рівняння через комплексні числа можна переписати в дещо іншому вигляді. Оскільки,

, , ,

то

- комплексне число, - спряжене до нього, тому

(1)

Останнє рівняння, де і дійсні числа, а - комплексне число, задає коло або пряму в -площині.

Подивимось що буде образом об’єкта, що задається рівнянням (1), при відображенні . Для цього потрібно в (1) замість поставити (бо ми шукаємо образ при відображенні ). Будемо мати,

або .

А це рівняння аналогічне до рівняння (1), тільки в - площині ,а отже, воно зображатиме в цій площині теж пряму або коло. Домовимося в майбутньому для простоти викладу колом в широкому розумінні називати власне коло або пряму (як коло, що проходить через нескінченно віддалену точку).

Ми встановили, що відображення коло в широкому розумінні переводить в коло в широкому розумінні. Неважко здогадатися, як випливає з тільки що сказаного, що відображення кожну пряму або коло, які проходять через точку 0, переводить в пряму.

Подивимося що буде, коли .

.

Відображення можна зобразити у вигляді композиції відображень. А саме: , , ,

.

Нехай ми маємо коло (1) в -площині. − лінійне відображення, тому воно це коло переведе в коло. За тільки що доведеним відображення коло в широкому розумінні знову переведе в коло в широкому розумінні. Оскільки і − лінійні відображення, то кожне з них коло в широкому розумінні переведе в коло в широкому розумінні. А отже, відображення , як послідовне виконання вказаних вище відображень, коло в широкому розумінні (1) переведе в коло в широкому розумінні в -площині.

Знову неважко здогадатися, що це відображення довільне коло або пряму, які проходять через точку переведе обов’язково в пряму, а кола або прямі, які не проходять через цю точку це відображення переведе в коло.

П.3. Нерухомі точки дробово-лінійного відображення

Якщо ми маємо відображення (), то для цього відображення нескінченно віддалена точка є нерухомою (). Якщо , то, як ми знаємо, це відображення має ще одну нерухому точку − . Таким чином, подивившись на , можна сказати, що у випадку дві нерухомі точки зливаються в одну. В цьому випадку ми цю точку називатимемо подвійною нерухомою точкою. Нехай тепер , де (), . Тут зрозуміло, що нескінченно віддалена точка нерухомою не буде. Для з’ясування має чи ні таке відображення нерухомі точки розв’яжемо рівняння

, .

Дивлячись на розв’язок рівняння, робимо висновок, що якщо величина під коренем 0, то це рівняння матиме один подвійний корінь, який буде для нашого відображення подвійною нерухомою точкою. Якщо ж величина під коренем відмінна від 0, то це рівняння має два різні корені, кожен з яких і буде нерухомою точкою нашого відображення. Таким чином ми встановили

Кожне дробово-лінійне відображення з множини завжди має дві нерухомих точки, які в окремих випадках можуть зливатися в одну.

З тільки що одержаного випливає, що якщо деяке дробово-лінійного відображення має 3 нерухомих точки, то воно є тотожним.

Скористаємось цим для того, щоб відповісти на питання: „скільки пар відповідних точок треба мати, щоб однозначно задати дробово-лінійне відображення?” Нехай маємо точки , , . Треба знайти дробово-лінійне відображення , яке ці точки перевело б в точки , , .

, , .

Розглянемо відображення . Це відображення точки , , переведе в точки , , . Тепер розглянемо відображення . Очевидно відображення − це дробово-лінійне відображення, яке точки , , переводить самі в себе. Отже, відображення має 3 нерухомі точки. Тоді воно є тотожним. Отже, , . Звідси випливає, що дробово-лінійне відображення цілком визначається трьома парами відповідних точок.

Тепер виникає питання як, маючи ці відповідні точки, задати дробово-лінійне відображення. Нехай маємо три скінченні точки , , і теж три скінченні точки , , . Постараємось знайти дробово-лінійне відображення , яке перші 3 точки перевело б в точки , , . Побудуємо відображення , яке точки , , із - площини відобразить в точки 0, , 1 -площини. З того, що і маємо,

.

Скориставшись тим, що , одержимо

.

Тому маємо,

.

Ми одержали відображення, яке точки , , із - площини відображає в точки 0, , 1 -площини. Позначимо через − відображення, яке переведе точки , , - площини в точки 0, , 1 -площини. Тоді знову одержимо,

.

Позначимо через − дробово-лінійне відображення, яке точки , , перевело б в точки , , . Розглянемо відображення . Це відображення , яке точки , , відображає в точки 0, , 1.

(1)

.

Остання формула вирішує, поставлену вище, задачу, бо відображення і відомі. Але, зручніше для запису цього відображення користуватися рівністю (1), в яку замість підставити . Будемо мати

або

. (*)

Це і є відображення, записане в неявному вигляді, яке скінченні точки , , - площини переводить в точки , , - площини.

З’ясуємо як виглядатиме наше відображення, якщо серед точок -х є нескінченно віддалена точка, наприклад . Будемо мати

.

Аналогічно і з випадками, коли серед чи є нескінченно віддалена точка. Зокрема, якщо і , то відображення матиме вигляд

.

Таким чином є таке мнемонічне правило:

якщо котрась із точок чи є нескінченно віддаленою точкою, то відповідні різниці, які містять ці точки, замінюються в одержаній вище формулі (*) на 1.

В математиці відоме складне відношення 4-х точок

.

З допомогою вище проведених викладок видно, що складне відношення 4-х точок є інваріантом при дробово-лінійному відображенні розширеної комплексної площини в себе.

Оскільки коло в широкому розумінні однозначно задається 3-ма точками і дробово-лінійне відображення теж задається 3-ма парами відповідних точок, то очевидно має місце наступний факт: якщо в - площині є коло в широкому розумінні з 3-ма заданими на ньому точками , , і в - площині також є коло в широкому розумінні з 3-ма заданими на ньому точками , , , то існує єдине дробово-лінійне відображення, яке вказане коло - площини відобразить у вказане коло - площини так, що точки , , перейдуть при цьому відповідно в точки , , .

Нехай ми в - площині маємо коло в широкому розумінні і - одна із областей, на які розширену - площину ділить крива . І нехай , , − точки на кривій (рис. 11). Тоді − це буде та область, яка залишається зліва від спостерігача, який іде по колу від точки до точки через точку . А в - площині є теж коло в широкому розумінні і три точки на ньому , , - це та із двох областей розширеної -площини, на які ділить останню, яка залишається зліва від спостерігача, який іде з точки до точки через точку (рис. 12).

Знайти дробово-лінійне відображення, яке , і . Побудуємо дробово-лінійне відображення (скориставшись попереднім пунктом), яке , , , . Це буде якесь дробово-лінійне відображення, яке крім того розширену комплексну - площину взаємно однозначно переведе на розширену -площину. Проведемо через точку дугу кола в широкому розумінні, яке ортогональне до кола і ця дуга починається в точці і закінчується в якійсь точці області . Тоді точку , яка є образом цієї точки , треба вибрати так, щоб відрізок кола в широкому розумінні (прямої) в нас був проведений таким чином, щоб поворот відбувався на цю ж величину і в цьому напрямі. Ясно, що така точка має бути області . Так видно, що довільна точка має образ, що лежить в області . Отже, відображається в . Насправді це відображення буде "на", бо якщо припустити, що в є точка , яка є образом якоїсь точки не з області , то легко прийдемо до суперечності з тим, що точу і точку не можна з'єднати дугою кола в широкому розумінні без перетину кривої .

З розв'язаної задачі випливає, що якщо потрібно відобразити якусь область -площини, яка одержується в результаті проведення кола в широкому розумінні, на якусь область -площини, яка отримується в результаті проведення в - площині кола в широкому розумінні, то потрібно на колі в широкому розумінні - площини вибрати три точки , , і подивитися з якої сторони від спостерігача знаходиться ця область, якщо рухатися з точки до точки через точку . Тоді на вказаному колі - площини точки , , слід вибирати так, що якщо ми будемо рухатися від точки до точки через точку , то щоб потрібна - область лежала з тієї ж сторони, що і в -площині.

Приклад. Відобразити верхню півплощину - площини () на зовнішність одиничного кола в - площині так, щоб точки , , перейшли в точки , , .

Використавши формулу (*), будемо мати,

.

Оскільки область знаходиться зліва від спостерігача, який іде вздовж дійсної осі від точки до точки через точку і область теж знаходиться зліва від спостерігача, який рухається по колу від точки до точки через точку (рис. 13), то одержане відображення і розв’язує нашу задачу.

Нехай в - площині маємо деяку пряму і дві точки симетричні відносно цієї прямої, то зрозуміло, що пряма, яка проходить через ці дві точки і довільне коло з центром на даній прямій, що проходить через ці точки, будуть ортогональні до даної прямої. І навпаки, якщо є деяка пряма, що проходить через дві точки, яка перпендикулярна до прямої і всяке коло, що проходить через ці точки з центром на прямій , яке перпендикулярне до , то ці точки симетричні відносно прямої .

Подивимося, що буде робитися з цими точками при дробово-лінійному відображенні і , − точки симетричні відносно неї. Нехай ми маємо дробово-лінійне відображення , яке нехай спочатку пряму переведе в пряму -площини. Тоді це відображення всяке коло, яке проходить через і з центром на , переведе в коло, яке буде ортогональним до (в результаті конформності відображення) і пряму, яка пройде через і переведе в коло, яке буде ортогональним до .Точки і перейдуть в точки і . З вище сказаного випливає, що ці точки і будуть симетричними відносно (бо ми тільки що встановили, що всяке коло, яке проходить через точки і , ортогональне до і пряма, яка пройде через ці точки, теж ортогональна до ).

Зауважимо, що якщо задана пряма в -площині, наприклад , то маючи якусь точку можна одержати точку , яка симетрична відносно цієї прямої.

Ми встановили, що при дробово-лінійному відображенні зберігається симетрія відносно прямої. А оскільки дробово-лінійне відображення пряму може перевести в коло, то можна говорити у зв'язку з цим і про симетрію відносно кола і про збереження симетричних відносно кола точок при дробово-лінійному відображенні.