
- •П.1 Логарифмічна функція і її властивості ………………………………… 48
- •Розділ 1. Вступні зауваження і факти
- •§1. Комплексні числа. Операції над комплексними числами
- •§2. Збіжність послідовностей комплексних чисел
- •§3 Нескінченно віддалена точка. Розширена комплексна площина. Стереографічна проекція
- •§4 Ряди комплексних чисел
- •§5 Комплекснозначні функції комплексного аргументу та деякі їх властивості
- •Розділ 2. Похідна функції комплексного аргументу. Аналітичні функції
- •§1 Похідна функції комплексної змінної. Критерій її існування
- •Доведення
- •§2 Геометричний зміст аргументу і модуля похідної
- •§3 Дробово-лінійна функція. Властивості і відображення здійснювані нею
- •§4 Експоненціальна і тригонометрична функції в комплексній області
- •П.1 Логарифмічна функція і її властивості
- •§5 Виділення однозначних віток многозначної функції
- •§6 Показникова та степенева функції в комплексній області
- •Розділ 3. Інтеграл в комплексній області
- •§1 Означення інтеграла від функції комплексної змінної та його властивості
- •§2 Інтегральна теорема Коші
- •Доведення
- •Доведення
- •§3 Інтегральна формула Коші та наслідки з неї
- •Доведення
- •Доведення
- •Розділ 4. Функціональні ряди в комплексній області
- •§1 Збіжність та рівномірна збіжність функціональних рядів в комплексній області. Теорема Вейєрштрасса про рівномірно збіжні ряди аналітичних функцій
- •Доведення
- •§2 Степеневі ряди в комплексній області
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§3 Ряди Лорана
- •Доведення
- •Розділ 5. Лишки та їх застосування
- •§1 Особливі точки аналітичної функції та їх класифікація
- •Доведення
- •Доведення
- •Доведення
- •Доведення
- •§2. Теорема про лишки та її застосування. Обчислення лишків
- •§3 Принцип аргументу
- •Доведення
- •§4 Поняття про цілу функцію та лишки відносно нескінченно віддаленої точки
- •Висновок
- •Список використаної літератури:
§5 Виділення однозначних віток многозначної функції
П риклад
софізму Бернуллі переконує нас в тому,
що оперування многозначними функціями
може привести до різноманітних проблем
і помилок. Таким чином, нам слід навчитись
як із многозначних функцій виділяти
однозначні вітки. Все, що ми тут зробимо
в загальному обґрунтовуватись не буде,
а те, що буде робитися для конформних
функцій буде випливати з природи
відображень, що здійснюються цими
функціями.
риклад
софізму Бернуллі переконує нас в тому,
що оперування многозначними функціями
може привести до різноманітних проблем
і помилок. Таким чином, нам слід навчитись
як із многозначних функцій виділяти
однозначні вітки. Все, що ми тут зробимо
в загальному обґрунтовуватись не буде,
а те, що буде робитися для конформних
функцій буде випливати з природи
відображень, що здійснюються цими
функціями.
Нехай
ми маємо функцію
![]() ,
яка задана в області
,
яка задана в області
![]()
![]() -площини.
Часто ця область
-площини.
Часто ця область
![]() буде співпадати зі всією розширеною
площиною. Припустимо, що область
буде співпадати зі всією розширеною
площиною. Припустимо, що область
![]() вдалося розбити на області
вдалося розбити на області
![]() ,
,
![]() ,
,
![]() ,...,
,...,
![]() так, що: 1) вони не мають спільних внутрішніх
точок, а тільки хіба що спільні межові
точки, 2) об’єднання їх дає область
так, що: 1) вони не мають спільних внутрішніх
точок, а тільки хіба що спільні межові
точки, 2) об’єднання їх дає область
![]() ,
3) відображення
,
3) відображення
![]() кожну з цих областей взаємо однозначно
відображає на відповідно області
кожну з цих областей взаємо однозначно
відображає на відповідно області
![]() ,
,
![]() ,
,
![]() ,...,
,...,
![]()
![]() -
площини (часто, зокрема в прикладах, які
ми будемо застосовувати нижче всі
-
площини (часто, зокрема в прикладах, які
ми будемо застосовувати нижче всі
![]() будуть співпадати між собою). Тоді
розглянемо обернену функцію
будуть співпадати між собою). Тоді
розглянемо обернену функцію
![]() ,
яка взагалі кажучи в
,
яка взагалі кажучи в
![]() -
площині буде многозначною. Якщо ж ми
будемо цю функцію розглядати в області
-
площині буде многозначною. Якщо ж ми
будемо цю функцію розглядати в області
![]() і вимагати, щоб її значення попадали в
область
і вимагати, щоб її значення попадали в
область
![]() ,
то так одержану функцію називають
однозначною
віткою
многозначної функції
,
то так одержану функцію називають
однозначною
віткою
многозначної функції
![]() .
Покажемо як все це працює на двох
прикладах:
.
Покажемо як все це працює на двох
прикладах:
-
Розглянемо функцію
 .
.
Ми
знаємо про цю функцію, що вона кути
розхилом
![]() з вершиною в початку координат
з вершиною в початку координат
![]() -
площини переводить в кути розхилом
-
площини переводить в кути розхилом
![]() з вершиною в початку координат
з вершиною в початку координат
![]() -
площини. А значить області
-
площини. А значить області
![]() ,
про які тільки що йшлося, будуються
так: в
,
про які тільки що йшлося, будуються
так: в
![]() -
площині проводимо промінь під кутом
-
площині проводимо промінь під кутом
![]() до дійсної осі, від цього променя будуємо
інший під кутом
до дійсної осі, від цього променя будуємо
інший під кутом
![]() до цього променя і т.д. (рис. 17). Тоді це
відображення
до цього променя і т.д. (рис. 17). Тоді це
відображення
![]() кожну із областей
кожну із областей
![]() переведе на всю – площину з розрізом
по променю, який виходить з початку
координат під кутом
переведе на всю – площину з розрізом
по променю, який виходить з початку
координат під кутом
![]() до дійсної осі. Причому це відображення
буде однолистним в кожній із областей
до дійсної осі. Причому це відображення
буде однолистним в кожній із областей
![]() .
Області
.
Області
![]() ,
про які йшлося вище, співпадають зі
всією площиною з розрізом по променю,
про який ми тільки що говорили. А це
означає, що якщо ми розглянемо функцію
,
про які йшлося вище, співпадають зі
всією площиною з розрізом по променю,
про який ми тільки що говорили. А це
означає, що якщо ми розглянемо функцію
![]() в області
в області
![]() і поставимо вимогу, щоб значення
і поставимо вимогу, щоб значення
![]() належали області
належали області
![]() ,
то ми вже тепер одержимо однозначну
функцію, яку ми назвемо однозначною
віткою многозначної функції
,
то ми вже тепер одержимо однозначну
функцію, яку ми назвемо однозначною
віткою многозначної функції
![]() .
Її ми позначатимемо
.
Її ми позначатимемо
![]() .
.
Таким чином, ми бачимо, що можна виділити
для функції
![]()
![]() однозначних віток.
однозначних віток.
Якщо ми зафіксуємо значення
![]() в якійсь однозначній вітці і будемо
робити повний обхід точкою
в якійсь однозначній вітці і будемо
робити повний обхід точкою
![]() навколо початку координат, то після
однократного обходу аргумент цього
числа збільшиться на
навколо початку координат, то після
однократного обходу аргумент цього
числа збільшиться на
![]() ,
а отже, ми із значення в цій вітці
перейдемо до відповідного значення
наступної вітки. Коли ми зробимо таких
,
а отже, ми із значення в цій вітці
перейдемо до відповідного значення
наступної вітки. Коли ми зробимо таких
![]() обходів навколо точки 0, то ми знову
повернемося до значення, з якого починали.
Точка, яка має таку властивість,
називається алгебраїчною точкою
розгалуження
обходів навколо точки 0, то ми знову
повернемося до значення, з якого починали.
Точка, яка має таку властивість,
називається алгебраїчною точкою
розгалуження
![]() -го порядку функції
-го порядку функції
![]() .
Оскільки обхід навколо точки 0 є одночасно
і обходом навколо нескінченно віддаленої
точки, то ці точки є алгебраїчні точки
розгалуження функції
.
Оскільки обхід навколо точки 0 є одночасно
і обходом навколо нескінченно віддаленої
точки, то ці точки є алгебраїчні точки
розгалуження функції
![]()
![]() -го
порядку.
-го
порядку.
Підсумовуючи
сказане вище про функцію
![]() ,
можна зауважити, що
,
можна зауважити, що
область
![]() в
в
![]() -
площині, в якій можна виділяти однозначні
вітки функції
-
площині, в якій можна виділяти однозначні
вітки функції
![]() ,
повинна бути такою, щоб ми не могли в
цій області зробити повний оберт навколо
початку координат, а це можна робити
тоді, коли область
,
повинна бути такою, щоб ми не могли в
цій області зробити повний оберт навколо
початку координат, а це можна робити
тоді, коли область
![]() буде мати межу, що з’єднує
обидві точки розгалуження: це
може бути довільний промінь, який
виходить з початку координат або якась
гладка крива, яка з’єднує
точки 0 і
буде мати межу, що з’єднує
обидві точки розгалуження: це
може бути довільний промінь, який
виходить з початку координат або якась
гладка крива, яка з’єднує
точки 0 і
![]() .
.
Всі
сказані вище ідеї можуть бути перенесені
на дещо більш загальні функції
![]() і
і
![]() .
Можна показати, що перша з них має точки
розгалуження
.
Можна показати, що перша з них має точки
розгалуження
![]() та
та
![]() і отже область, в якій можна виділяти
однозначні вітки цієї функції, буде в
і отже область, в якій можна виділяти
однозначні вітки цієї функції, буде в
![]() -
площині з розрізом по променю, який
виходить з точки
-
площині з розрізом по променю, який
виходить з точки
![]() .
Друга з цих функцій буде мати точки
розгалуження
.
Друга з цих функцій буде мати точки
розгалуження
![]() і
і
![]() і отже, область
і отже, область
![]() -
площини, де можна виділяти однозначні
вітки цієї функції, буде вся
-
площини, де можна виділяти однозначні
вітки цієї функції, буде вся
![]() -
площина з розрізом по напрямленому
відрізку, що з’єднує точки
-
площина з розрізом по напрямленому
відрізку, що з’єднує точки
![]() і
і
![]() .
.
Вище
ми працювали з окремими вітками
многозначної функції
![]() .
Але, взагалі кажучи, кожна окрема вітка
многозначної функції не дає повного
уявлення про всю многозначну функцію.
Для того, щоб таке уявлення утворилося
і для того, щоб підвести многозначну
функцію під однозначну функцію
використовують так звані поверхні
Рімана. Вони будують зокрема під кожну
многозначну функцію, як буде видно після
побудови цієї поверхні для функції
.
Але, взагалі кажучи, кожна окрема вітка
многозначної функції не дає повного
уявлення про всю многозначну функцію.
Для того, щоб таке уявлення утворилося
і для того, щоб підвести многозначну
функцію під однозначну функцію
використовують так звані поверхні
Рімана. Вони будують зокрема під кожну
многозначну функцію, як буде видно після
побудови цієї поверхні для функції
![]() .
Многозначна функція
.
Многозначна функція
![]() взаємо однозначно відображає свою
поверхню Рімана на розширену
взаємо однозначно відображає свою
поверхню Рімана на розширену
![]() -
площину.
-
площину.
Побудуємо
поверхню Рімана для функції
![]() .
Як ми знаємо ця функція є оберненою до
функції
.
Як ми знаємо ця функція є оберненою до
функції
![]() .
Області однолистності функції в
.
Області однолистності функції в
![]() -
площині побудуємо наступним чином: 1-й
промінь направимо по додатному напрямку
дійсної осі, а всі інші під кутом
-
площині побудуємо наступним чином: 1-й
промінь направимо по додатному напрямку
дійсної осі, а всі інші під кутом
![]() до попереднього (див. рис. 18а).
до попереднього (див. рис. 18а).

Візьмемо
![]() (
(![]() )
)
![]() -площин:
(
-площин:
(![]() ),
(
),
(![]() ),…,
(
),…,
(![]() ),
які для наочності вважатимемо аркушами
паперу необмежених розмірів, і всі ці
площини розріжемо по додатній частині
дійсної осі, включаючи і точку
),
які для наочності вважатимемо аркушами
паперу необмежених розмірів, і всі ці
площини розріжемо по додатній частині
дійсної осі, включаючи і точку
![]() (на рис. 19 зображено три такі площини).
Цей розріз поділить кожну півплощину
(на рис. 19 зображено три такі площини).
Цей розріз поділить кожну півплощину
![]() на дві частини: нижню (
на дві частини: нижню (![]() )
і верхню (
)
і верхню (![]() )
(
)
(![]() ).
Тепер склеїмо всі півплощини
).
Тепер склеїмо всі півплощини
![]() уздовж додатної частини дійсної осі
(включаючи і точку
уздовж додатної частини дійсної осі
(включаючи і точку
![]() )
так: нижню першої півплощини – з верхньою
частиною другої півплощини, нижню другої
півплощини – з верхньою частиною третьої
півплощини і т. д., нижню частину (
)
так: нижню першої півплощини – з верхньою
частиною другої півплощини, нижню другої
півплощини – з верхньою частиною третьої
півплощини і т. д., нижню частину (![]() )-
ї півплощини – з верхньою частиною
)-
ї півплощини – з верхньою частиною
![]() -ї
півплощини і, нарешті, нижню частину
-ї
півплощини і, нарешті, нижню частину
![]() -ї
півплощини – з верхньою частиною першої
півплощини. Зауважимо, що коли перші
-ї
півплощини – з верхньою частиною першої
півплощини. Зауважимо, що коли перші
![]() склеювань можна фактично здійснити, то
останнє ,
склеювань можна фактично здійснити, то
останнє ,
![]() -не,
склеювання фактично здійснити не можна,
оскільки між верхньою частиною першої
півплощини і нижньою частиною
-не,
склеювання фактично здійснити не можна,
оскільки між верхньою частиною першої
півплощини і нижньою частиною
![]() -ї
півплощини міститиметься
-ї
півплощини міститиметься
![]() лист. Останнє склеювання треба розуміти
лише так, що в уяві ототожнюємо точки
додатної частини дійсної осі верхньої
частини першої півплощини і відповідні
точки додатної частини дійсної осі
нижньої частини
лист. Останнє склеювання треба розуміти
лише так, що в уяві ототожнюємо точки
додатної частини дійсної осі верхньої
частини першої півплощини і відповідні
точки додатної частини дійсної осі
нижньої частини
![]() -ї
півплощини. В результаті такого склеювання
дістанемо замкнену
-ї
півплощини. В результаті такого склеювання
дістанемо замкнену
![]() -
листу поверхню, яку називають рімановою
поверхнею функції
-
листу поверхню, яку називають рімановою
поверхнею функції
![]() .
.
Рис.
19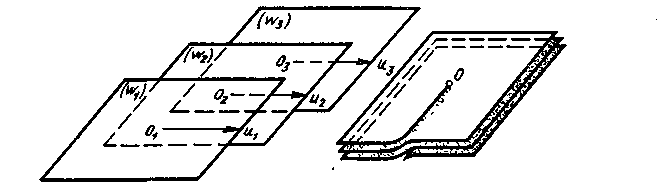
Між
точками
![]() -
площини і точками поверхні Рімана
функції
-
площини і точками поверхні Рімана
функції
![]() за допомогою рівності
за допомогою рівності
![]() здійснюється взаємно однозначна і
неперервна відповідність. Якщо точка
здійснюється взаємно однозначна і
неперервна відповідність. Якщо точка
![]() ,
переходячи з області
,
переходячи з області
![]() в область
в область
![]() ,
з
,
з
![]() в
в
![]() і т. д., опише замкнений контур навколо
початку координат, то точка
і т. д., опише замкнений контур навколо
початку координат, то точка
![]() ,
переходячи з одного листа ріманової
поверхні функції
,
переходячи з одного листа ріманової
поверхні функції
![]() на інший і побувавши, таким чином, на
всіх листах цієї ріманової поверхні,
опише також замкнений контур. Довільну
точку
на інший і побувавши, таким чином, на
всіх листах цієї ріманової поверхні,
опише також замкнений контур. Довільну
точку
![]() ріманової поверхні ми можемо сполучити
неперервною кривою з довільною іншою
точкою
ріманової поверхні ми можемо сполучити
неперервною кривою з довільною іншою
точкою
![]() цієї поверхні. Якщо ці дві точки мають
один і той же афікс, то вони на рімановій
поверхні лежать одна над одною. Якщо на
рімановій поверхні виділити яку-небудь
область
цієї поверхні. Якщо ці дві точки мають
один і той же афікс, то вони на рімановій
поверхні лежать одна над одною. Якщо на
рімановій поверхні виділити яку-небудь
область
![]() ,
що не містить частин. Які взаємно
накладаються, то для кожного
,
що не містить частин. Які взаємно
накладаються, то для кожного
![]() матимемо єдине значення
матимемо єдине значення
![]() .
Множина всіх значень
.
Множина всіх значень
![]() для
для
![]() у
у
![]() -
площині утворює деяку область
-
площині утворює деяку область
![]() .
Функція
.
Функція
![]() відображує область
відображує область
![]() на область
на область
![]() взаємно однозначно і неперервно, і,
отже, можна говорити про певну вітку
функції
взаємно однозначно і неперервно, і,
отже, можна говорити про певну вітку
функції
![]() .
.
Побудуємо
тепер ріманову поверхню функції
![]() ,
оберненої до функції
,
оберненої до функції
![]() .
Вище було з’ясовано, що функція
.
Вище було з’ясовано, що функція
![]() відображає взаємно однозначно і
неперервно кожну область
відображає взаємно однозначно і
неперервно кожну область
![]() площини (
площини (![]() ),
обмежену прямими
),
обмежену прямими
![]() і
і
![]() (
(![]() ),
на область
),
на область
![]() ,
яка складається з усіх точок
,
яка складається з усіх точок
![]() -площини,
які не належать від’ємній частині
дійсної осі (включаючи і точку
-площини,
які не належать від’ємній частині
дійсної осі (включаючи і точку
![]() ).
Візьмемо зчисленну множину екземплярів
).
Візьмемо зчисленну множину екземплярів
![]() -
площин, розмістивши їх у такому порядку:
-
площин, розмістивши їх у такому порядку:
![]() .
.
Як і
вище, ці площини вважатимемо паперовими
аркушами необмежених розмірів. Розріжемо
їх по від’ємній частині дійсної осі
(включаючи і точку
![]() ).
Тоді кожна півплощина
).
Тоді кожна півплощина
![]() буде поділеною на дві частини: нижню
(
буде поділеною на дві частини: нижню
(![]() )
і верхню (
)
і верхню (![]() ).
Склеїмо всі ці півплощини уздовж
від’ємної частини дійсної осі так:
нижню частину півплощини
).
Склеїмо всі ці півплощини уздовж
від’ємної частини дійсної осі так:
нижню частину півплощини
![]() − з верхньою частиною півплощини
− з верхньою частиною півплощини
![]() ,
верхню частину півплощини
,
верхню частину півплощини
![]() −
з нижньою частиною півплощини
−
з нижньою частиною півплощини
![]() ,
нижню частину півплощини
,
нижню частину півплощини
![]() − з верхньою частиною півплощини
− з верхньою частиною півплощини
![]() ,
верхню частину півплощини
,
верхню частину півплощини
![]() − з нижньою частиною півплощини
− з нижньою частиною півплощини
![]() і т. д. У результаті такого склеювання
дістанемо нескінченно листу поверхню,
яка називається рімановою поверхнею
функції
і т. д. У результаті такого склеювання
дістанемо нескінченно листу поверхню,
яка називається рімановою поверхнею
функції
![]() .
Між точками
.
Між точками
![]() -
площини і точками ріманової поверхні
функції
-
площини і точками ріманової поверхні
функції
![]() за допомогою рівності
за допомогою рівності
![]() здійснюється взаємно однозначна і
неперервна відповідність.
здійснюється взаємно однозначна і
неперервна відповідність.
