4.2 Бесконечно малая и бесконечно большая последовательности

Последовательность , имеющая предел, равный нулю, называется бесконечно малой последовательностью.

Таким образом, из определения предела следует, что величина есть бесконечно малая, когда .

Теорема 4.2.1. Для того, чтобы переменная имела предел, равный а, необходимо и достаточно, чтобы выполнялось равенство , где есть бесконечно малая. (Докажите ее самостоятельно.)

Последовательность называется бесконечно большой, если

(4.2.1)

При этом пишут: или и говорят, что стремится к бесконечности.

Если бесконечно большая величина , начиная с некоторого , принимает только положительные или только отрицательные значения, то пишут

или	(4.2.2)
или	(4.2.3)

Пример переменной показывает, что может иметь место соотношение (4.2.1), в то время как не имеет места ни (4.2.2), ни (4.2.3).

Отметим следующие очевидные свойства:

1) если переменная ограничена, а - бесконечная большая, то ;

2) если абсолютная величина ограничена снизу положительным числом, а - не равная нулю бесконечно малая, то .

Докажем только второе свойство. Дано, что для некоторого числа имеет место неравенство , и для всякого существует :

.

(4.2.4)

Тогда .

Зададим произвольное и подберем по нему так, чтобы , а по подберем такое , чтобы имело место свойство (4.2.4). Тогда , что и требовалось доказать.

Из этих двух утверждений следует: , ().

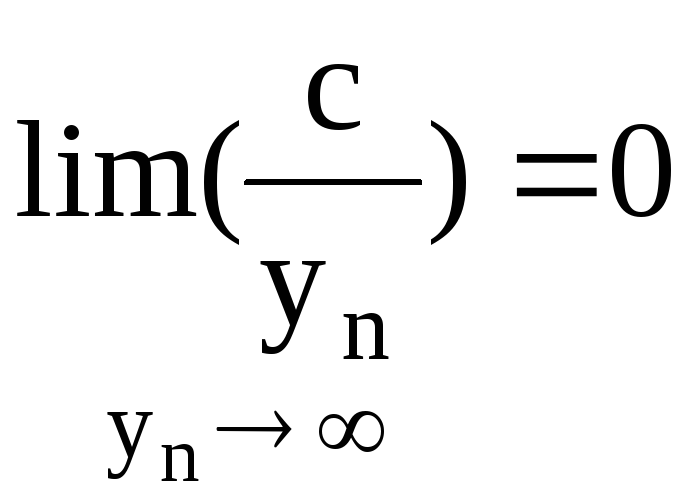Замечания:

1) если последовательность неограничена, то она не обязательно бесконечно большая. Например: не ограничена, но в ней имеются сколь угодно малые члены со сколь угодно большим нечетным номером.

Любая не равная нулю постоянная не является бесконечно малой. Из всех постоянных величин бесконечно малой является только одна – равная нулю.

Теорема 4.2.2. Произведение бесконечно малой последовательности на ограниченную является бесконечно малой последовательностью.

Запишем формулировку теоремы в символах. Если и N, то .

Доказательство:

Зададим и подберем по нему так, чтобы выполнялось неравенство . Тогда

, что и доказывает теорему.

4.3 Монотонная последовательность

Определения монотонных последовательностей уже вводились в §3. Введем их еще раз в более подробном варианте.

Определение 4.3.1. Последовательность называется возрастающей, если N .

Последовательность называется убывающей, если N .

Последовательность называется невозрастающей, если N .

Последовательность называется неубывающей, если N .

Все эти последовательности называются монотонными, а две первые – строго монотонными.

Теорема 4.3.1. Если последовательность действительных чисел не убывает и ограничена сверху числом , то существует действительное число a, не превышающее M, к которому эта последовательность стремится как к своему пределу: . Для невозрастающей и ограниченной снизу числом M последовательности действительных чисел существует действительное число a, такое, что .

Доказательство этой теоремы требует привлечения лемм, связанных со свойствами действительных чисел. Не будем приводить этого доказательства здесь, отсылая читателя к учебнику «Дифференциальное и интегральное исчисление» Я. С. Бугрова и С. М. Никольского.