11 Лекция №11. Функции, непрерывные на отрезке
11.1 Свойства функций, непрерывных на отрезке
Определение
11.1.1. Функция
называется непрерывной на отрезке
,
если эта функция непрерывна в каждой
внутренней точке этого отрезка, непрерывна
справа в точке а и непрерывна слева в
точке b.
Уточним, что значит «непрерывна справа в точке а».
Это означает, что
правый предел функции в точке а равен
значению функции в этой точке.
.
Аналогично, функция
непрерывна слева в точке b,
если
.
Рассмотрим некоторые свойства таких функций.
Теорема 11.1.1.
Если функция
непрерывна на отрезке
,
то она ограничена на нем, т.е. существует
постоянная
,
такая, что
выполняется неравенство
(рисунок 58).
Рисунок 58
Заметим, что если
функция непрерывна на интервале или
полуинтервале, то она обязательно
ограничена на нем. Например, функция
непрерывна на полуинтервале
,
но не ограничена на нем.
Доказательство:
Допустим, что
не ограничена на отрезке
.
Тогда для каждого натурального числа
n
найдется точка
,
такая, что
.
(11.1.1)
Поскольку a
и b
– конечные числа, то последовательность
ограничена, т.к. целиком находится в
отрезке. Из нее, по теореме
Больцано-Вейерштрасса, можно выделить
подпоследовательность
,
сходящуюся к некоторому пределу, равному
числу α.
,
так как
(теорема о двойном неравенстве).
Но в точке α функция
непрерывна (при α = а непрерывна справа,
при α = b
непрерывна слева).
Поэтому
.
(11.1.2)
Свойства (11.1.1) и
(11.1.2) противоречат друг другу. Значит,
функция
может быть только ограниченной на
отрезке
.
Теорема 11.1.2.
(Вейерштрасса). Если функция
непрерывна на отрезке
,
то она достигает на этом отрезке своих
минимума и максимума, то есть существуют
такие точки α и β,
и
,
что
для всех
.
Иначе говоря,
.
(См. рисунок 52).
Заметим, что если
функция разрывна на отрезке
,
то она может и не иметь наибольшего и
наименьшего значения, или и того и
другого вместе (см. рисунок 59; в точках
и
функция имеет устранимый разрыв).
Рисунок 59
Если функция непрерывна не на отрезке, а на интервале, то она также может не иметь наибольшего и наименьшего значения, как показано на рисунке 60.
Рисунок 60
Теорема 11.1.3.
Если функция
непрерывна на отрезке
и принимает на его концах значения
разных знаков (например,
,
),
то среди внутренних точек отрезка
имеется по крайней мере одна точка с,
такая, что
(как показано на рисунке 61, где таких
точек три).
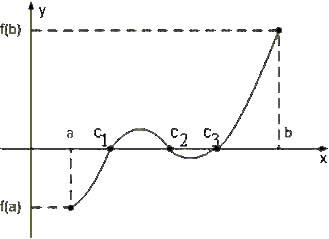
Рисунок 61
Доказательство:
Обозначим отрезок
через
.
Разделим
на две равные части. Если в середине
функция равна нулю, то теорема доказана.
Если в середине этого отрезка функция
не равна нулю, то одна из половинок
такова, что на ее концах функция принимает
значения разных знаков.
Обозначим эту
половинку через
и разделим ее на две равные части. Если
в середине
функция равна нулю, то теорема доказана.
Если нет, то обозначим через
ту половинку
,
на концах которой функция принимает
значения разных знаков.
Продолжая рассуждать
по индукции, мы либо на очередном этапе
этих рассуждений встретим точку
,
в которой
,
и тогда теорема доказана, либо получим
бесконечную последовательность вложенных
друг друга отрезков
,
на концах каждого из которых функция
имеет значения разных знаков. Тогда
существует единственная точка с,
принадлежащая всем отрезкам
,
следовательно, и отрезку
.
Очевидно, что
,
потому что, если допустить, что например,
,
то нашлась бы окрестность U(c)
точки с, такая, что
;
но этого не может быть, потому что при
достаточно большом n
отрезок
,
а функция не сохраняет знак на
.
Теорема доказана.
Два следствия из теорем о функциях, непрерывных на отрезке.
Следствие 1. Если
функция
непрерывна на отрезке
,
и
,
,
,
а С – произвольное число, находящееся
между числами А и В, то на интервале
найдется по крайней мере одна точка с,
для которой
.
Это утверждение можно сформулировать и так:
Непрерывная на
отрезке
функция принимает все промежуточные
значения между ее значениями на концах
отрезка
.
Геометрический смысл (см. рисунок 62).
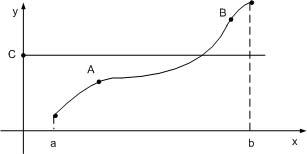
Рисунок 62
График функции
,
непрерывной на отрезке
,
имея точку А под прямой
и точку В над этой прямой, непременно
пересечет прямую
хотя бы в одной точке.
Доказательство:
Введем новую
функцию
,
где С – константа, число, находящееся
между А и В. Так как
- функция непрерывная на отрезке
,
функция F(x)
будет также непрерывна на отрезке
.
При этом очевидно,
что F(x)
принимает на концах отрезка
значения разных знаков. Тогда по теореме
11.1.3 на интервале (a,
b)
существует хотя бы одна точка с, в которой
,
или
,
т.е.
,
что и требовалось доказать.
Следствие 2.
Непрерывная на отрезке
функция принимает все промежуточные
значения между ее наименьшим и наибольшим
значениями, которые существуют по
теореме 11.1.2.
Доказательство:
Достаточно применить
следствие 1 к отрезку
,
где α, β – точки, в которых функция f(x)
достигает своих наименьшего и наибольшего
значений.
Пример 11.1.1.
Уравнение
имеет корень на интервале
.
В самом деле,
функция
непрерывна на отрезке
и на концах его принимает значения
разных знаков:
,
.