7.3 Теоремы об арифметических свойствах пределов функций.
Эти теоремы уже доказаны нами для пределов последовательностей. Докажем их для пределов функций другим способом, используя свойство конечного предела (теорему 1 предыдущего параграфа) и свойства бесконечно малых.
Теорема 7.3.1. Предел алгебраической сумы определенного числа функций, имеющих пределы, равен сумме этих пределов.
(а может быть равно
).
Доказательство:
Проведем его для двух слагаемых, так как для любого конечного числа слагаемых оно проводится так же.
Пусть
.
Тогда по теореме 7.2.1:
Значит,
но
по теореме 7.2.3.
Следовательно,
где
и по теореме 7.2.1 отсюда следует, что
Теорема 7.3.2. Предел произведения определенного числа функций, имеющих конечные пределы, равен произведению этих пределов.
Доказательство:
Проведем его для двух сомножителей.
Пусть
.
Тогда
по следствию 2 из
теоремы 7.2.4.
по следствию 1 из той же теоремы. А сумма
этих трех бесконечно малых равна
бесконечно малой по теореме 7.2.3.
Итак,
где
,
значит, по теореме 7.2.1
Следствие. Постоянный множитель можно выносить за знак предела.
Действительно,
если
.
Теорема 7.3.3.
Предел частного от деления двух функций,
имеющих пределы, равен частному этих
пределов, если предел знаменателя
отличен от нуля: если
то
Доказательство:
где
где
- число, равное
отношению пределов данных функций.
- бесконечно малая
при
,
так как числитель этой дроби – бесконечно
малая величина, а
,
следовательно,
где
а это значит, что
Теорема 7.3.4.
(о пределе степени с целым показателем).
Пусть
;
k
Z.
Тогда
Доказательство:
Поскольку
- произведение k
сомножителей, то применив для этого
произведения теорему 7.3.2, получим:
7.4 Практическое занятие №7. Предел функции. Вычисление пределов
Упражнение 7.1.
Доказать по определению, что
.
1)
а) Выберем
.
б) Выясним, для
каких значений аргумента
выполняется неравенство
.
в) Значит, неравенство
выполняется для всякого
,
если
.
г) Вывод:
.
2)
Доказательство:
Возьмем произвольное
.
Требуется найти число
> 0 такое, что
,
,
выполнялось бы неравенство
.
Учитывая, что для любых a
и b
справедливы соотношения
,
имеем
;
.
Обозначим
.
Из уравнения
,
или
находим
.
Полагая
.
Покажем, что
полученное
- искомое. Действительно, если
,
то
.
Следовательно, найдено число
такое, что
:
,
и
выполняется неравенство
.
Итак, доказали,
что
Упражнение 7.2.
Доказать,
что
(nN).
Доказательство:
Для доказательства
следует для произвольно заданного числа
найти число
такое, что
:
,
выполнялось бы неравенство
.
Из этого неравенства находим
.
Если положить
,
то
:
,
выполняется
неравенство
,
или,
.
Упражнение 7.3.
Доказать,
исходя из определения предела, что
.
Доказательство:
Пусть
- любое положительное число. Требуется
доказать, что можно подобрать такое
,
что для всех х, удовлетворяющих неравенству
,
будет выполняться неравенство
.
Если
,
то
и
.
Следовательно, для выполнения неравенства
достаточно найти k
из условия
,
т.е.
.
Итак, для любого
найдено такое k,
что из неравенства
следует неравенство
,
т.е. доказано, что
.
Предел функции не зависит от того, определена она в предельной точке или нет. Но в практике вычисления пределов элементарных функций это обстоятельство имеет существенное значение.
Если функция
является элементарной, и если предельное
значение аргумента принадлежит ее
области определения, то вычисление
предела функции сводится к простой
подстановке предельного значения
аргумента, ибо предел элементарной
функции
при х, стремящемся к значению а, которое
входит в область определения, равен
значению функции при х = а, т.е.
.
Упражнение 7.4. Найти пределы:
1)
;
Ответ:
.
Если аргумент стремится к бесконечности или к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.
Путем таких исследований, основанных на свойствах пределов, получены следующие часто встречающиеся пределы:
(постоянная
)
1.
. 2.
.
3.
. 4.
.
5.
. 6.
.
7.
8.
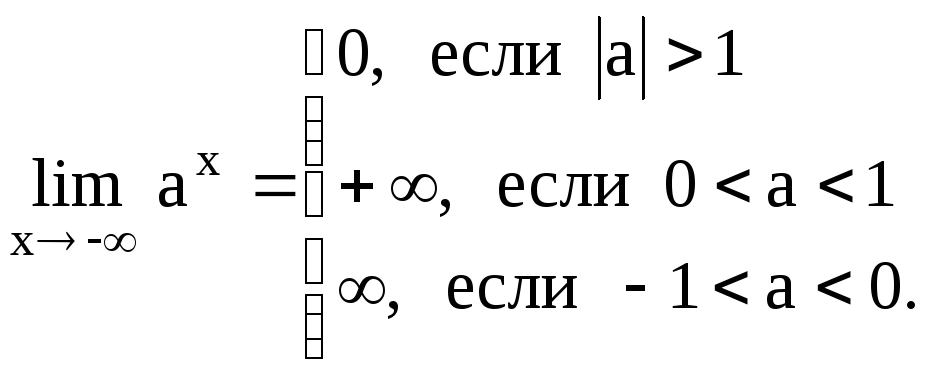
9.
10.
11.
(х есть радианная мера угла).
12.
.
Этими простейшими пределами можно пользоваться как формулами.
Более сложные
случаи нахождения предела функции,
связанные с неопределенностями видов:
рассматриваются далее каждый в
отдельности.
2)
.
Ответ:
.
3)
.
Ответ:
.
В примерах 2) и 3)
произведено домножение до разности
квадратов и суммы кубов, сделано это
для того, чтобы раскрыть неопределенность
.
Случай, когда при
или
функция f(x)
представляет отношение двух бесконечно
малых величин (случай
).
Этот случай нахождения предела функции имеет особенно важное значение. Как будет выяснено впоследствии, нахождение предела отношения бесконечно малого изменения функции к бесконечно малому изменению аргумента является одним из основных средств для изучения функций.
4)
(разлагаем
знаменатель и числитель на множители
и сокращаем дробь на
)
.
Ответ:
.
5)
(сократим дробь,
разделив на
числитель и знаменатель в отдельности)
.
Вообще, если ищется
предел дроби, числитель и знаменатель
которой многочлены, обращающиеся в нуль
в точке
,
то согласно теореме Безу1
оба многочлена разделятся без остатка
на
,
т.е. такую дробь всегда можно сократить
на
,
и каким образом избавится от
неопределенности.
Ответ:
.
6)
(разложим числитель
и знаменатель на множители и сократим
дробь на
)
.
Ответ:
.
7)
(домножим числитель
до разности квадратов, а затем сократим
дробь на (
))
.
Ответ:
.
8)
(домножим числитель
и знаменатель на произведение
,
затем сократим дробь на 1 - х)
.
Иначе можно решить
эту задачу путем замены переменной.
Полагая, что
,
получаем
,
когда
и
.
Ответ:
.
Задачи для самостоятельного решения
1. Доказать по
определению, что
.
1)
; 2)
;
3)
.
2. Вычислить пределы:
1)
; 2)
;
3)
; 4)
;
5)
; 6)
.