
- •Волновая и квантовая оптика
- •Интерференция.
- •Дифракция.
- •Поляризация.
- •Тепловое излучение.
- •Квантовая природа света.
- •Релятивистская механика.
- •Примеры решения задач.
- •Элементы атомной физики и квантовой механики.
- •Боровская теория атома водорода.
- •Волновые свойства частиц.
- •Квантовые числа. Заполнение электронных оболочек атомов.
- •Ядерные реакции .
- •Радиоактивность.
- •Примеры решения задач.
-
Элементы атомной физики и квантовой механики.
-
Боровская теория атома водорода.
-
1. Момент импульса электрона (постулат Бора)
mnrn
= n ,
,
где
m – масса электрона; n
– скорость электрона на n-ой орбите;
rn – радиус n-ой стационарной
орбиты;
 – постоянная
Планка (
– постоянная
Планка ( = h/2);
n – главное квантовое число (номер
орбиты) (n = 1,2,3...).
= h/2);
n – главное квантовое число (номер
орбиты) (n = 1,2,3...).
2. Радиус n-ой стационарной орбиты
rn = r1 n2,
где r1 – первый боровский радиус.
3. Уравнение движения электрона в атоме водорода (или водородоподобном ионе)
 (man. = Fэ),
(man. = Fэ),
где m – масса электрона, n – скорость электрона на n-ой орбите, rn – радиус n-ой орбиты, е – заряд электрона, Z – порядковый номер водородоподобного иона (для атома водорода Z = 1).
4. Энергия электрона в атоме водорода (водородоподобном ионе)
Еn = Un + Тn ,
где
 – потенциальная энергия взаимодействия
электрона с ядром,
– потенциальная энергия взаимодействия
электрона с ядром,
 – кинетическая энергия электрона, или
– кинетическая энергия электрона, или

Еn = Ei / n2,
где Еi – энергия ионизации атома водорода.
5. Энергия, излучаемая или поглощаемая атомом водорода
 ,
или
,
или
 ,
,
где n1 и n2 – квантовые числа, соответствующие энергетическим уровням, между которыми совершался переход электрона в атоме, En1 и En2 – энергия электрона на соответствующих орбитах.
6. Сериальная формула для водородоподобных ионов

 ,
,
где n1 определяет серию, n2 – отдельную линию этой серии, R – постоянная Ридберга, равна 1.097107м-1, Z – порядковый номер элемента в таблице Менделеева (для атома водорода Z = 1).
-
Волновые свойства частиц.
7. Длина волны де Бройля для частицы
 ,
,
где h – постоянная Планка, p – импульс частицы.
8. Связь импульса частицы с кинетической энергией:
а)
p = m0, p =
 (нерелятивистский случай , <<c,
Т<<E);
(нерелятивистский случай , <<c,
Т<<E);
б)
 (релятивистский случай, c,
Т Е0
или Т > Е0), где m0 – масса
покоя частицы, m – релятивистская масса,
– скорость
частицы, с – скорость света в вакууме,
Е0 – энергия покоя частицы (Е0
= mc2).
(релятивистский случай, c,
Т Е0
или Т > Е0), где m0 – масса
покоя частицы, m – релятивистская масса,
– скорость
частицы, с – скорость света в вакууме,
Е0 – энергия покоя частицы (Е0
= mc2).
9. Соотношение неопределенностей:

где х – неопределенность координаты, px – неопределенность проекции импульса на ось x, E – неопределенность энергии, t – время жизни квантовой системы в данном энергетическом состоянии.
10. Одномерное уравнение Шредингера для стационарных состояний:
 ,
,
где (х) – волновая функция, описывающая состояние частицы; Е – полная энергия, U = U(x) – потенциальная энергия частицы.
11. Вероятность обнаружения частицы в интервале от x1 до x2

где
 – плотность вероятности.
– плотность вероятности.
12. Собственная волновая функция частицы, находящейся в бесконечно глубоком одномерном прямоугольном потенциальном ящике:

где l – ширина ящика, x – координата (0 < x > 1).
13. Собственные значения энергии частицы, находящейся в одномерном потенциальном ящике:

где n – квантовое число (n=1, 2, 3...), l – ширина ящика, m – масса частицы.
-
Квантовые числа. Заполнение электронных оболочек атомов.
14. Состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:
– главным n (n=1,2,3...),
– азимутальным (орбитальным) l (l = 0,1,2,3...n-1),
– магнитным ml (ml=0, 1,
1, 2...
2... l),
l),
– спиновым ms (ms= +1/2, –1/2).
15. Обозначение оболочек и подоболочек:
Значение n 1 2 3 4 ...
Обозначение оболочки K L M N ...
Значение l 0 1 2 3 ...
Обозначение подоболочки s p d f ...
16. Модуль момента импульса электрона может принимать дискретные значения, определяемые формулой:
 ,
,
где l – азимутальное квантовое число.
17. Модуль проекции момента импульса электрона может принимать значения, определяемые формулой:
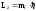 ,
,
где ml – магнитное квантовое число.
18. Число возможных состояний, соответствующих данному n:
 .
.
19. Возможны следующие состояния электрона:
n=1 : 1s.
n=2 : 2s, 2p.
n=3 : 3s, 3p,3d.
n=4 : 4s, 4p, 4d, 4f и т.д.
(см. И. В. Савельев. Курс общей физики, том 3, М. 1987г, стр.129, таб. 36.1.).
