5. Алгоритм частичного сдвига линий уровня для критерия идеальной точки (иТγ(эт)-критерий)

Процедуры, вполне аналогичные процедурам γ(УТ)-модификации, можно формализовать и применительно к ИТ-критерию. При этом, однако, надо учитывать, что в формате ИТ-критерия нет смысла обсуждать частичный сдвиг его линий уровня именно по направлению к утопической точке поля полезностей. Действительно, линии уровня этого критерия уже по определению «нацелены» на соответствующую утопическую точку поля полезностей (см. рис. 4.6 в главе 4). При этом любой их сдвиг будет рассматриваться именно как сдвиг от утопической точки поля полезностей. Тем не менее, реализовать сдвиг линий уровня ИТ-критерия в пространстве доходов, конечно же, можно (в том числе и частичный сдвиг). Требуется лишь уточнить, в каком направлении (т.е. в направлении какой из точек соответствующего пространства доходов) он будет реализован.

В контексте рассматриваемой здесь модификации введем указанную точку следующим образом. А именно, определим сначала понятие «эталонной точки» (ЭТ) в пространстве доходов. По определению, это – точка, все координаты которой равны показателю максимально возможного дохода, причем в самом благоприятном случае. Другими словами, координаты этой точки в пространстве доходов равны наибольшему элементу матрицы полезностей:

ЭТ = (; ; … ; ),

где

• = = ;

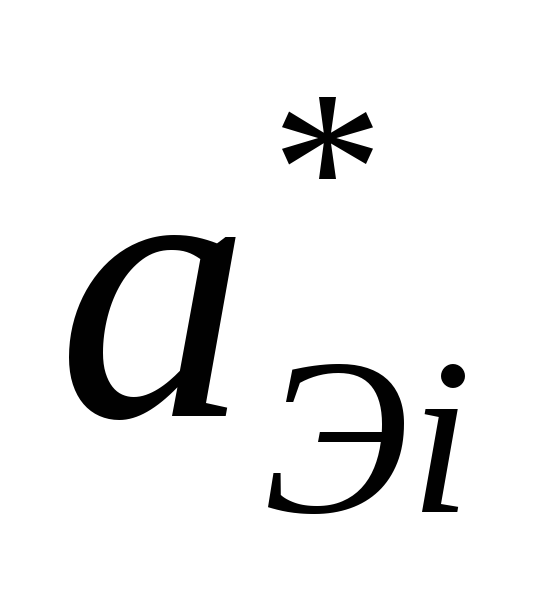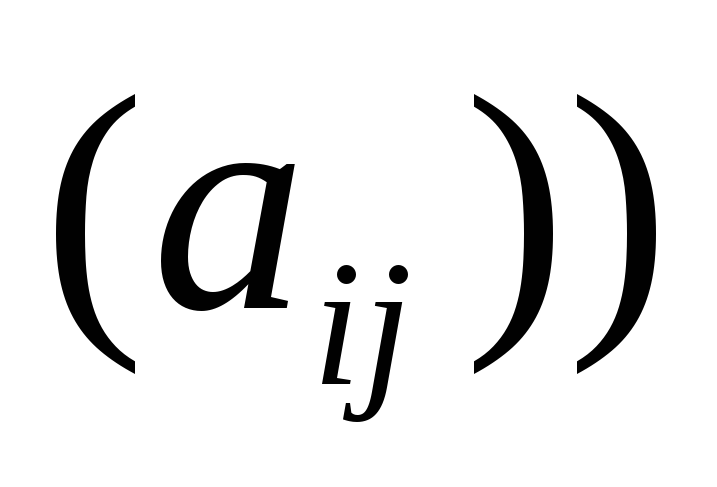• - элементы матрицы полезностей.

Любой менеджер и ЛПР в случае необходимости формализовать ситуацию, которую потребовалось бы рассматривать именно как «эталонную» (причем вариант утопической точки сразу исключается), не отказались бы от использования для этой цели именно указанной точки (ЭТ). Поэтому далее соответствующую модификацию ИТ-критерия формализуем как частичный сдвиг линий уровня указанного критерия именно к ЭТ. Получаемый в результате такой модификации новый критерий принятия решений условиях неопределенности далее обозначаем через ИТ_γ(ЭТ)-критерий.

Определим показатели/параметры соответствующих сдвигов по каждой координатной оси применительно к случаю 100% -го формата (γ=1) реализации интересующей нас модификации:

………………

(напомним, что здесь - координаты УТ).

Несмотря на новые обозначения (они обусловлены атрибутами рассматриваемого критерия), соответствующие сдвиги по осям координат в пространстве доходов полностью характеризуются компонентами вектора , который был введен ранее в начале главы. Поэтому и вектор , который в координатной форме мы записывали как

= (,, … , ),

в формате рассматриваемого здесь модифицированного критерия может быть использован для формализации понятия «частичного сдвига» (ситуация, когда 0 < γ < 1) семейства линий уровня ИТ-критерия. Еще раз подчеркнем, что это будет сдвиг уже по направлению к «эталонной» точке (ЭТ) в соответствующем пространстве доходов. Для этого перейдем от исходного представления семейства линий уровня интересующего нас критерия в исходном виде к его представлению в виде, вполне аналогичном представлению (***), но с учетом специфики направления интересующих нас сдвигов для линий уровня ИТ-критерия:

.

В интересующем нас случае параметры сдвигов по осям координат определяются, как и ранее, в формате рассмотренных выше модификаций, соответственно по формулам:

=

=

………………

= .

Другими словами, вместо семейства линий уровня «К», которые в формате ИТ-критерия задавались соотношениями

,

переходим к модифицированному представлению в виде

,

где

,

,

…. …. ….

.

Результат такого преобразования мы, как раз, и будем называть «частичным сдвигом» линий уровня ИТ-критерия по направлению к ЭТ. Подчеркнем, что указанное преобразование соответствует сдвигу анализируемых линий уровня по каждой координатной оси, причем настолько, чтобы их центр (центр соответствующих концентрических окружностей в поле полезностей) оказался именно в точке ЭТ(γ), которую формате модифицированного критерия далее будем называть опорной. Ее координаты:

ЭТ(γ) = ( … ; ).

Графическую интерпретацию (при желании) в двумерном пространстве доходов сделайте самостоятельно. При этом обратите внимание на то, что для реализации процедур выбора менеджеру достаточно пользоваться представленным ниже алгоритмом оптимизации.

Алгоритм реализации указанного критерия в задачах оптимизации решения в условиях неопределенности удобнее формализовать применительно к матрице потерь (Сэвиджа). Но при этом понадобится ее модификация, обусловливаемая требованиями учета указанного выше сдвига линий уровня ИТ-критерия. Действительно, показатель ИТ_γ(ЭТ)-критерия показывает расстояние от точки, которая характеризует в пространстве доходов альтернативу Х_i, до заданной ЛПР (при выборе γ) опорной точки ЭТ(γ). Напомним, что элементы матрицы потерь Сэвиджа, в свою очередь, показывают расстояния (по каждой координатной оси в пространстве доходов) от Х_i до точки УТ. Воспользуемся этим. Тогда алгоритм реализации ИТ_γ(ЭТ)-критерия можно представить следующими шагами.

На начальном шаге, естественно, формализуется матрица потерь Сэвиджа с элементами l_ij (см. гл. 1):

	Θ1	Θ2	…	Θn
Х1	l11	l12	…	l1n
Х2	l21	l22	…	l2n
…	…	…	…	…
Хm	lm1	lm2	…	lmn

Кроме того, на начальном шаге также уточняется конкретное значение коэффициента γ (), выбор которого должен быть реализован ЛПР в соответствии со своей системой предпочтений в пространстве доходов.

Шаг 1. Применительно к исходной матрице потерь (l_ij), которую формализовали для соответствующей задачи оптимизации решения в условиях неопределенности, с учетом формул (*) и (**) реализуются процедуры требуемого преобразования ее в формате γ(ЭТ)-модификации. В результате получается новая модифицированная матрица полезностей:

	Θ1	Θ2	…	Θn
Х1	l11+	l12+	…	l1n+
Х2	l21+	l22+	…	l2n+
…	…	…	…	…
Хm	lm1+	lm2+	…	lmn+

Шаг 2. Для указанной новой модифицированной матрицы потерь реализуются процедуры ИТ-критерия. Рассматривая элементы указанной матрицы как возможные потери относительно опорной точки ЭТ(γ) в пространстве доходов, далее стандартными (в контексте правил высшей математики и линейной алгебры) методами находим показатели ИТ_γ(ЭТ)-критерия для каждой анализируемой альтернативы. Это – расстояния в соответствующем n-мерном пространстве доходов от конкретной точки, представляющей альтернативу Х_i до указанной опорной точки ЭТ(γ):

(это – корень квадратный из суммы квадратов всех элементов по строке модифицированной матрицы потерь). Указанные показатели выписываются в дополнительном столбце, который дописывается к такой матрице.

Шаг 3. По элементам дополнительного столбца модифицированной матрицы полезностей определяется наилучшее / оптимальное решение. А именно, это – решение, которому соответствует наилучший (наименьший, т.к. анализируются потери в виде расстояния до опорной точки) показатель в дополнительном столбце указанной матрицы.

Иллюстрацию численных процедур этого метода рассмотрим (для удобства сравнения результатов) на том же примере, который уже был использован ранее.

ПРИМЕР 6.4. Для удобства изложения напомним исходные данные в рамках рассматриваемого примера. А именно, после формализации задачи принятия решений выделено множество из 4-х случайных событий, которые необходимо учитывать в рамках соответствующих решений. Кроме того, пусть анализируются 6 альтернативных решений , из которых требуется выбрать наилучшее. Соответствующая матрица полезностей имеет вид:

Решения	Доходы при событиях:
X1	5	4	3	3
X2	6	2	6	4
X3	-3	6	2	12
X4	3	9	1	5
X5	7	1	5	3
X6	6	6	1	4

Найдем наилучшее решение по ИТ_γ(ЭТ)-критерию применительно к ситуации, когда, например, ЛПР для параметра γ (в рамках указанной модификации ИТ-критерия) выбирает значение γ= 0,5.

Начальный шаг. Поскольку выбор параметра γ уже реализован (γ = 0,5), то формализуем здесь требуемую в формате процедур этого критерия матрицу потерь Сэвиджа. Сначала отметим, что соответствующая утопическая точка в поле полезностей применительно к этой задаче оптимизации имеет координаты:

Х_У = (7; 9; 6; 12).

Соответственно матрица потерь Сэвиджа имеет вид

Решения	Потери при событиях:
X1	2	5	3	9
X2	1	7	0	8
X3	10	3	4	0
X4	4	0	5	7
X5	0	8	1	9
X6	1	3	5	8

Шаг 1. Максимальная координата утопической точки составляет 12. Поэтому интересующую нас «эталонную» точку в пространстве доходов для рассматриваемого примера представляет вектор

ЭТ = (12; 12; 12; 12).

По формулам (*) определяем показатели для величин «сдвигов» по j-ой координатной оси в пространстве доходов (сначала для случая 100%-го формата реализации таких сдвигов для линий уровня ИТ-критерия):

= 12 – 7 = 5; = 12 – 9 = 3;

= 12 – 6 = 6; = 12 – 12 = 0.

После этого по формулам (**) определяем показатели с учетом требований ЛПР применительно к частичной реализации соответствующего сдвига (для γ = 0,5 это - 50% вместо 100% при указанных значениях ):

= 0,5∙5 = 2,5; = 0,5∙3 = 1,5;

= 0,5∙6 = 3; = 0,5∙0 = 0.

Соответственно с учетом формул, которые определяют координаты опорной точки ЭТ(γ), при γ=0,5 имеем

ЭТ(γ) = (9,5; 10.5; 9; 12).

Наконец, с учетом формул перехода к новым элементам матрицы потерь в формате рассматриваемого критерия выписываем модифицированную такую матрицу:

Решения	Потери при событиях:
X1	4,5	6,5	6	9
X2	3,5	8,5	3	8
X3	12,5	4,5	7	0
X4	6,5	1,5	8	7
X5	2,5	9,5	4	9
X6	3,5	4,5	8	8

Шаг 2. Припишем дополнительный столбец к полученной модифицированной матрице потерь. Его элементы находим по указанным выше формулам

Решения	Потери при событиях:				Показатель ИТγ(ЭТ)-критерия
X1	4,5	6,5	6	9	= 13, 398
X2	3,5	8,5	3	8	12,550
X3	12,5	4,5	7	0	15, 017
X4	6,5	1,5	8	7	12,550
X5	2,5	9,5	4	9	= 13,910
X6	3,5	4,5	8	8	= 12,669

Шаг 3. Определяем самый маленький элемент в дополнительном столбце модифицированной матрицы потерь. Он равен 12,550 (и выделен в дополнительном столбце матрицы). Соответствующие альтернативные решения (альтернативы X₂ и X₄) являются оптимальными по ИТ _γ(ЭТ)-критерию (при γ = 0,5). Любая из них может быть выбрана в качестве наилучшей. Кстати, объясните самостоятельно, почему (с учетом контекста понятия доминирования).

ЗАМЕЧАНИЕ. Сравнивая полученный здесь результат с результатом выбора по ИТ-критерию (без указанной γ(ЭТ)-модификации, см. пример 4.6 в гл. 4) видим, что оптимальный выбор, вообще говоря, изменился. Здесь модифицированный ИТ_γ(ЭТ)-критерий выбрал альтернативы X₂ и X₄ , в то время как ИТ-критерий (без указанной модификации) выбрал именно альтернативу X₄. Более того, подчеркнем, что в рамках модифицированного ИТ_γ(ЭТ)-критерия еще и альтернатива X₅ стала ранжироваться как более предпочтительная, по сравнению с альтернативой X₃ .

Вообще, в рамках рассмотренного здесь модифицированного ИТ_γ(ЭТ)-критерия анализируемые альтернативы ранжируются (по убыванию предпочтения) следующим образом:

X₂ и X₄, X₆, X₁ и X₅, X₃.

Легко видеть, что указанное ранжирование не совпадает с ранжированием по представленным ранее критериям принятия решений в условиях неопределенности. Естественно, для тех ЛПР, которые именно так и ранжировали бы указанные альтернативные решения, соответствующая модификация вполне могла бы соответствовать имеющейся системе предпочтений. Как видим, можно снова подчеркнуть, что менеджерам необходимо понимать особенность представленной здесь модификации ИТ_γ(ЭТ)--критерия и уметь использовать ее, чтобы более эффективно адаптировать линии уровня критерия применительно к системе предпочтений ЛПР.