3. Γ(ут)-модификация для критерия Гурвица (hWγ(ут)-критерий)

Представим особенности реализации соответствующих процедур γ(УТ)-модификации, которые обусловлены именно частичным сдвигом семейства линий уровня критерия (к утопической точке поля полезностей), применительно к HW-критерию Гурвица. Получаемый в результате такой модификации новый модифицированный критерий принятия решений в условиях неопределенности обозначаем кратко как HW_γ(УТ)-критерий.

Подчеркнем, что в такой ситуации алгоритм оптимизации альтернативного решения в рамках указанного HW_γ(УТ)-критерия можно характеризовать следующими шагами.

На начальном шаге (как и в предыдущем случае) уточняется конкретное значение коэффициента γ (), выбор которого (см. далее иллюстрацию в примере 6.2 - Дополнение) должен быть реализован ЛПР в соответствии со своей системой предпочтений в пространстве доходов. Кроме того, в соответствии с рекомендациями главы 2 формализуется значение приемлемого для ЛПР «весового» коэффициента С в рамках технологии критерия Гурвица. Дальнейшие процедуры можно представить следующими шагами.

Шаг 1. Применительно к исходной матрице полезностей, которую формализовали для соответствующей задачи оптимизации решения в условиях неопределенности, по формулам (*), (**) и (***) реализуются процедуры требуемой γ(УТ)-модификации. В результате получается новая модифицированная матрица полезностей.

Шаг 2. Для указанной новой модифицированной матрицы полезностей реализуются процедуры описанного в главе 2 HW-критерия Гурвица. Это означает, что к такой матрице дописываются три дополнительных столбца. А именно:

4. первый – для оценок по классическому ММ-критерию (напомним, что его элементы определяются как самые плохие, т.е. наименьшие, из возможных конечных экономических результатов при соответствующем решении);

5. второй – для оценок по классическому Н-критерию (напомним, что его элементы определяются как самые хорошие, т.е. возможные наибольшие конечные экономические результаты при соответствующем решении);

6. третий – для результирующих “взвешенных” оценок модифицированной матрицы по HW-критерию с учетом выбранных «весов» применительно к первым двум из указанных выше типов оценок.

Шаг 3. По элементам синтезированного третьего дополнительного столбца модифицированной матрицы полезностей определяется наилучшее / оптимальное альтернативное решение. А именно, это – решение, которому соответствует наилучший (наибольший) показатель в дополнительном столбце указанной матрицы.

Соответственно, в рамках рассматриваемого здесь HW_γ(УТ)-критерия семейство линий уровня критерия будет определяться равенствами типа:

Здесь

• К – показатель линии уровня;

• γ - выбранный ЛПР показатель коэффициента для «частичного» сдвига линий уровня критерия к утопической точке поля полезностей;

• ∆_α - соответствующие показатели (применительно к каждой координатной оси), добавление которых к аргументам критериальной функции, обеспечивает именно100%-ый сдвиг семейства линий уровня критерия к утопической точке поля полезностей ().

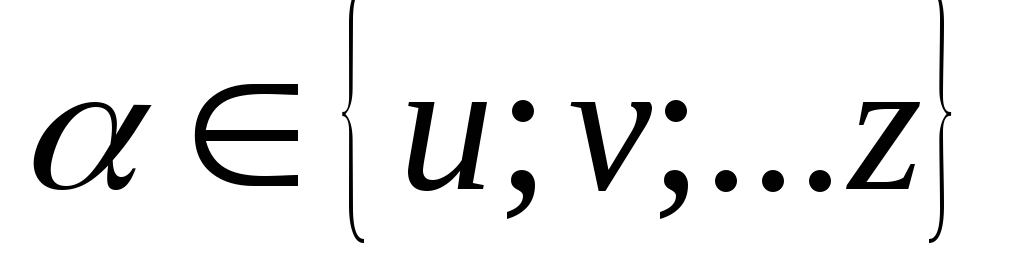Пусть

– вариант возможного решения ЛПР

– вариант возможной ситуации

– доход / прибыль для ЛПР, если будет принято решение i, а ситуация сложится j-ая;

– соответствующая исходная матрица полезностей для задачи оптимизации.

- требуемые «добавки» к элементам j-го столбца исходно матрицы полезностей при реализации процедур γ(УТ)-модификации (в рамках предпочтений ЛПР).

Тогда для целевой функции модифицированного HW_γ(УТ)-критерия имеем:

,

где

;

с - соответствующий “весовой” коэффициент, который выбирается ЛПР;

γ - соответствующий коэффициент для γ(УТ)-преобразования,

который адаптирован к предпочтениям ЛПР.

Графическая интерпретация для семейства линий уровня этого критерия, а также соответствующие особенности выбора оптимального решения, представлены на рис. 6.4 и 6.5.

Иллюстрацию численных процедур этого метода рассмотрим (для удобства сравнения результатов) на том же примере, который уже был использован выше.

ПРИМЕР 6.2. Для удобства изложения напомним исходные данные в рамках рассматриваемого примера. А именно, после формализации задачи принятия решений выделено множество из 4-х случайных событий, которые необходимо учитывать в рамках соответствующих решений. Кроме того, пусть анализируются 6 альтернативных решений , из которых требуется выбрать наилучшее. При этом соответствующая матрица полезностей имеет вид:

Решения	Доходы при событиях:
X1	5	4	3	3
X2	6	2	6	4
X3	-3	6	2	12
X4	3	9	1	5
X5	7	1	5	3
X6	6	6	1	4

Найдем наилучшее решение по модифицированному HW_γ(УТ)-критерию применительно к ситуации, когда, например, для «весового» коэффициента «с» в рамках технологии критерия Гурвица ЛПР выбирает значение с = 0,8. Кроме того, для более эффективной адаптации линий уровня такого критерия к своим предпочтениям ЛПР для параметра γ, в отличие от предыдущей модификации производного критерия Гурвица, выбирает значение γ= 0,4.

Шаг 1. Напомним, что соответствующая утопическая точка в поле полезностей применительно к этой задаче имеет координаты:

Х_У = (7; 9; 6; 12).

Максимальная координата этой точки, как видим, составляет 12. Далее, как и в примере 6.1, по формуле (*) определяем показатели для величин «сдвигов» по j-ой координатной оси в пространстве доходов (для случая 100%-ой реализации таких сдвигов). Они остаются прежними:

= 12 – 7 = 5; = 12 – 9 = 3;

= 12 – 6 = 6; = 12 – 12 = 0.

После этого определяем показатели с учетом требований ЛПР применительно к частичной реализации соответствующего сдвига (40% вместо 100% при указанных значениях ):

Показатели соответствующих сдвигов по координатным осям в пространстве доходов с учетом требований ЛПР применительно к частичной реализации соответствующего сдвига (40% вместо 100%) будут такими:

= 0,4∙5 = 2,0; = 0,4∙3 = 1,2;

= 0,4∙6 = 2,4; = 0,4∙0 = 0.

Поэтому, реализуя процедуры модификации, вполне аналогичные тем, которые были представлены в примере 6.1, с учетом формул перехода (****), получаем следующую модифицированную матрицу полезностей:

Решения	Доходы при событиях:
X1	7	5,2	5,4	3
X2	8	3,2	8,4	4
X3	-1	7,2	4,4	12
X4	5	10,2	3,4	5
X5	9	2,2	7,4	3
X6	8	7,2	3,4	4

Шаг 2. На этом шаге для указанной новой модифицированной матрицы полезностей реализуем процедуры представленного в главе 2 традиционно используемого на практике производного HW-критерия. Они определяют элементы трех дополнительных столбцов, которые дописываем к этой матрице. А именно, в первом выписаны показатели классической «крайней» пессимистической позиции (крайне осторожная позиция) для анализируемых решений. Во втором - представлены соответствующие показатели классической «крайней» оптимистической позиции для таких альтернатив. Наконец, в третьем столбце - синтезированный средневзвешенный показатель критерия Гурвица с учетом заданных «весов» для указанных крайних позиций в рамках модифицированной матрицы.

Решения	Доходы при событиях:				Показатель осторожной позиции	Показатель позиции оптимизма	Синтезированный показатель
							критерия
X1	7	5,2	5,4	3	3	7	0.8∙3+0,2∙7 =3,8
X2	8	3,2	8,4	4	3,2	8,4	0.8∙3,2+0,2∙8,4=4,24
X3	-1	7,2	4,4	12	-1	12	0.8∙(-1) +0,2∙12 =1,6
X4	5	10,2	3,4	5	3,4	10,2	0.8∙3,4+0,2∙10,2=4,76
X5	9	2,2	7,4	3	2,2	9	0.8∙2,2+0,2∙9 =3,56
X6	8	7,2	3,4	4	3,4	8	0.8∙3,4+0,2∙8 =4,32

Шаг 3. Находим самый большой элемент в третьем дополнительном столбце модифицированной матрицы полезностей. Он равен 4,76 (и выделен в дополнительном столбце матрицы). Соответствующее альтернативное решение (альтернатива X₄ ) является оптимальным выбором по модифицированному HW_γ(УТ)-критерию (при γ = 0,4 и с = 0,8).

ЗАМЕЧАНИЕ. Если сравнивать полученный здесь результат с результатом выбора по традиционному HW-критерию (без указанной γ(УТ)-модификации, - см., в частности, аналогичную модель примера 2.1) видим, что оптимальный выбор изменяется. А именно, здесь модифицированный HW _γ(УТ)-критерий выбрал альтернативу X₄, в то время как традиционный HW-критерий при том же весовом коэффициенте «с» будет выбирать альтернативу X₁. Более того, изменилось и ранжирование анализируемых альтернатив (по убыванию предпочтения):

X₄, X₆, X₂, X₁, X₅, X₃.

Это, естественно, обусловлено соответствующей модификацией, которая (при γ = 0,4) изменила линии уровня критерия, нацелив их «частично» на утопическую току поля полезностей. Такая модификация была реализована в соответствии с особенностями, которые были заданы ЛПР. Разумеется, снова требуется подчеркнуть, что менеджерам необходимо понимать специфику представленной здесь модификации HW-критерия Гурвица и уметь использовать ее, чтобы более эффективно адаптировать линии уровня критерия применительно к системе предпочтений ЛПР.

Как и в случае предыдущей модели, проиллюстрируем теперь соответствующие возможности для оценки приемлемых значений коэффициента γ () в рамках рассматриваемой модификации. При этом напомним, что возможности оценки и выбора параметра «с» (весового коэффициента для синтеза единого показателя критерия по указанным показателям двух крайних позиций) применительно к конкретным ЛПР в рамках критерия Гурвица уже были проиллюстрированы ранее в главе 2.