12. Приклади розв’язання типових задач з теми 11

Задача 1. Запишіть математичні вирази швидкостей прямого та зворотного процесів: 2СО_(г) + О_2(г)2 СО_2(г).

Як зміниться швидкість прямої реакції, якщо тиск у системі збільшити у 3 рази?

Розв’язання. Згідно із законом діючих мас (формула (11.1)), вираз швид-кості прямої реакції має вигляд

v_пр = k_пр С²(СО)С(О₂),

де k_пр  константа швидкості прямої реакції.

Швидкість зворотної реакції

v_зв= k_зв С²(СО₂),

де k_зв  константа швидкості зворотної реакції.

Позначимо концентрації вихідних речовин до зміни тиску в системі:

С(СО) = а; С(О₂) = b.

Тоді v_пр = k_пр а²b.

Згідно з рівнянням Менделєєва  Клапейрона

pV = nRT, (11.2)

де n = C(Х)V  кількість молів газу; С(Х)  молярна концентрація, моль/л;

R  універсальна газова стала (R = 8,31Дж/(моль·К)).

Підвищення тиску приводить до пропорційного збільшення концентрації кожного з газоподібних компонентів. Таким чином, після підвищення тиску в системі концентрація вихідних речовин становитиме:

С΄(СО) = 3а; С΄(О₂) = 3b.

Тоді швидкість прямої реакції

v΄_пр = k_пр (3а)² 3b = 27k_пр а²b;

.

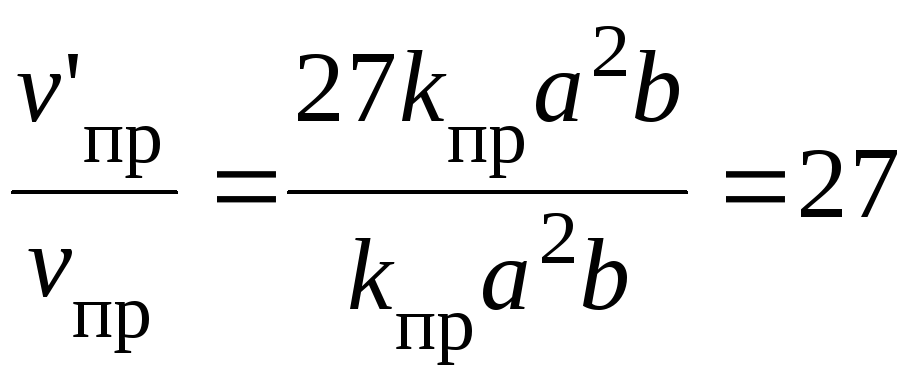Отже, з підвищенням тиску у три рази швидкість прямої реакції збільшиться у 27 разів.

Задача 2. У скільки разів і як зміняться швидкості прямої та зворотної реакцій у системі

2SO_2(г) + O_2(г)2SO_3(г),

якщо об’єм газової суміші збільшити у п’ять разів? У який бік зміститься рівновага у системі?

Розв’язання. Позначимо тиск газоподібних речовин до зміни об’єму системи:

р(SO₂) = a; р(О₂) = b; р(SO₃) = d.

Тоді згідно із законом діючих мас (формула (11.1)), швидкості прямої та зворотної реакцій становлять:

v_пр = k_пр а²b; v_зв = k_зв d².

Після збільшення об’єму гомогенної системи у п’ять разів тиск кожної з газоподібних речовин зменшиться теж у п’ять разів (формула (11.2)), тобто

р΄(SO₂) = (1/5)a; р΄(О₂) = (1/5)b; р΄(SO₃) = (1/5)d.

Тоді швидкості прямої та зворотної реакцій становитиме

v_пр = k_прb = k_пр а²b;

v_зв = k_зв= k_зв d².

Звідси

;

.

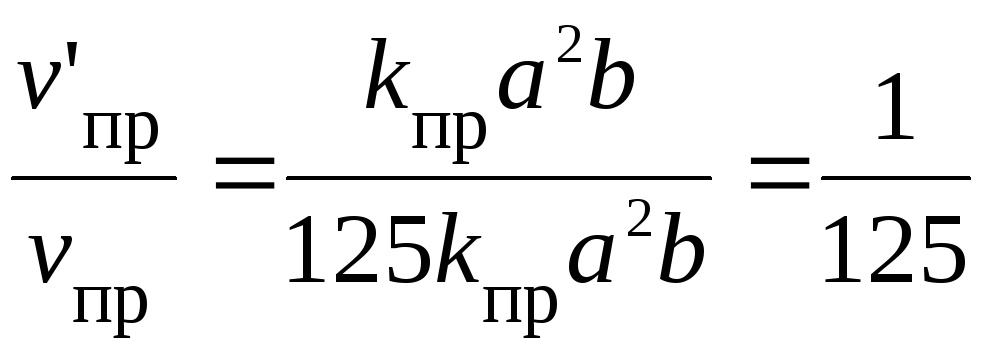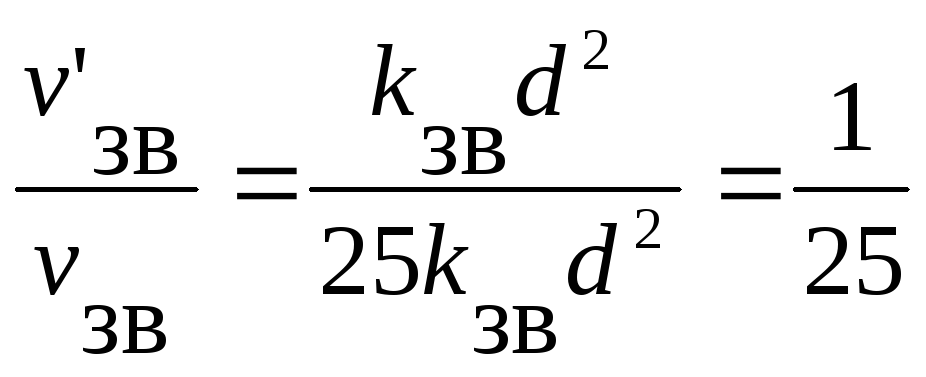Отже, швидкість прямої реакції зменшиться у 125 разів, а зворотної  тільки в 25 разів. При цьому рівновага у системі зміститься у бік зворотної реакції.

Задача 3. Обчисліть, у скільки разів збільшиться швидкість гомогенної реакції, яка проходить у газовій фазі, якщо температура зросте від 30 до 70 С, якщо температурний коефіцієнт швидкості реакції дорівнює двом.

Розв’язання. Математичний вираз правила Вант-Гоффа має вигляд

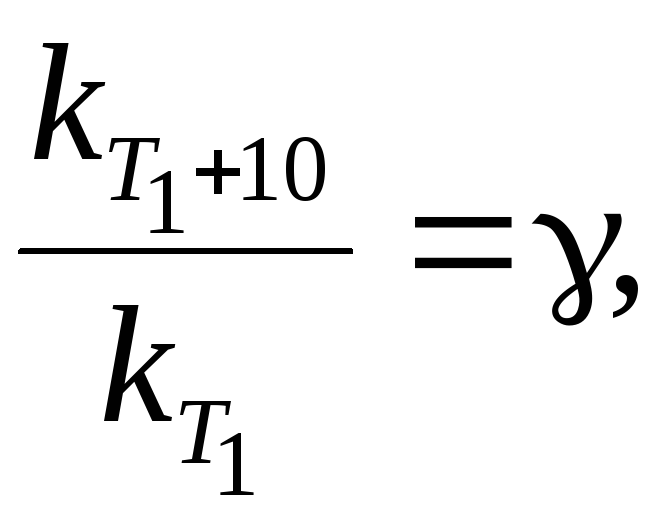 = 2…4,

де   температурний коефіцієнт швидкості реакції.

Якщо темпepатура змінюється на (n 10), то

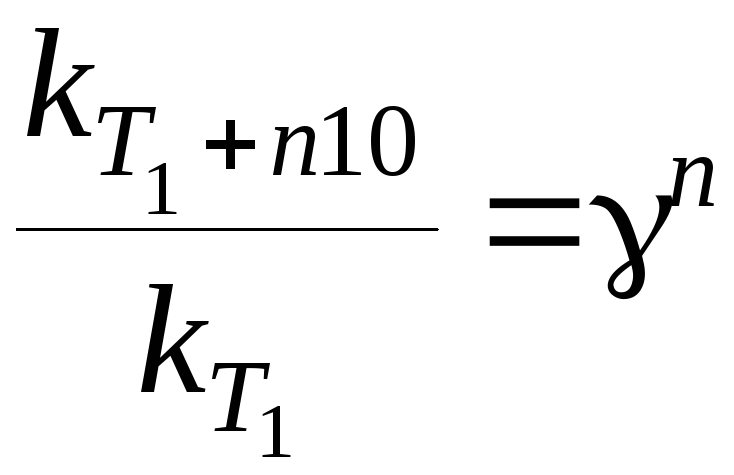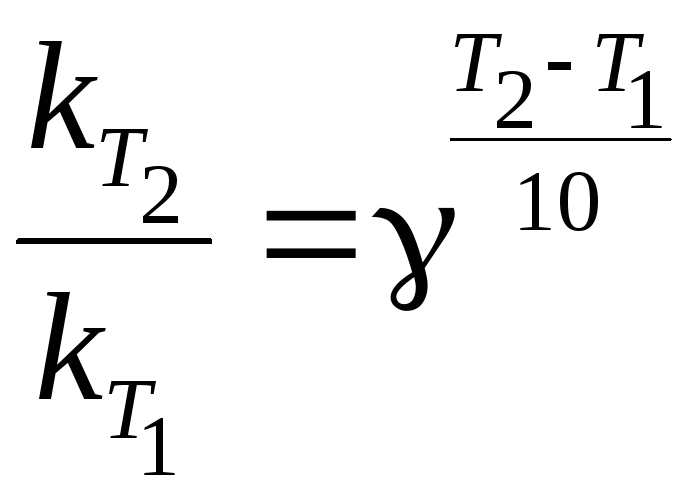або . (11.3)

Швидкість реaкції зростатиме зі збільшенням температури у стільки разів, у скільки зросте константа швидкості даної реакції. Для цієї реакції (враховуючи, що Т = t):

Отже, з підвищенням температури на 40 С швидкість даної реакції збільшиться у 16 разів.

Задача 4. Для деякої хімічної реакції константи швидкості при температурах 298 і 338 К дорівнюють k₂₉₈ = 0,01 і k₃₃₈ = 0,4 відповідно. Обчисліть температурний коефіцієнт швидкості реакції, константу швидкості при температурі 310 К та енергію активації цієї реакції.

Розв’язання. Температурний коефіцієнт швидкості реакції  можна визначити за формулою (11.3) після логарифмування:

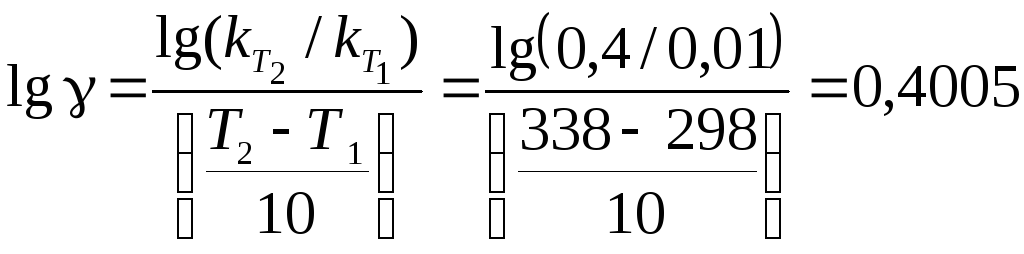;  = 2,51.

Визначаємо константу швидкості реакції при температурі 310 К (Т₃):

= 10^1,52 = 0,03.

За значеннями констант швидкості реакції при будь-яких двох температурах можна розрахувати енергію активації Е_А реакції за рівнянням Арреніуса:

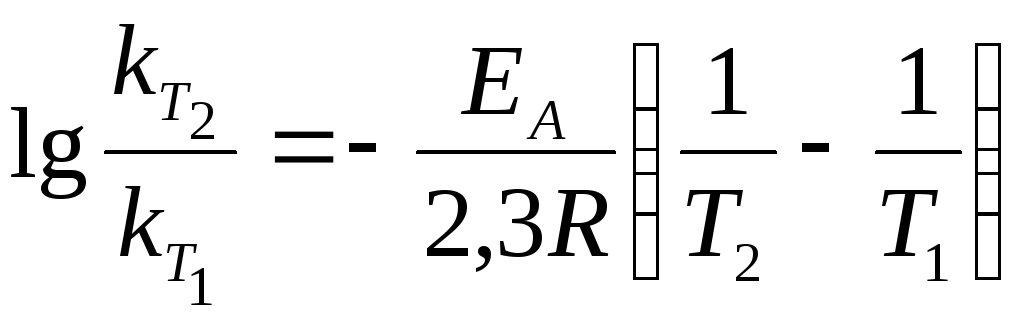; (11.4)

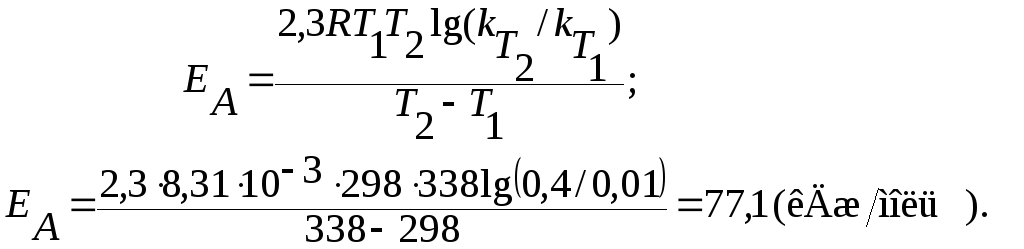(11.5)

Задача 5. Обчисліть, у скільки разів зменшиться швидкість деякої реакції під час зниження температури від 373 до 323 К, якщо енергія активації реакції становить 125,61 кДж/моль.

Розв’язання. Залежність константи швидкості реакції від температури описують формулою (11.4):

.

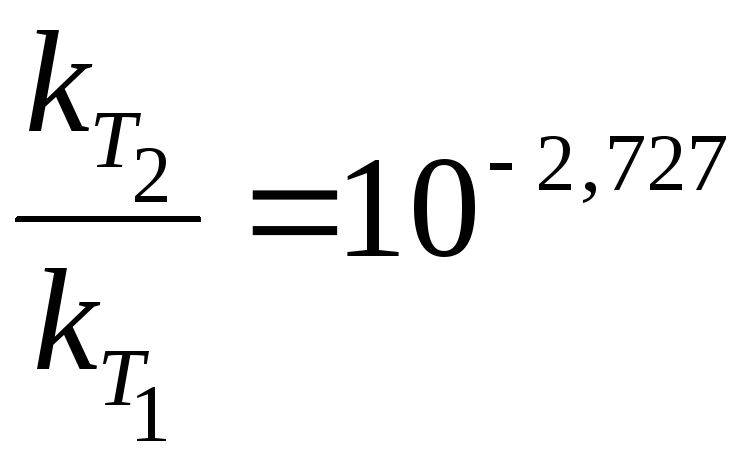
Отже, зі зниженням температури з 373 до 323 К швидкість реакції зменшиться у 534 рази.

Задача 6. З підвищенням температури з 298 до 398 К швидкість гетеро-генного процесу збільшилась у 25 000 разів. Обчисліть енергію активації реакції та визначіть, яка стадія процесу є лімітуючою: кінетична чи дифузійна.

Розв’язання. З рівняння Арреніуса (формула (11.5))

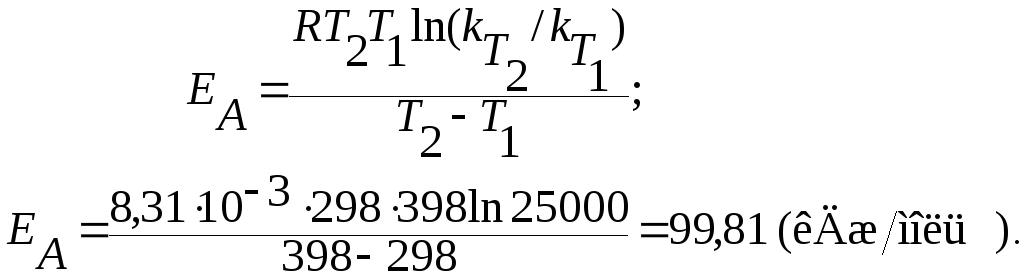
Відомо, що для кінетичних процесів (лімітуючою стадією є хімічна взаємодія)  лежить у межах 2…4, а E_A = 50…200 кДж/моль; тоді як для дифузійних процесів  = 1,1…1,4, а E_A = 5…20 кДж/моль. Обчислене значення енергії активації вказує на те, що лімітуючою стадією даного гетерогенного процесу є хімічна взаємодія.

Задача 7. Константа рівноваги реакції, поданої рівнянням:

CO_(г) + H₂O_(г)СО_2(г) + Н_2(г)

при 850 С дорівнює одиниці (K_р = 1). Визначіть рівноважні концентрації усіх речовин, якщо вихідні концентрації реагуючих речовин становлять

С_вих (СО) = 3 моль/л; С_вих (Н₂О) = 2 моль/л.

Розв’язання. У загальному вигляді для реакції

aA + bBeE + dD,

де всі речовини  гази, математичний вираз константи рівноваги має вигляд:

,

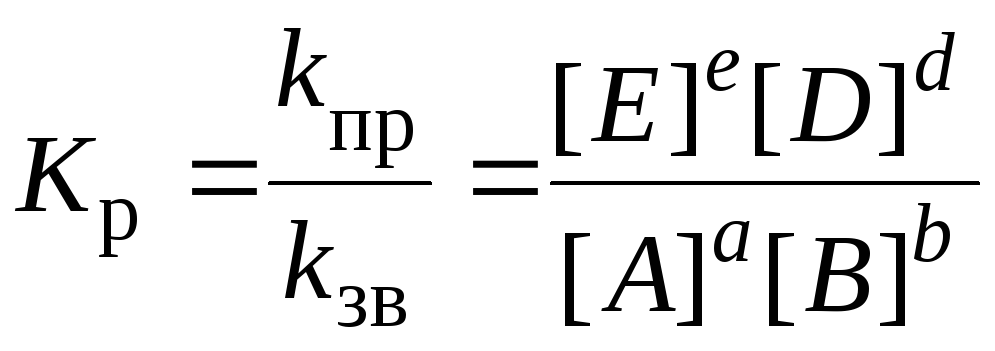де [А], [В], [Е], [D]  рівноважні молярні концентрації речовин, моль/л.

Запишемо закон діючих мас для прямої та зворотної реакцій:

v_пр = k_пр С(СО)С(Н₂О); v_зв = k_зв С(СО₂)С(Н₂).

У стані рівноваги v_пр = v_зв.

Для даної реакції математичний вираз константи рівноваги має вигляд:

.

Припустимо, що у стані рівноваги концентрація вуглекислого газу СО₂

становила х моль/л. Згідно з рівнянням реакції, концентрація водню Н₂ буде також х моль/л. На утворення х молів СО₂ і х молів Н₂ витрачають таку саму кількість молів (на 1 літр) СО і Н₂О. Отже, рівноважні концентрації усіх речовин становитимуть [CO₂] = [H₂] = х моль/л;[CO] = 3  х моль/л;

[H₂O] = 2  х моль/л.

Тоді

x² = 6  2x  3x + x²;

x = 1,2 (моль/л).

Таким чином, [CO₂] = [H₂] = 1,2 моль/л;[CO] = 3  1,2 = 1,8 моль/л;

[H₂O] = 2  1,2 = 0,8 моль/л.

Задача 8. Запишіть математичний вираз та розрахуйте значення кон-станти рівноваги реакції, поданої рівнянням:

FeO_(к) + CO_(г)Fe_(к) + CO_2(г) ,

якщо рівноважні молярні концентрації речовин становлять: [CO₂] = 0,05 моль/л; [CO] = 0,1 моль/л.

Розв’язання. Дана реакція  гетерогенна. Оскільки вона відбувається на поверхні поділу фаз, яка практично не змінюється у процесі, площу поверхні та концентрації твердих речовин можна вважати сталими. Тому у вираз константи рівноваги вводимо тільки рівноважні концентрації газів:

K_р = =

Задача 9. Обчисліть константу рівноваги реакції, поданої рівнянням:

Н_2(г) + I_2(г)2НI_(г),

якщо G⁰₂₉₈(HI) = 1,3 кДж/моль.

Розв’язання. Для даної реакції константа рівноваги має вигляд:

.

Вільну енергію Гіббса та константу рівноваги процесу зв’язує співвідношення

G⁰_х.р = RTlnK_р = 2,3RTlgK_р,

де G⁰_х.р  зміна вільної енергії Гіббса в хімічному процесі за стандартних умов, кДж.