методические указания лабораторных работ / Практическая РАБОТА 4 ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ НЕЧЕТКОЙ ЛОГИКИ

ПРАКТИЧЕСКАЯ РАБОТА № 4

ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ НЕЧЕТКОЙ ЛОГИКИ

Цель и содержание: Изучение теоретических основ и практическое применение методов нечеткой логики при решении плохо формализованных задач.

Теоретическое обоснование

При решении плохо формализованных задач могут быть использованы методы эволюционных вычислений и, в частности, генетические алгоритмы. При этом сравнительно тяжело проверить качество результата, полученного в процессе работы таких алгоритмов. Оценить степень качества результата решения плохо формализованной задачи можно с использованием методов нечеткой логики.

Нечеткая логика (fuzzy logic) — это надмножество классической булевой логики. Она расширяет возможности классической логики, позволяя применять концепцию неопределенности в логических выводах. В основе нечеткой логики лежит теория нечетких подмножеств (нечетких множеств). Эта теория занимается рассмотрением множеств, определяемых небинарными отношениями вхождения. Это означает, что принимается во внимание не просто то, входит элемент во множество или не входит, но и степень его вхождения, которая может изменяться от 0 до 1.

Нечеткое подмножество F может быть представлено, как отображение множества S на интервал I=[0, 1]. Это отображение определяется множеством упорядоченных пар: , , где s_i — i-й элемент множества S; n — мощность множества S; — степень вхождения элемента в множество F. Значение , равное 1, означает полное вхождение, указывает на то, что элемент s_i не принадлежит множеству F. Часто отображение задается функцией принадлежности x нечеткому множеству F. В силу этого термины «нечеткое подмножество» и «функция принадлежности» употребляются как синонимы. Степень истинности предиката «» определяется путем нахождения парному элементу s_k значения , определяющего степень вхождения s_k в F.

Обобщая геометрическую интерпретацию традиционного подмножества на нечеткий случай, получаем представление F точкой в гиперкубе Iⁿ, I=[0,1] (см. Рисунок A). В отличие от традиционных подмножеств точки, изображающие нечеткие подмножества, могут находиться не только на вершинах гиперкуба, но и внутри него.

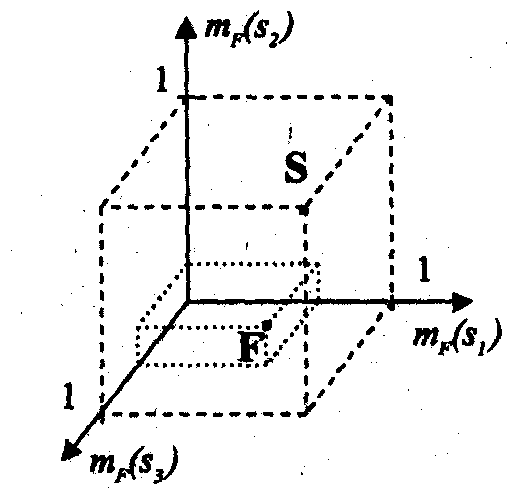
Рисунок A - Графическое представление нечеткого подмножества

Нечеткое правило логического вывода представляет собой упорядоченную пару (A, B), где A — нечеткое подмножество пространства входных значений X, B — нечеткое подмножество пространства выходных значений Y. Система нечеткого вывода — это отображение I^разм(X) в I^разм(Y), где разм(Z) — оператор определения пространства Z. Число элементов в I^разм(X) и I^разм(Y) бесконечно велико, поэтому не возможно задать правила нечеткого вывода соответствующими парами точек. Однако они могут быть описаны в терминах теории нечетких множеств. Нечеткие правила вывода образуют базу правил. Важно то, что в нечеткой экспертной системе в отличие от традиционной работают все правила одновременно, но степень их влияния на выход может быть различной. Принцип вычисления суперпозиции многих влияний на окончательный результат лежит в основе нечетких экспертных систем.

Процесс обработки нечетких правил вывода в экспертной системе состоит из 4 этапов:

1. Вычисление степени истинности левых частей правил (между "если" и "то") — определение степени принадлежности входных значений нечетким подмножествам, указанным в левой части правил вывода.

2. Модификация нечетких подмножеств, указанных в правой части правил вывода (после "то"), в соответствии со значениями истинности, полученными на первом этапе.

3. Объединение (суперпозиция) модифицированных подмножеств.

4. Скаляризация результата суперпозиции — переход от нечетких подмножеств к скалярным значениям.

Для определения степени истинности левой части каждого правила нечеткая экспертная система вычисляет значения функций принадлежности нечетких подмножеств от соответствующих значений входных переменных.

Полученное значение истинности используется для модификаций нечеткого множества, указанного в правой части правила. Для выполнения такой модификации используют один из двух методов: "минимума" и "произведения". Первый метод ограничивает функцию принадлежности для множества, указанного в правой части правила, значением истинной левой части (см. Рисунок B).

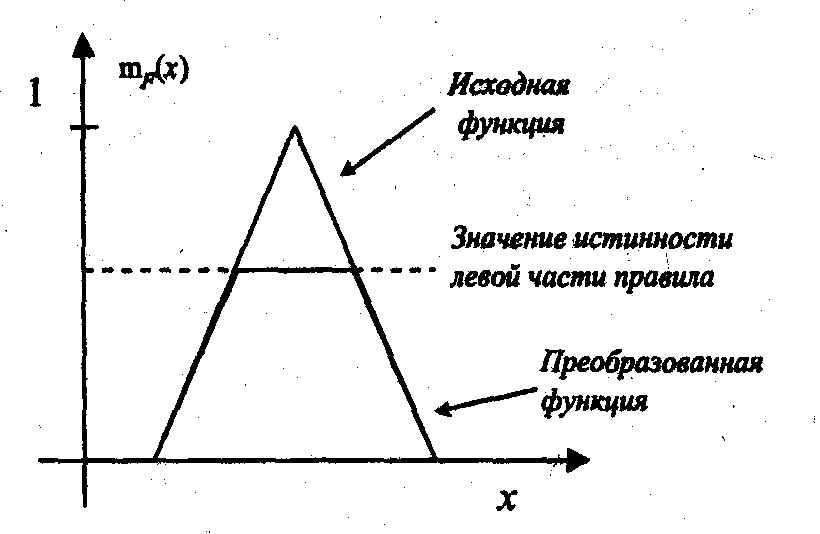
Рисунок B - Метод «минимума»

Во втором методе значение истинности левой части используется как коэффициент, на который умножаются значения функции принадлежности (см. Рисунок C).

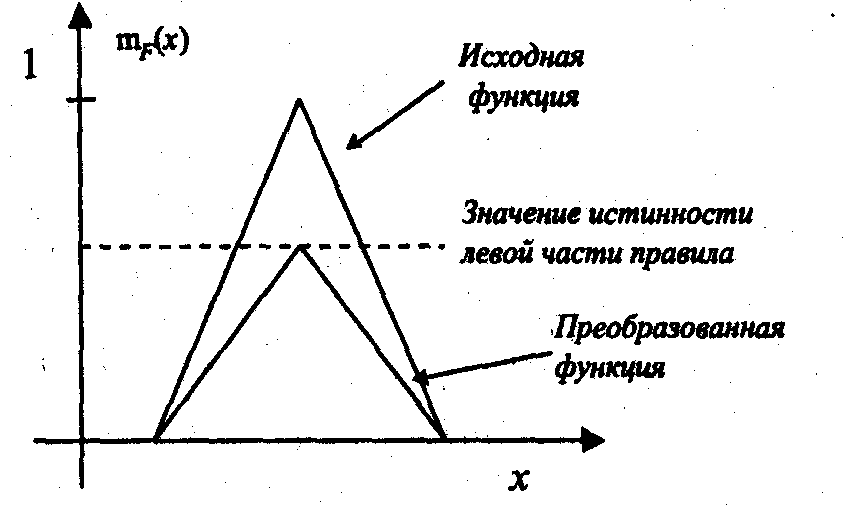
Рисунок C - Метод «произведения»

Результат выполнения правила — нечеткое множество, т.е. происходит ассоциирование переменной и функции принадлежности, указанных в правой части.

Выходы всех правил вычисляются нечеткой экспертной системой отдельно, однако в правой части нескольких из них может быть указана одна и та же нечеткая переменная. Для этого система производит суперпозицию нечетких множеств, связанных с каждой из таких переменных. Эта операция называется нечетким объединением правил вывода.

Традиционно суперпозиция функций принадлежности нечетких множеств определяется как . Графическое представление подобной суперпозиции представлено на Рисунок D.

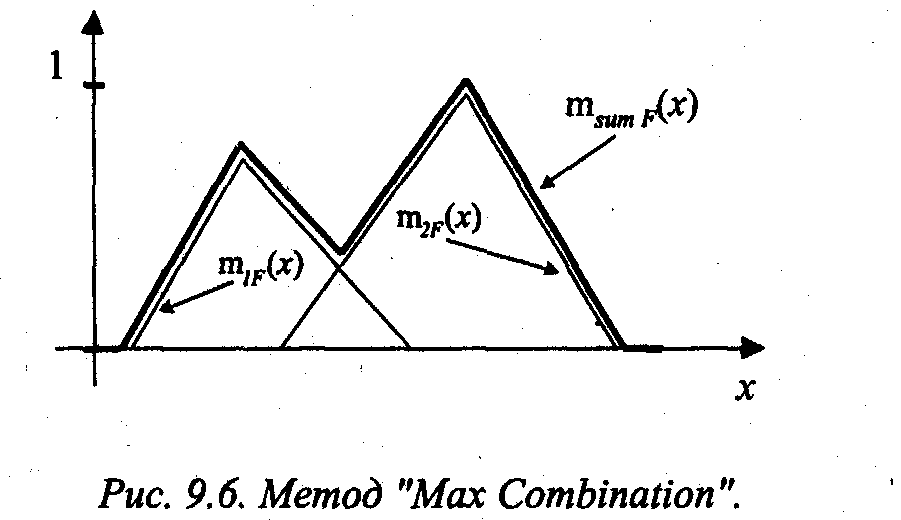
Рисунок D – Метод «Max Combination»

Другой метод суперпозиции состоит в суммировании значений всех функций принадлежности (графическая интерпретация приведена на Рисунок E): .

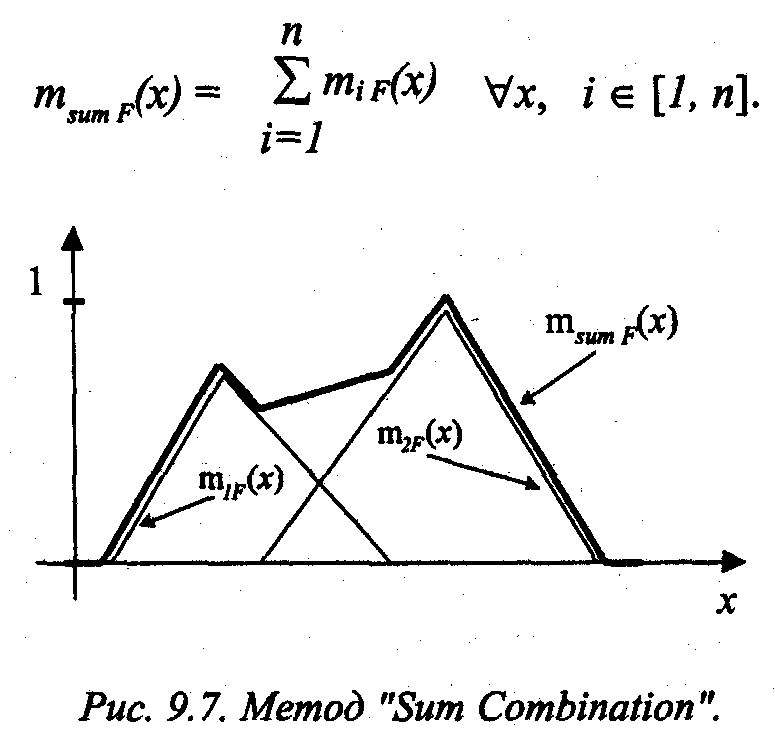
Рисунок E - Метод «Sum Combination»

Конечный этап обработки базы правил вывода — переход от нечетких значений к конкретным скалярным. Процесс преобразования нечеткого множества в единственное значение называется "скаляризацией" или "дефазификацией" (defuzzification). Чаще всего в качестве такого значения используется "центр тяжести" функции принадлежности нечеткого множества (centroid defuzzification method) (см. Рисунок F). Также допустима скаляризация методом «максимума» — выбор максимального значения суперпозиции функций принадлежности.

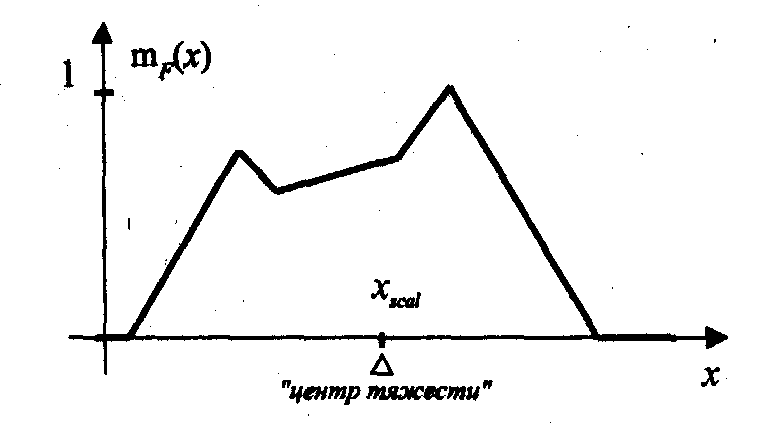
Рисунок F - Скаляризация методом «центра тяжести»

Методика выполнения работы

Продолжим рассмотрение предметной области «спортивные соревнования». Определим степень качества результата, полученного в предыдущей работе. Исходные данные к задаче представлены в Error: Reference source not found. Пусть спортивный клуб Локомотив признан «хорошим». Требуется спрогнозировать какое место по итогам соревнований он может занять, если в Error: Reference source not found, представлены промежуточные результаты.

Можно сформулировать следующие эвристические правила распределения мест среди спортивных клубов:

1. Если клуб наберет низкое количество очков, то займет «низкое» место.

2. Если клуб наберет среднее количество очков, то займет «среднее» место.

3. Если клуб наберет большое количество очков, то займет «большое» место.

Определим функции принадлежности, определенные на интервалах изменения количества очков для левых частей правил. Будем учитывать, что согласно сложившейся в турнирной таблице ситуации, количество набранных клубами очков может изменяться от 0 до 10.

Аналитически «низкое» количество очков представим как

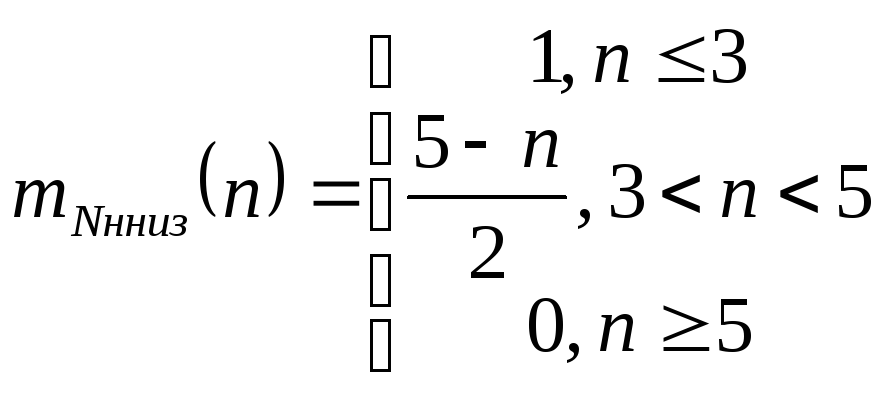
Графически данный факт представлен на Рисунок G

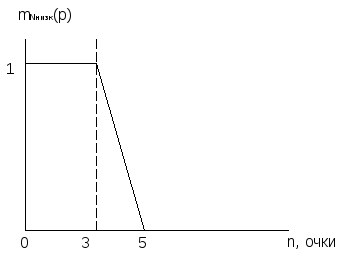
Рисунок G - Нечеткое подмножество "низкое", определенное на множестве значений количества очков

Количество очков «среднее» определим как

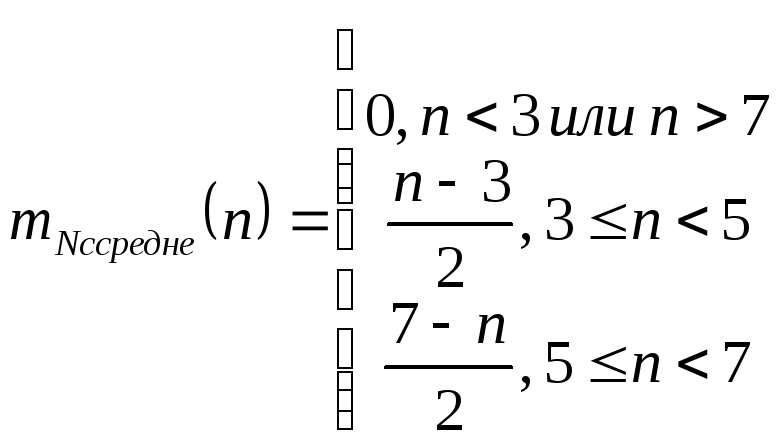
Графически данный факт представлен на Рисунок H.

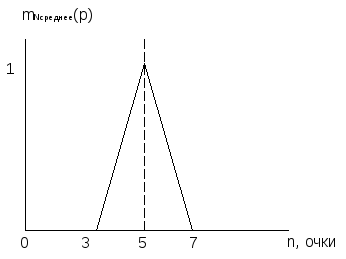
Рисунок H - Нечеткое подмножество "среднее", определенное на множестве значений количества очков

Количество очков «высокое» определим как

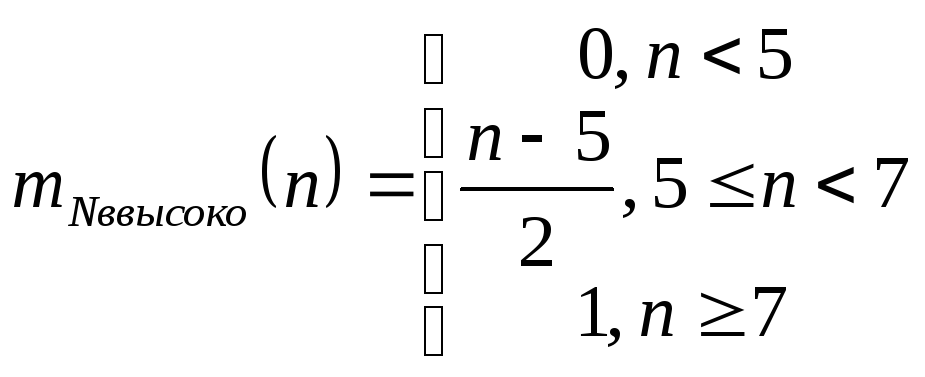
Графически данный факт представлен на Рисунок I.

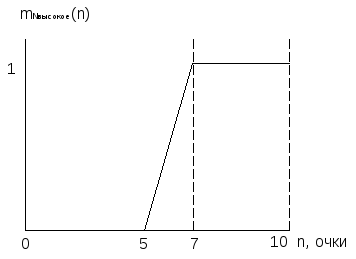
Рисунок I - Нечеткое подмножество "высокое", определенное на множестве значений количества очков

Определим нечеткие множества для занятого спортивным клубом места. Будем учитывать, что любой спортивный клуб может претендовать на место в диапазоне от 1 до 12. Для простоты интерпретации будем считать 12 место наилучшим, а 1 — наихудшим.

Аналитически «низкое» место представим как

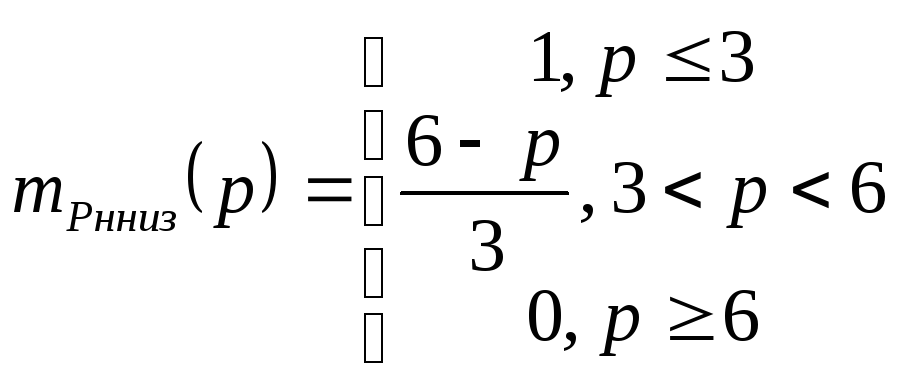
Графически данный факт представлен на Рисунок J.

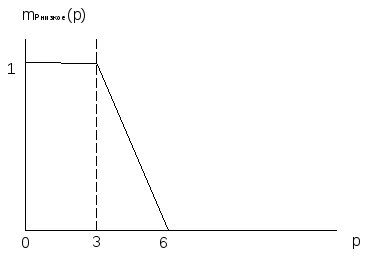
Рисунок J - Нечеткое подмножество "низкое", определенное на множестве значений мест

Количество очков «среднее» определим как

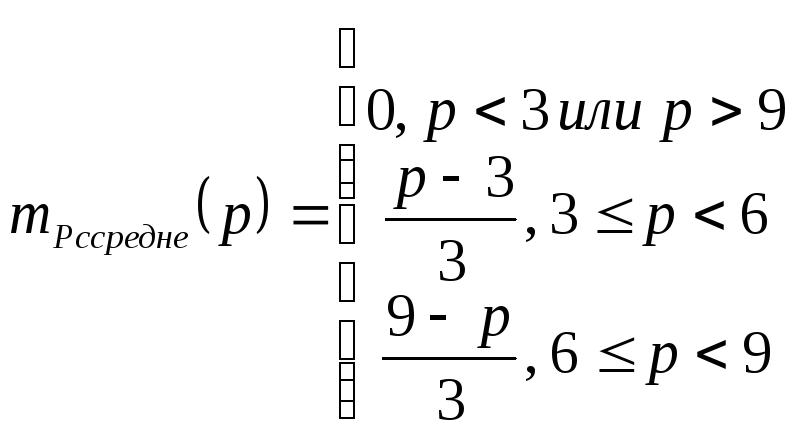
Графически данный факт представлен на Рисунок K.

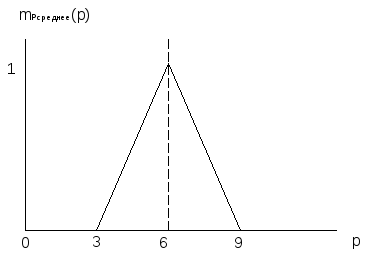
Рисунок K - Нечеткое подмножество "среднее", определенное на множестве значений мест

Место «высокое» определим как

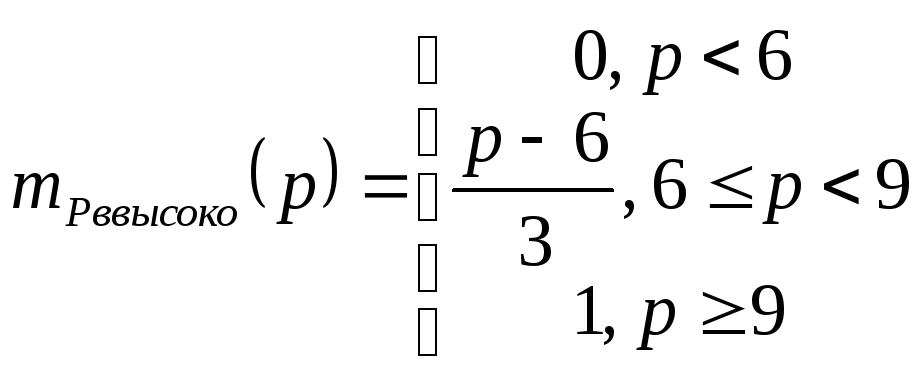
Графически данный факт представлен на Рисунок L.

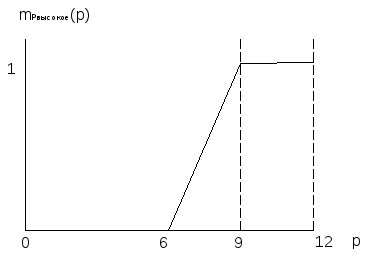
Рисунок L - Нечеткое подмножество "высокое", определенное на множестве значений мест

Вычислим степень истинности левых частей правил. Спортивный клуб Локомотив набрал 6 очков, и согласно функциям, представленным на Рисунок G, Рисунок H и Рисунок I имеем следующие значения функций принадлежности:

• ;

• ;

• .

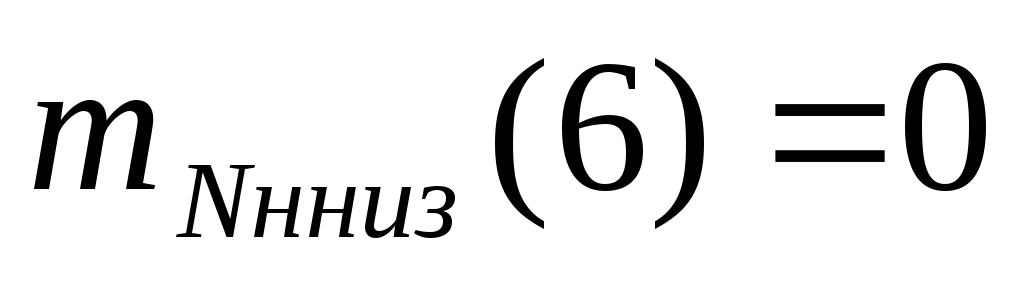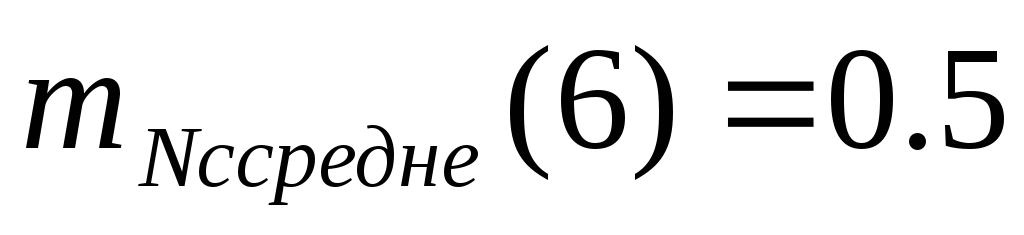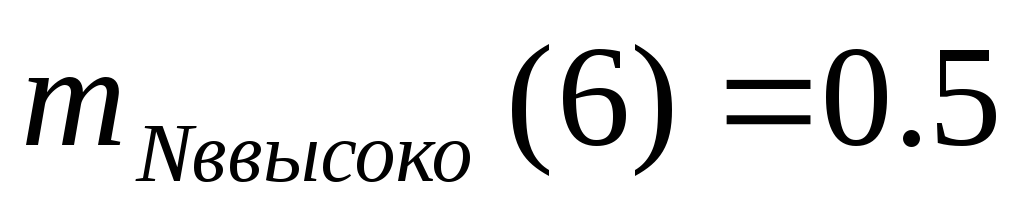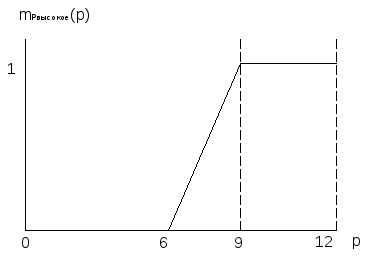
Значения истинности левой части каждого правила используется для модификации нечеткого множества, указанного в его правой части. Модификацию будем производить методом произведения (формально — умножаем соответствующие функции принадлежности, определенные на интервале занятых клубами мест на соответствующие значения истинности левых частей правил). На Рисунок M представлена описываемая ситуация.

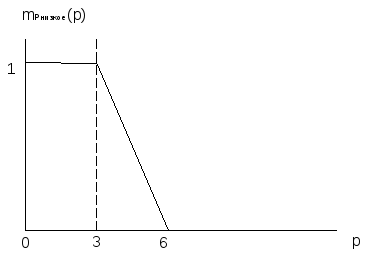* 0 =

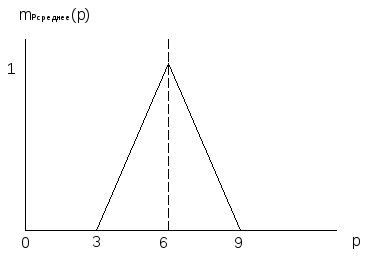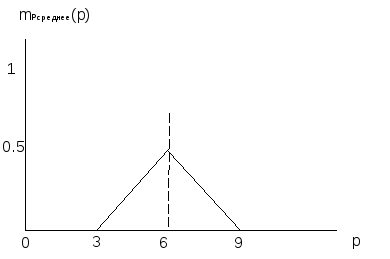
* 0.5 =

* 0.5 =

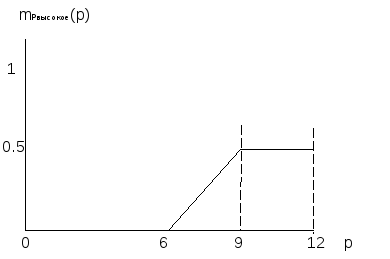
Рисунок M - Модификация нечетких множеств, определенных на интервале занимаемых клубами мест

Далее нечеткой экспертной системе необходимо обобщить результаты действия всех правил вывода, т.е. произвести суперпозицию полученных нечетких множеств. Воспользуемся для этого методом «Max Combination». Результат объединения нечетких множеств показан на Рисунок N.

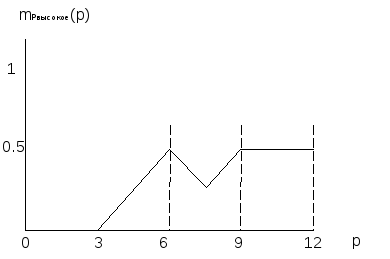
Рисунок N - Результат суперпозиции нечетких множеств

Теперь необходимо осуществить переход от суперпозиции множеств к скалярному значению. Скаляризацию произведем методом «центра тяжести». Иллюстрация полученного результата представлена на Рисунок O.

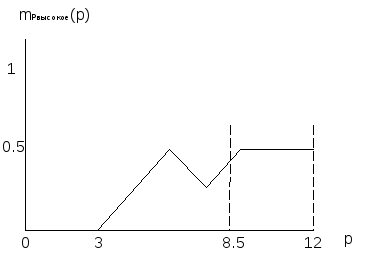
Рисунок O - Получение скалярного значения занятого места клубом Локомотив

Центр тяжести полученной фигуры (площади левой и правой части равны) находится в точке 8.5. Значит, клуб Локомотив может претендовать на место из интервала [8,9] или в стандартной интерпретации место из интервала [3,4].

Варианты заданий

Используя данные, полученные в результате выполнения предыдущей лабораторной работы определить степень качества полученного результата для каждого из двух ответов.

9