методические указания лабораторных работ / ПРАКТИЧЕСКАЯ РАБОТА №2 ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ

ПРАКТИЧЕСКАЯ РАБОТА №2

ТЕОРЕТИЧЕСКИЕ И ПРАКТИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ

Цель и содержание: Изучение теоретических основ и практическое применение генетических алгоритмов при решении плохо формализованных задач.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ

Большое количество современных практически значимых задач являются многокритериальными, то есть такими, в которых приходится учитывать большое число факторов. Здесь человеку приходится оценивать множество сил, влияний, интересов и последствий, характеризующих то или иное решение. Решения зачастую требуется принимать в режиме, близком к реальному времени.

Принятие решения в большинстве случаев заключается в генерации всех возможных альтернатив решений, их оценке и выборе лучшей среди них. Принять "правильное" решение - значит выбрать такой вариант из числа возможных, в котором с учетом всех разнообразных факторов и противоречивых требований будет оптимизирована некая общая ценность, то есть решение будет в максимальной степени способствовать достижению поставленной цели.

На сегодняшний день выделяют три основных типа методов поиска оптимальных решений:

1. методы, основанные на математических вычислениях;

2. перечислительные методы;

3. методы, использующие элемент случайности.

Первые два типа методов используют при решении хорошо формализованных задач, обладающих четкой формулировкой. Очевидный недостаток этих методов - очень жесткие условия, накладываемые на целевую функцию.

В основе методов третьего типа лежит случайный поиск в пространстве задачи с сохранением наилучшего полученного результата. Применение такого подхода не гарантирует получения оптимального решения. Вместе с тем следует заметить, что сейчас при решении очень сложных задач основной целью является поиск уже не оптимального, а более "хорошего" решения по сравнению с полученным ранее или заданным в качестве начального. Одним из типов таких "частично" случайных методов являются эволюционные вычисления.

Эволюционные вычисления - термин, используемый для описания алгоритмов поиска, оптимизации или обучения, основанных на некоторых формализованных принципах естественного эволюционного процесса. Основное преимущество эволюционных вычислений заключается в возможности решения многомодальных (имеющих несколько экстремумов) задач с большой размерностью за счет сочетания элементов случайности точно так, как это происходит в природной среде.

Генетические алгоритмы, являясь одной из парадигм эволюционных вычислений, представляют собой алгоритмы поиска, построенные на принципах, сходных с принципами естественного отбора и генетики. Они объединяют в себе принцип выживания наиболее перспективных особей - решений и структуризированный обмен информацией, в котором присутствует элемент случайности, который моделирует природные процессы наследования и мутации. Дополнительным свойством этих алгоритмов является невмешательство человека в развивающийся процесс поиска. Человек может влиять на него лишь задавая определенные параметры.

Генетический алгоритм работает с кодами, в которых представлен набор параметров, напрямую зависящих от аргументов целевой функции, безотносительно их смысловой интерпретации. Поэтому сам код и его структура описываются понятием генотип, а его интерпретация, с точки зрения решаемой задачи, понятием фенотип. Каждый код представляет точку пространства поиска. Экземпляр кода называют хромосомой, особью или индивидуумом.

На каждом шаге работы генетический алгоритм использует несколько точек поиска одновременно. Совокупность этих точек является набором особей, который называется популяцией. Количество особей в популяции называют размером популяции. В классических генетических алгоритмах размер популяции является фиксированным. На каждом шаге работы популяция обновляется путем создания новых особей и уничтожения старых. Чтобы отличать популяции на каждом из шагов и сами эти шаги, их называют поколениями и обычно идентифицируют по номеру. Например, популяция, полученная из исходной популяции после первого шага, будет первым поколением, после следующего шага — вторым, и т.д.

В процессе работы алгоритма генерация новых особей происходит на основе моделирования процесса размножения. При этом, естественно, порождающие особи называются родителями, а порожденные — потомками. Родительская пара, как правило, порождает пару потомков. Непосредственная генерация новых кодовых строк из двух выбранных происходит за счет работы оператора скрещивания, который также называют кроссинговером. При порождении новой популяции оператор скрещивания может применяться не ко всем парам родителей. Часть этих пар может переходить в популяцию следующего поколения непосредственно. Насколько часто будет возникать такая ситуация, зависит от значения вероятности применения оператора скрещивания, которая является одним из параметров генетического алгоритма.

Моделирование процесса мутации новых особей осуществляется за счет работы оператора мутации. Основным параметром оператора мутации также является вероятность мутации. Поскольку размер популяции фиксирован, то порождение потомков должно сопровождаться уничтожением других особей. Выбор пар родителей из популяции для порождения потомков производит оператор отбора, а выбор особей для уничтожения - оператор редукции. Основным параметром их работы является качество особи, которое определяется значением целевой функции в точке пространства поиска, описываемой этой особью.

К характеристикам генетического алгоритма относятся: размер популяции; оператор скрещивания и вероятность его использования; оператор мутации и вероятность мутации; оператор отбора; оператор редукции; критерий останова.

Операторы отбора, скрещивания, мутации и редукции называют еще генетическими операторами.

Критерием останова работы генетического алгоритма может быть одно из трех событий:

1. Сформировано заданное пользователем число поколений.

2. Популяция достигла заданного пользователем качества.

3. Достигнут некоторый уровень сходимости. То есть особи в популяции стали настолько подобными, что дальнейшее улучшение происходит очень медленно.

Характеристики генетического алгоритма выбираются таким образом, чтобы обеспечить малое время работы, с одной стороны, и поиск как можно лучшего решения, с другой.

Блок-схема работы генетического алгоритма представлена на Рис. 1.

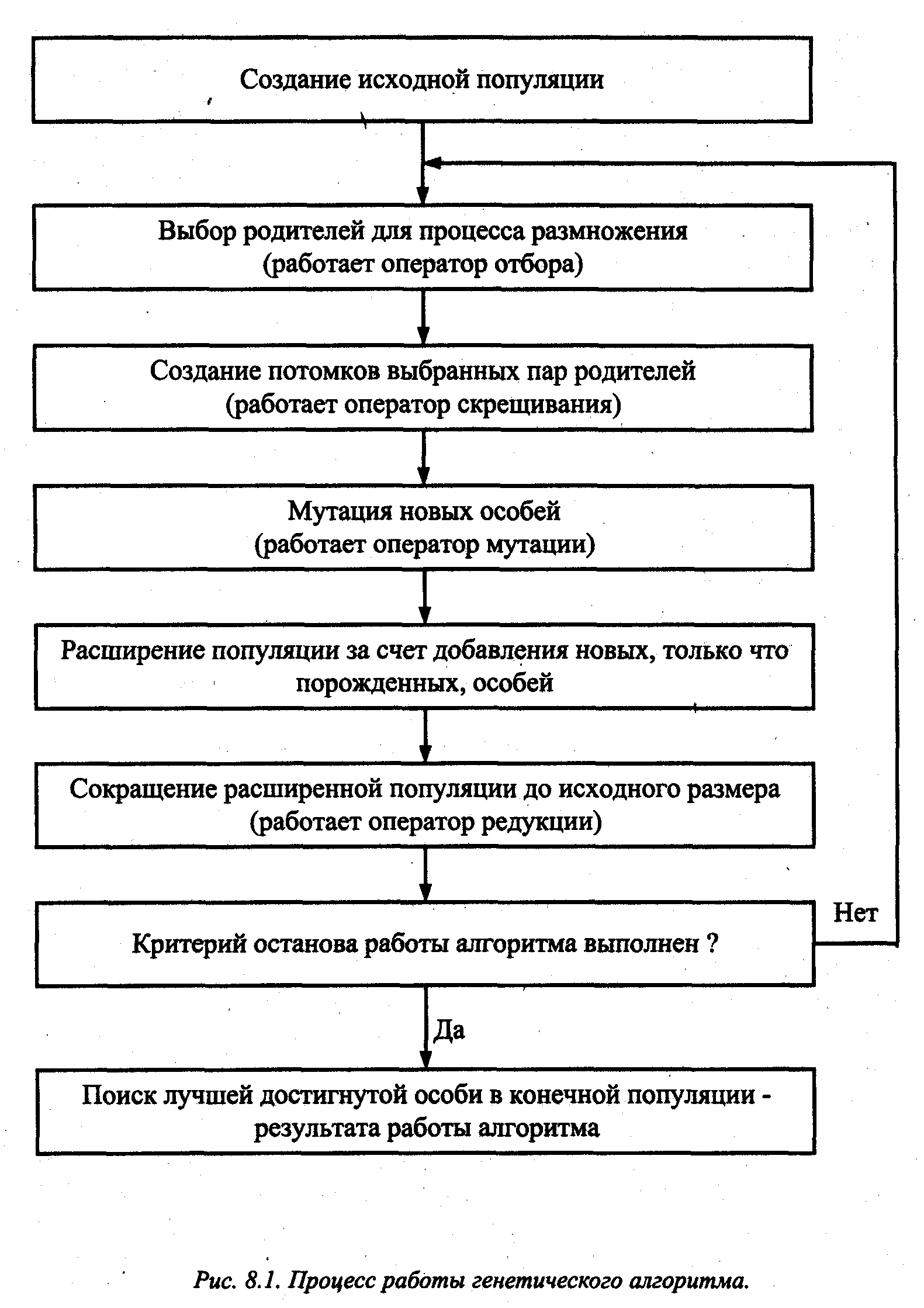
Рис. 1 - Блок-схема работы генетического алгоритма

Генетический алгоритм начинает свою работу с формирования исходной популяции с использованием какого-либо случайного закона, на основе которого выбирается нужное количество точек поискового пространства.

В основе оператора отбора, который служит для выбора родительских пар и уничтожения особей, лежит принцип "выживает сильнейший", например, случайный отбор особей. Вероятность участия особи в процессе размножения вычисляется по формул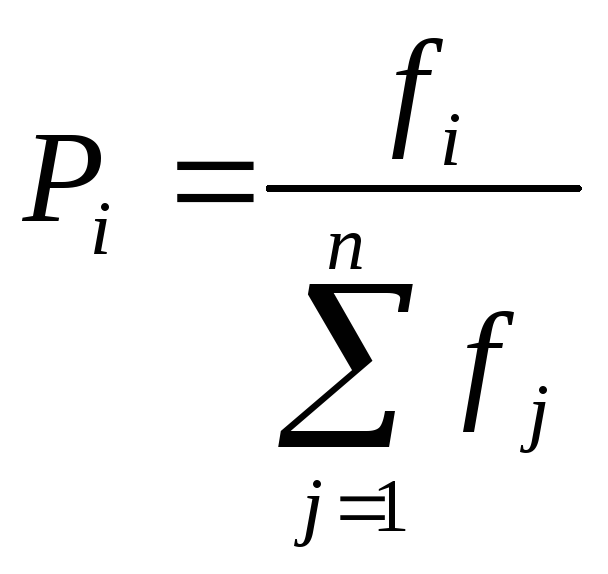е: , где - размер популяции, - номер особи, - вероятность участия особи в процессе размножения, - значение целевой функции для -й особи. Причем одна особь может быть задействована в нескольких родительских парах.

Аналогично может быть решен вопрос уничтожения особей. Только вероятность уничтожения должна быть обратно пропорциональна качеству особей. Однако обычно происходит просто уничтожение особей с наихудшим качеством.

Оператор скрещивания призван моделировать природный процесс наследования, то есть обеспечивать передачу свойств родителей потомкам. Простейший оператор скрещивания выполняется в два этапа. Пусть особь представляет собой строку из n элементов. На первом этапе равновероятно выбирается натуральное число k от 1 до . Это число называется точкой разбиения. В соответствии с ним обе исходные строки разбиваются на две подстроки. На втором этапе строки обмениваются своими подстроками, лежащими после точки разбиения, то есть элементами с -го по n-й. Так получаются две новые строки, которые наследовали частично свойства обоих родителей. Этот процесс можно представить как

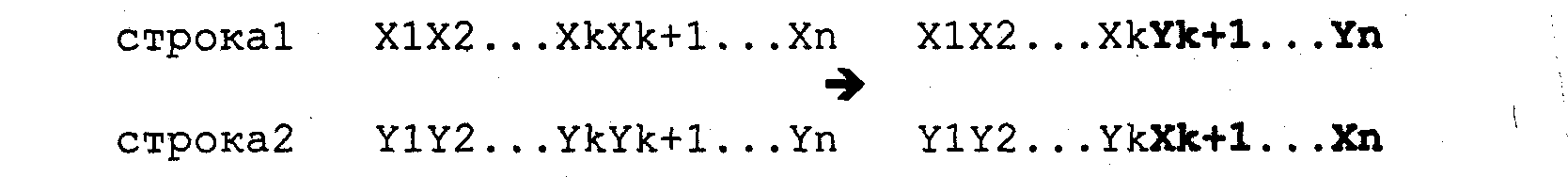
Вероятность применения оператора скрещивания обычно выбирается достаточно большой, в пределах от 0,9 до 1, чтобы обеспечить постоянное появление новых особей, расширяющих пространство поиска. При значении вероятности меньше 1 часто используют элитизм. Это особая стратегия, которая предполагает переход в популяцию следующего поколения элиты, то есть лучших особей текущей популяции, без всяких изменений. Применение элитизма способствует сохранению общего качества популяции на высоком уровне. При этом элитные особи также участвуют в процессе отбора особей для скрещивания. Количество элитных особей определяется обычно по формуле , где — количество элитных особей, — вероятность применения оператора скрещивания, — размер популяции.

Оператор мутации служит для моделирования природного процесса мутации. Его применение в генетических алгоритмах обусловлено следующими соображениями. Исходная популяция, какой бы большой она ни была, охватывает ограниченную область пространства поиска. Оператор скрещивания, безусловно, расширяет эту область, но все же до определенной степени, поскольку использует ограниченный набор значений, заданный исходной популяцией. Внесение случайных изменений в особи позволяет преодолеть это ограничение и сократить время поиска или улучшить качество результата. Вероятность мутации выбирается достаточно малой. Сам процесс мутации заключается в замене одного из элементов строки на другое значение. Это может быть перестановка двух элементов в строке, замена элемента строки значением элемента из другой строки и т.д.

В процессе работы алгоритма все указанные выше операторы применяются многократно и ведут к постепенному изменению исходной популяции. Поскольку операторы отбора, скрещивания, мутации и редукции по своей сути направлены на улучшение каждой отдельной особи, то результатом их работы является постепенное улучшение популяции.

После завершения работы генетического алгоритма из конечной популяции выбирается та особь, которая дает максимальное (или минимальное) значение целевой функции и является результатом работы генетического алгоритма.

МЕТОДИКА ВЫПОЛНЕНИЯ РАБОТЫ

Рассмотрим предметную область «спортивные соревнования». В таблице 1 представлены исходные данные задачи в виде турнирной сетки соревнований с указанием набранных спортивными клубами очков (данную таблицу можно реализовать в виде типа данных - структура, выбранного языка программирования).

Таблица 1 - Турнирная сетка спортивных соревнований

№ п/п	Название клуба	Очки
1.	Спартак	8
2.	Динамо	2
3.	Торпедо	4
4.	Сатурн	3
5.	Крылья Советов	3
6.	Металлург	9
7.	ЦСКА	7
8.	Локомотив	6
9.	Зенит	1
10.	Сокол	1
11.	Ростсельмаш	7
12.	СКА	5

Определим при заданных условиях два «хороших» спортивных клуба. При этом не ставится задача поиска двух наилучших клубов (в нашем случае ими является пара {Спартак, Металлург}), но требуется определить два не самых плохих клуба. Таким образом, мы соглашаемся на компромисс, при котором результат работы алгоритма будет непредсказуемым при каждом запуске: всякий раз могут быть отобраны два произвольных клуба с «немалым» количеством очков.

Решим представленную задачу с использованием генетического алгоритма.

1. Определим особь в виде двойки названий клубов: {Название1, Название2}. Особи формируются случайным образом, но с учетом постановки задачи: Название1<>Название2.

2. Определим размер популяции - 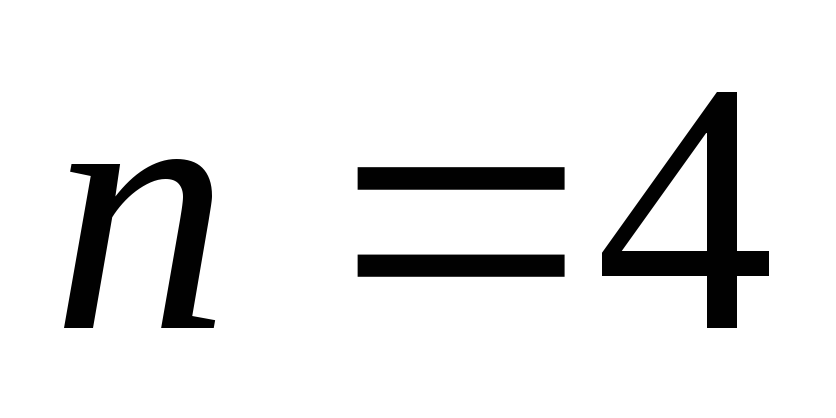особи. Таким образом, единовременно алгоритмом будут обрабатываться максимум 8 клубов.

3. Оставшиеся клубы могут быть включены в работу алгоритма посредством срабатывания оператора мутации, т.е. в исходную популяцию будут добавляться особи вида {Название1’, Название2’}, где Название1’ и Название2’ взяты из числа клубов, отсутствующих в существующей на данный момент популяции. Определим вероятность срабатывания оператора мутации - 5%.

4. Элитизм не используется.

5. В качестве целевой функции будем использовать сумму очков двух клубов особи: 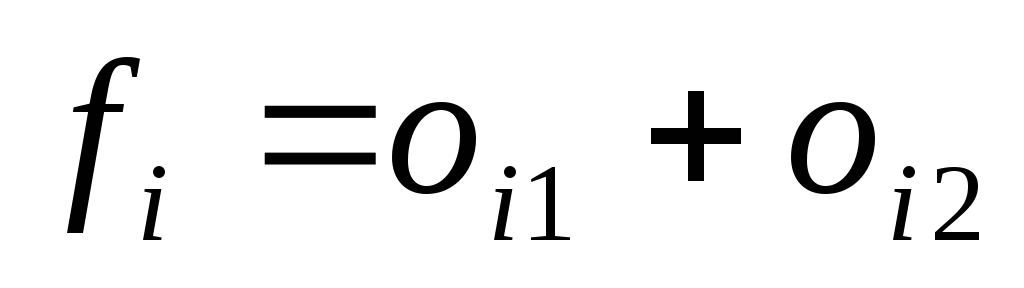, где 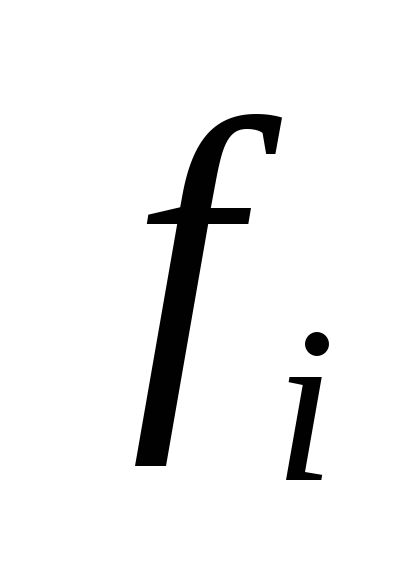— значение целевой функци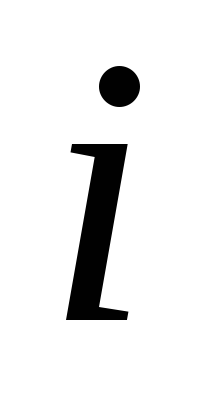и -й особи, (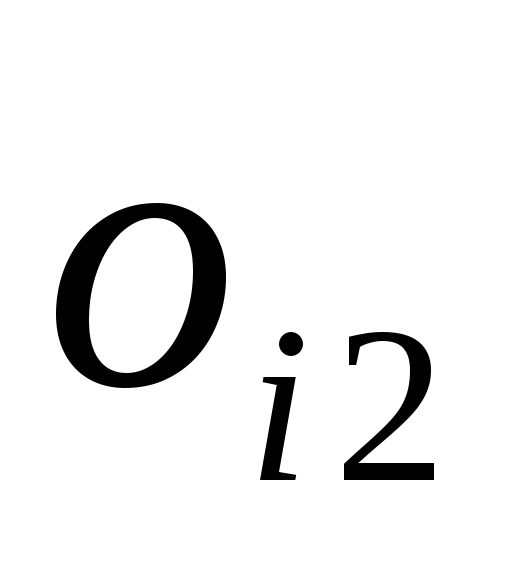) — число очков первого (второго) клуба 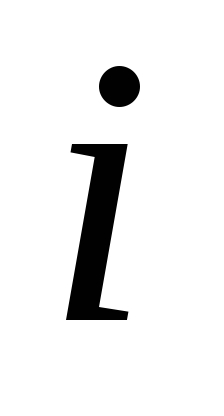-й особи.

6. В качестве оператора скрещивания будем использовать его простую интерпретацию в виде обмена подстроками (названиями вторых клубов) двух родительских особей, при этом следует учитывать, что для новых особей должно выполняться условие Название1<>Название2.

7. Оператор редукции будет уничтожать наихудшие особи.

8. Критерием останова алгоритма будет формирование двух поколений.

Пусть случайным образом на первом шаге формируется популяция, представленная в Таблица 2е 2.

Таблица 2 - Исходная популяция

№ п/п	Особь		Вероятность участия в размножении	Выбор родителей
1.	Спартак, Торпедо	12	12/42
2.	Ростсельмаш, ЦСКА	14	14/42	*
3.	Динамо, СКА	7	7/42
4.	Сатурн, Локомотив	9	9/42	*

Качество исходной популяции определим как . Пусть на основе вероятностей участия в размножении особей популяции в качестве родительских случайным образом выбраны особи {Ростсельмаш, ЦСКА} и {Сатурн, Локомотив}. После выполнения оператора скрещивания получим две новые особи {Ростсельмаш, Локомотив} со значением целевой функции и {Сатурн, ЦСКА} со значением целевой функции . Пусть оператор мутации не сработал. Среди шести особей полученной популяции первого поколения оператор редукции уничтожит две наиболее слабые: {Динамо, СКА} c и {Сатурн, Локомотив} c . В итоге получим популяцию первого поколения, представленную в Таблица е 3.

Таблица 3 - Популяция первого поколения

№ п/п	Особь		Вероятность участия в размножении	Выбор родителей
1.	Спартак, Торпедо	12	12/49	*
2.	Ростсельмаш, ЦСКА	14	14/49	*
3.	Ростсельмаш, Локомотив	13	13/49
4.	Сатурн, ЦСКА	10	10/49

Качество полученной популяции выше качества исходной популяции с . На втором шаге в результате работы оператора скрещивания появятся две новые особи {Спартак, ЦСКА} c и {Ростсельмаш, Торпедо} c . Пусть, не смотря на низкую вероятность, сработал оператор мутации и в текущую популяцию случайным образом добавилась особь {Металлург, СКА} с . Среди семи особей полученной популяции второго поколения оператор редукции уничтожит три наиболее слабые: {Сатурн, ЦСКА} c , {Ростсельмаш, Торпедо} c и {Спартак, Торпедо} c . После второго шага достигнут критерий останова работы генетического алгоритма. В итоге получим популяцию второго поколения, представленную в Таблица 4е 4.

Таблица 4 - Популяция второго поколения

№ п/п	Особь
1.	Ростсельмаш, ЦСКА	14
2.	Ростсельмаш, Локомотив	13
3.	Спартак, ЦСКА	15
4.	Металлург, СКА	14

Качество полученной популяции , что превосходит качество всех предыдущих популяций. Из числа последних особей выбирается особь с наилучшими характеристиками, в данном случае «хорошими» спортивными клубами являются Спартак и ЦСКА.

ВАРИАНТЫ ЗАДАНИЙ ДЛЯ САМОСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

Вариант 1. Предметная область «учебный процесс»: специальность вуза имеет учебный план с перечнем дисциплин по каждой, из которой известна трудоемкость в часах. Определить три «сложные» дисциплины учебного плана.

Вариант 2. Предметная область «поликлиника»: существует реестр больных, обратившихся в поликлинику с указанием числа обращений. Определить трех «очень больных» посетителей поликлиники.

Вариант 3. Предметная область «библиотека»: существует реестр книг, хранящихся в библиотеке с указанием числа выдач клиентам. Определить три «популярные» книги библиотеки.

Вариант 4. Предметная область «автосервис»: существует реестр марок автомобилей, прошедших ремонт в автосервисе с указанием числа поломок. Определить три «надежные» марки автомобилей.

Вариант 5. Предметная область «билетная касса»: существует реестр маршрутов с указанием числа купленных билетов. Определить три «популярные» маршрута.

Вариант 6. Предметная область «спортивные соревнования»: существует реестр спортивных клубов с указанием суммарного числа спортсменов. Определить три «популярные» спортивные клуба.

Вариант 7. Предметная область «телефонная станция»: существует реестр номеров телефонной станции с указание суммарного числа дозвонов на них. Определить три «загруженные» телефонные номера.

Вариант 8. Предметная область «магазин»: существует реестр товаров магазина с указанием числа покупок. Определить три «покупаемые» товары.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Для чего используется концепция элитизма? Привести пример для предметной области «спортивные соревнования».

2. В чем заключается отличие эволюционных вычислений от традиционных методов поиска?

3. Пояснить назначение основных блоков блок-схемы генетического алгоритма.

4. Каково назначение оператора отбора? Предложить собственный оператор отбора.

5. Какова область применения генетических алгоритмов?

10