Содержание работы

1. Прямая линия на плоскости

2. Кривые второго порядка

3. Полярная система координат

4. Векторная функция скалярного аргумента

Литература [1,7,17]

Замечания преподавателя

Прямая линия на плоскости

1. Точка является вершиной квадрата, одна из сторон которого лежит на прямой линии . Вычислить площадь квадрата.

2. Найти точку пересечения медиан треугольника, вершинами которого являются точки .

3. Записать уравнение прямой, проходящей через начало координат и образующей угол с прямой линией .

4. Точка является вершиной квадрата, диагональ которого лежит на прямой 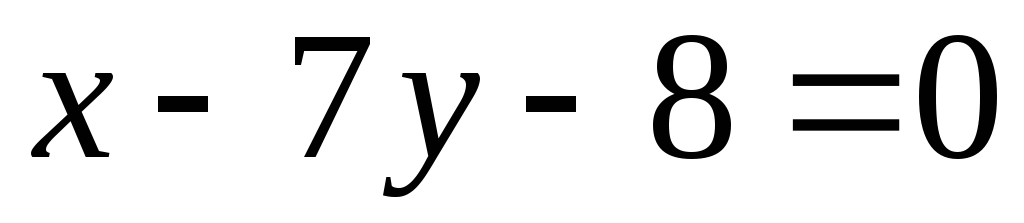. Написать уравнения сторон и второй диагонали этого квадрата.

5. Кривые второго порядка

а) Постройте кривые и укажите их основные характеристики

; ;

б) Установите, какие линии определяются уравнениями и схематично их постройте:

• 

• 

• 

• 

• 

Примечание. В последнем случае используйте поворот системы координат на угол согласно соотношениям

6. Найдите координаты фокуса параболы по координатам ее вершины и уравнению ее директрисы .

Ответ:

7. На гиперболе найти точку, ближайшую к точке

8.Векторная функция скалярного аргумента. Векторы скорости и ускорения. Кривизна плоской кривой.

а). По уравнению движения определите траекторию движения (годограф), вектор скорости , вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов и .

б) По уравнению движения определите траекторию движения (годограф), вектор скорости, вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов и .

в). Найдите кривизну в вершинах эллипса в вершинах эллипса.

9.Полярная система координат:

а) Постройте кривые в полярной системе координат:

, , _,

_{б) Найти площадь фигуры, ограниченной какой-либо кривой, указанной в предыдущем задании}

в) Найдите длину дуги кривой

Контрольные вопросы

1. Линейные операции над векторами

2. Векторный базис в пространстве n-измерений. Условия существования базиса.

3. Прямоугольный декартов базис. Координаты вектора в этом базисе. Модуль вектора.

4. Направляющие косинусы. Единичный вектор (орт).

5. Скалярное произведение векторов. Определение. Свойства. Вычисление.

6. Векторное произведение векторов. Определение. Свойства. Вычисление.

7. Смешанное произведение векторов. Определение. Свойства. Вычисление.

8. Уравнения прямой на плоскости: с направляющим вектором, через две точки, в «отрезках на осях », с угловым коэффициентом. Общее уравнение прямой.

9. Канонические уравнения и характеристики кривых второго порядка

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

Направление подготовки 140400.62

«Электроэнергетика и электротехника»