-
Раскрыть неопределенности:
7.Написать формулы для приближенного вычисления интегралов при помощи разложения функций в степенной ряд. Указать область сходимости ряда.
Контрольные вопросы
1.Числовой ряд. Определение суммы ряда
-
Ряд из членов геометрической прогрессии. Условия сходимости. Приведите примеры.
-
Необходимый признак сходимости числового ряда. Гармонический ряд
-
Критерий сходимости числового ряда с неотрицательными членами
-
Достаточные условия сходимости ряда. Признак сравнения
-
Достаточные условия сходимости ряда. Признак Даламбера
-
Достаточные условия сходимости ряда. Признак радикальный Коши
-
Достаточные условия сходимости ряда. Интегральный признак. Условия сходимости ряда
-
Теорема Тейлора. Формула Маклорена. Ряд Тейлора. Ряд Маклорена.
-
Получите разложение в ряд Маклорена для функции
-
Получите разложение в ряд Маклорена для функции
-
4.Получите разложение в ряд Маклорена для функции
-
Чему равен коэффициент
разложения функции
в ряд Тейлора по степеням
-
Интервал сходимости ряда
равен
.
Сумма
-
Чему равна производная порядка
в точке
функции
? -
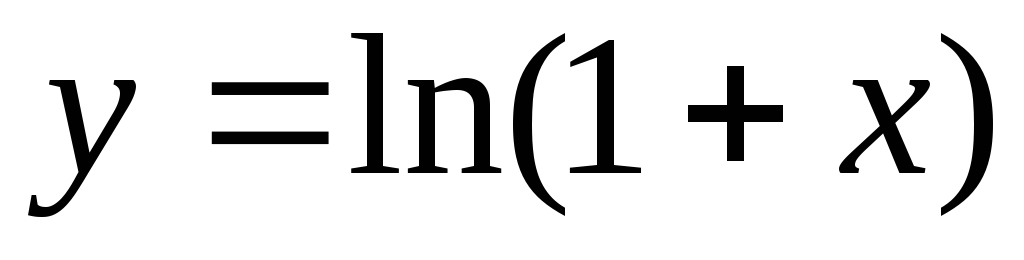Как определить степенной порядок малости при помощи разложения в ряд Тейлора в окрестности точки ? Приведите примеры.
-
Как можно определить степенной порядок роста бесконечно большой в окрестности точки разрыва 2 рода?
-
Что называют наклонной (горизонтальной) асимптотой графика функции? Какие способы нахождения асимптот Вы знаете? Как использовать теорему Тейлора для нахождения асимптот? Приведите примеры.
Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет»
Направление подготовки 140400.62
«Электроэнергетика и электротехника»
Математика
Самостоятельная работа
РГР № 6 (0,278 ЗЕ)
Применение производной к исследованию функций
Срок выполнения 9-12 неделя
Выполнил студент группы ЭА- 111
Петров А.В.
Работу принял
Кемерово 2011
Содержание работы
-
Полное исследование функции и построение графика
-
Раскрытие неопределенностей с использованием правила Лопиталя
-
Задачи на наибольшее и наименьшее значения функции
Литература [1,2,8,17]
Замечание преподавателя
1. Провести полное исследование и построить графики функций (область определения, четность, нули функции, точки разрыва, вертикальные асимптоты, поведение при больших значениях аргумента – наклонные и горизонтальные асимптоты, локальные экстремумы, точки перегиба) (построить 2 функции по заданию преподавателя):
,
,
,
2. Найдите наибольшее и наименьшее значения функции на отрезке:
а)
,
б)
3.
Написать приближенные
формулы, описывающие поведение функций
вблизи точек локальных экстремумов и
точек перегиба
, 
4. Раскрыть неопределенности, используя правило Лопиталя:
5. Решите задачи (две задачи по выбору)
а) Найти
угловой коэффициент прямой, проходящей
через точку
и
отсекающей от координатных осей
треугольник наименьшей
площади
(
.
б) Объем
правильной треугольной призмы
.
Какова должна быть сторона основания,
чтобы полная поверхность была наименьшей?
в) В треугольник
с основанием
и высотой
вписать прямоугольник с наименьшим
периметром.
г) В шар радиуса
вписать
цилиндр наибольшего объема
д) Около заданного шара описать конус наименьшего объема
Контрольные вопросы
-
Сколько асимптот имеет график функции
,
,
? -
Дайте определение точки локального экстремума функции
-
Сформулируйте необходимые условия существования экстремума
-
Сформулируйте достаточные условия существования экстремума
-
Дайте определение точки перегиба графика функции и сформулируйте необходимые условия его существования
Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет»
Направление подготовки 140400.62
«Электроэнергетика и электротехника»