Математика
Самостоятельная работа
РГР № 3 (0,417 ЗЕ)
Основные методы интегрирования
Срок выполнения 3-4 недели
Выполнил студент группы ЭА- 111
Петров А.В.
Работу принял
Кемерово 2011
Содержание работы
-
Таблица интегралов
-
Замена переменной
-
Интегрирование дробно-рациональных и иррациональных функций
-
Интегрирование по частям
-
Интегрирование тригонометрических и гиперболических функций. Тригонометрические и гиперболические подстановки
Литература: [1, 2, 9 ,17]
Замечания преподавателя
-
Найти интегралы, выполнив тождественные преобразования, используя линейность операции интегрирования
-
Найти интегралы, пользуясь подведением производной под знак дифференциала
:
-
Найти интегралы, разбивая правильные дроби на сумму простейших дробей или выделяя целую часть и остаток для неправильных дробей
-
Найти интегралы при помощи замены с выделением полного квадрата (можно использовать формулы
,
):
-
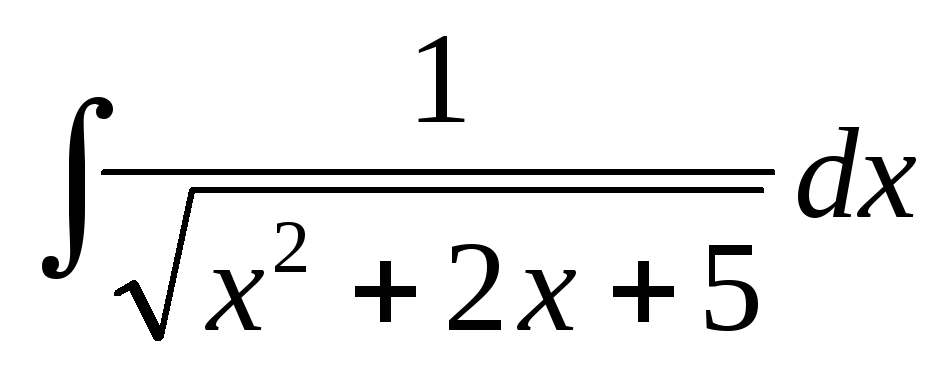
Найти интегралы, преобразуя подынтегральные функции с использованием степенных подстановок
-
Найти интегралы, используя формулу интегрирования произведения
( интегрирование
по частям)
7.
Найти интегралы, комбинируя рассмотренные
выше элементарные приемы:
8.
Проинтегрировать
дробно-рациональные дроби:
, 
-
Проинтегрировать тригонометрические функции:
-
Проинтегрировать гиперболические функции:
-
Найти интегралы, избавляясь от квадратных корней при помощи тригонометрических или гиперболических подстановок:
-
Найти интегралы, комбинируя различные приемы:
Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет»
Направление подготовки 140400.62
«Электроэнергетика и электротехника»
Математика
Самостоятельная работа
РГР № 4 (0,278 ЗЕ)
Применение определенного интеграла к решению задач геометрии и физики
Срок выполнения 5-8 недели
Выполнил студент группы ЭА- 111
Петров А.В.
Работу принял
Кемерово 2011