Министерство образования и науки РФ
Государственное образовательное учреждение
высшего профессионального образования
«Кузбасский государственный технический университет»
Направление подготовки 140400.62
«Электроэнергетика и электротехника»
Математика
Аудиторные практические занятия
1 Семестр
26 занятий (1,411 ЗЕ = 0,332+0,332+0,332+0,415)
Кемерово 2011
Занятия 1-2. Функции. Предел. Непрерывность.
-
Раскрыть простейшие неопределенности:
а)
Неопределенность
,
,
,
,
,
,
б)
Неопределенность
,
в)
Неопределенность
. Раскрыть с использованием эквивалентных
бесконечно малых
,
,
,
,
г)
Неопределенность
(Второй замечательный предел).
,
,
,
-
По формулам функций, схематически построить их графики. В точках разрыва вычислить односторонние пределы и указать их характер.
,
,
.
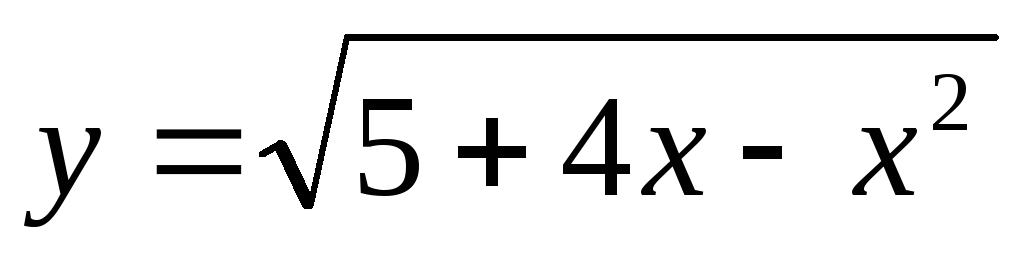
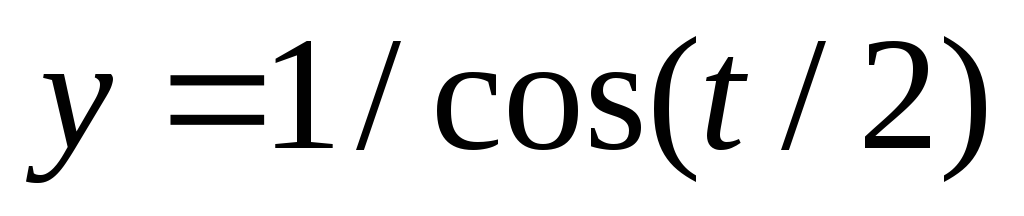
Занятия 3-4. Таблица производных. Производная сложной функции
1.Вычислить производные, используя линейность операции дифференцирования и правила дифференцирования произведения и частного:
2.Вычислить производные, используя правило дифференцирования сложной функции (выписывать цепочку промежуточных переменных):
Справочные материалы
Таблица простейших производных и интегралов
-
, 
. -
, 
. -
, 
.
-
, 
. -
,
. -
, 
. -
, 
. -
, 
,
. -
, 
,
. -
, 
. -
, 
. -
, 
. -
, 
. -
, 
.
,
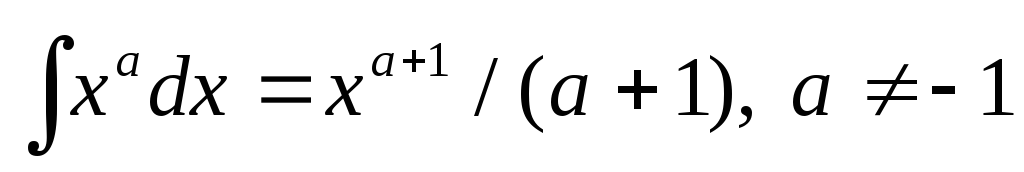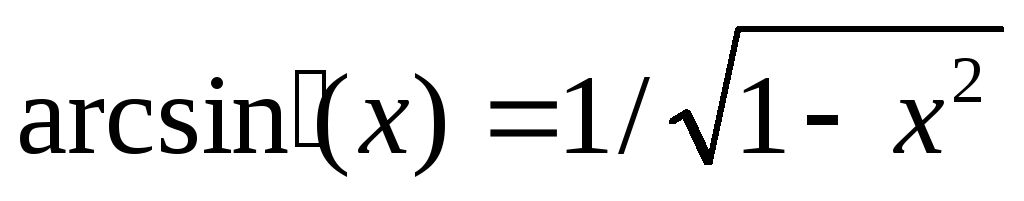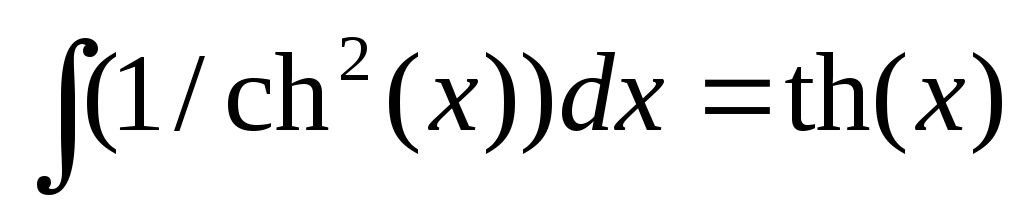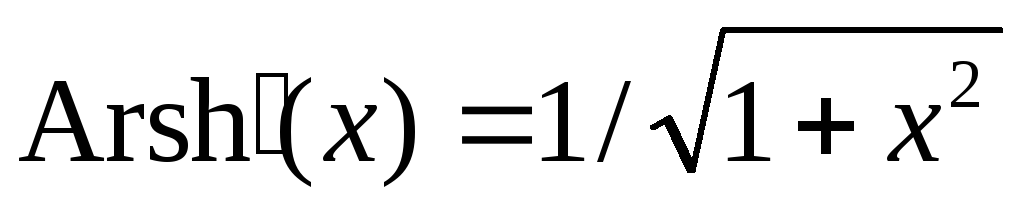Занятия 5-7. Таблица интегралов. Основные методы интегрирования
-
Найти интегралы, используя линейность операции интегрирования:
-
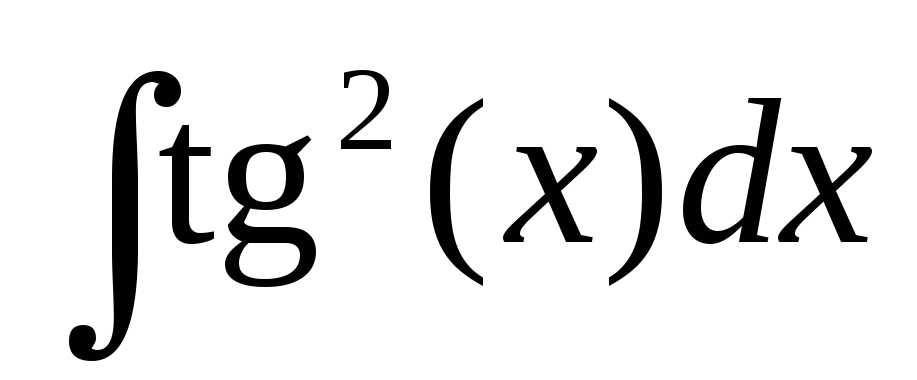
Найти интегралы, пользуясь подведением производной под знак дифференциала
:
-
Найти интегралы, разбивая правильные дроби на сумму простейших дробей или выделяя целую часть и остаток для неправильных дробей:
-
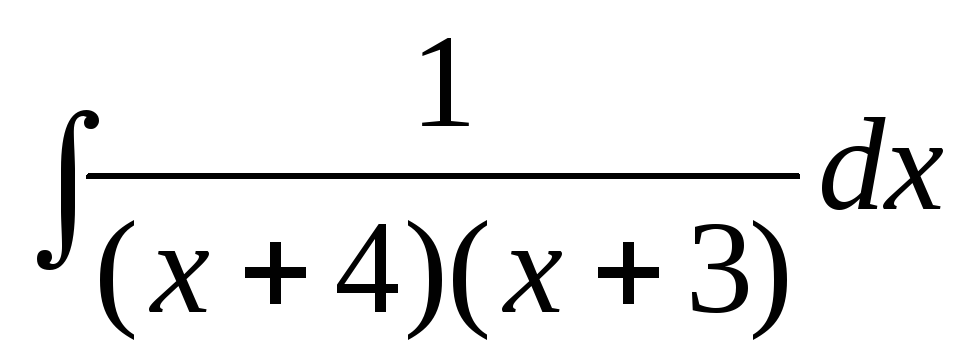
Найти интегралы при помощи замены с выделением полного квадрата (можно использовать формулы
,
):
-
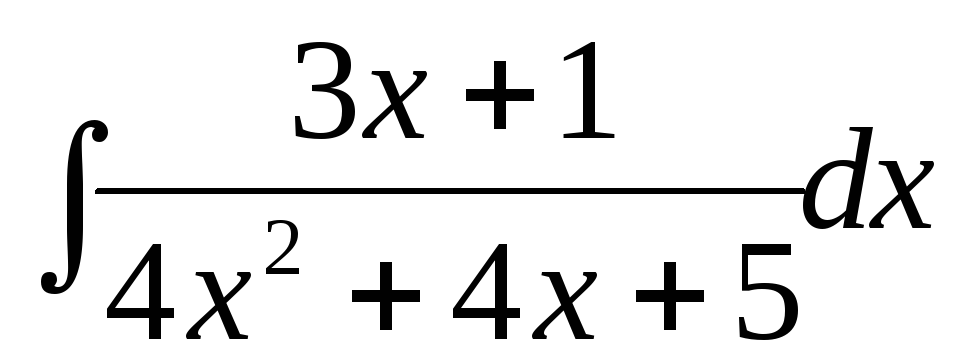
Найти интегралы, преобразуя подынтегральные функции указанными заменами переменных:
-
Найти интегралы, используя формулу интегрирования произведения (интегрирование по частям)
:
-
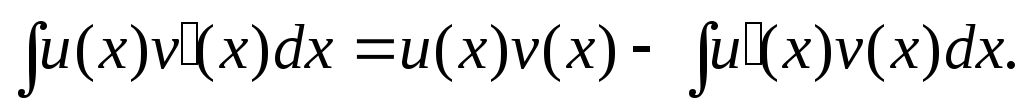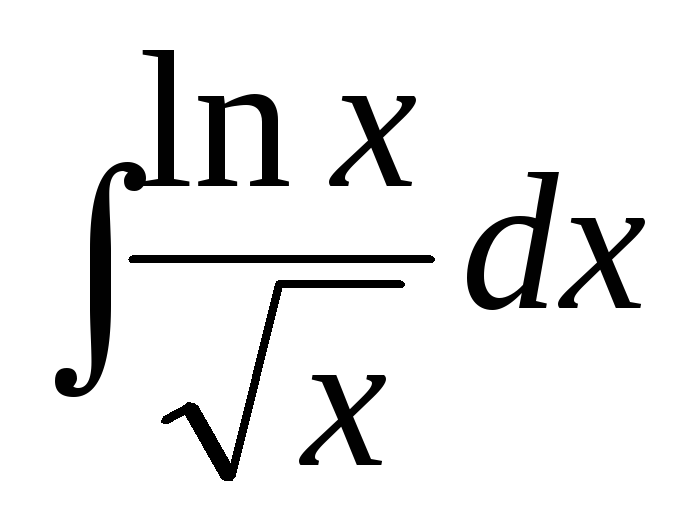
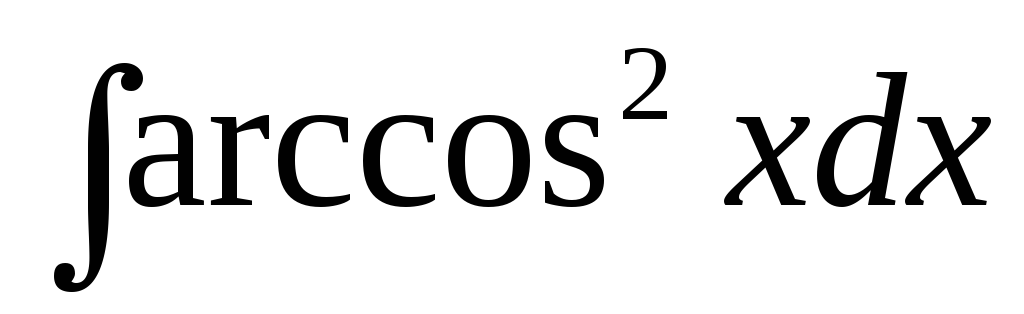
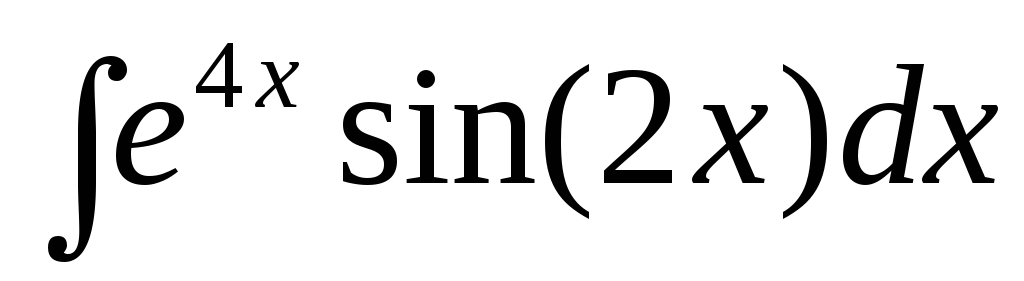
Найти интегралы, комбинируя рассмотренные выше элементарные приемы:
-
Проинтегрировать рациональные дроби:
,
-
Проинтегрировать тригонометрические функции:
-
Проинтегрировать гиперболические функции:
-
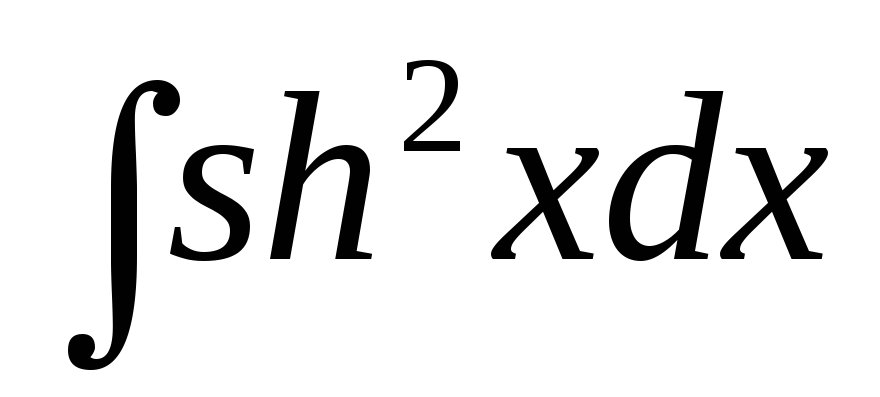
Найти интегралы, избавляясь от квадратных корней при помощи тригонометрических или гиперболических подстановок:
-
Найти интегралы, избавляясь от радикалов при помощи степенных подстановок:
-
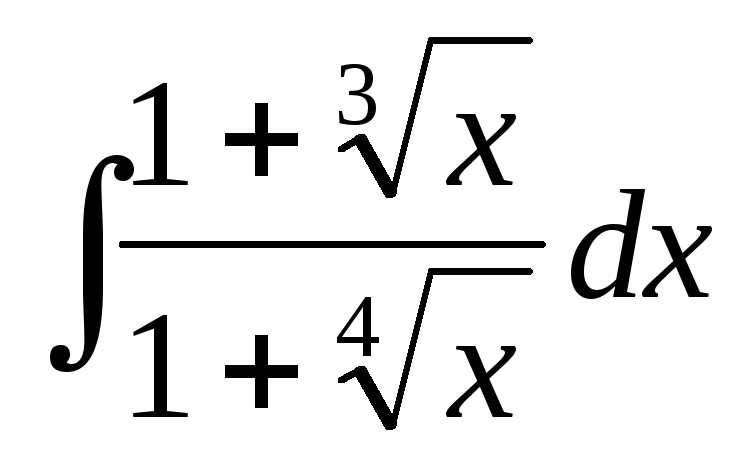
Найти интегралы, комбинируя различные приемы:
Занятие 8. Определенный интеграл. Свойства. Формула Ньютона-Лейбница
1. Вычислить определенные интегралы, используя формулу Ньютона-Лейбница
,
,
,
-
Вычислить, используя свойства определенного интеграла
,
,
Занятие 9. Несобственные интегралы. Вычисление. Признак сравнения.
1.Вычислить несобственные интегралы или исследовать их на сходимость
,
,
,
,
,
Занятия 10. Контрольная работа «Техника дифференцирования и интегрирования»
Занятие 11. Числовой ряд. Сумма ряда. Ряд из членов геометрической прогрессии. Признаки сходимости
1.
Найдите сумму ряда:
,
,
,
Ответы: -1/3, 1, 11/18, 11/12.
2.
Исследуйте на сходимость числовые
ряды:
,
,
,
,
,
,
,
,
,
Занятие 12. Функциональный степенной ряд. Область сходимости
1. Для функциональных рядов найдите область сходимости, радиус сходимости, исследуйте поведение ряда на границах области сходимости:
,
,
,
,
-
Найдите суммы рядов и укажите область сходимости:
,
,
,
,
,
Занятие 13. Ряд Маклорена. РядТейлора. Разложение в ряд. Применение к вычислению пределов и исследованию функций.
-
Используя таблицу разложений функций в ряд Маклорена , разложить функцию в ряд с заданной точностью
.
Для бесконечно малых указать степенной
порядок малости:
-
Разложить функцию по формуле Тейлора вблизи указанной точки
с требуемой точностью
:
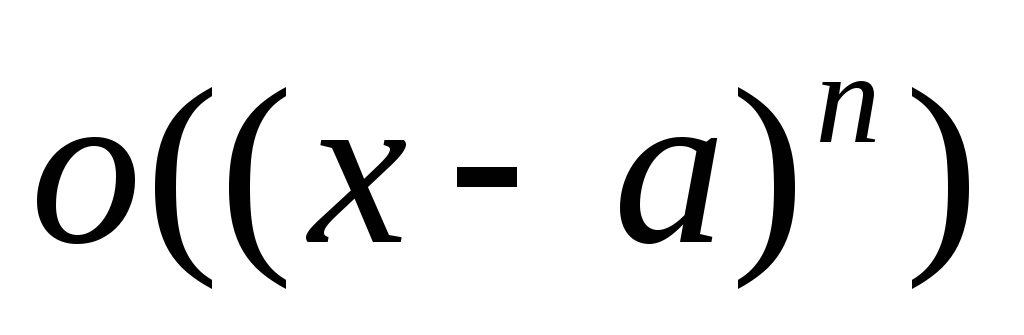3.
Написать приближенные формулы, описывающие
поведение функции при больших значениях
переменной (асимптоты графиков функций
):
-
Написать приближенные формулы, описывающие поведение функции в окрестности ее нулей и точек разрыва:
-
Раскрыть неопределенности:
,
,
,
-
Написать формулы для приближенного вычисления интегралов при помощи разложения подынтегральной функции в степенной ряд. Указать область сходимости.
,
