3.3. Пример №3. Система управления смесителем воды.

Ввод команды shower в окне Command Window пакета Matlab приводит к появлению в окне Simulink структурной схемы нечеткой системы управления смесителем холодной и горячей воды.

С работой смесителя холодной и горячей воды мы сталкиваемся чуть ли не ежедневно. Если напор воды постоянен, то особой необходимости в управлении этим простым устройством нет – достаточно ручку смешения установить в нужное положение и проконтролировать рукой температуру воды. Но, если напор воды постоянно меняется, то без автоматического регулятора температуры не обойтись. В демонстрационном примере рассматривается замкнутая система регулирования температуры с использованием нечеткой логики. Simulink-диаграммы системы приведены на рис. 10.

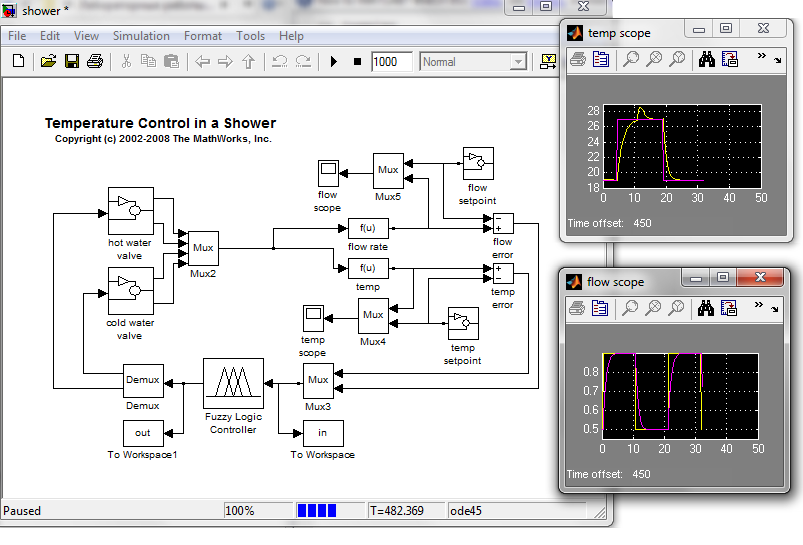
Рис. 10. Simulink-диаграммы системы управления смесителем воды

В системе предусмотрен контроль температуры воды как при ручном управлении, так и в условиях изменения давления горячей и холодной воды после заданной ручной установки. Диаграммы потока и температуры контролируются виртуальными осциллографами.

3.4. Пример №4. Система управления перевернутым маятником.

Ввод команды slcp1 в окне Command Window пакета Matlab приводит к появлению в окне Simulink структурной схемы нечеткой системы управления перевернутым маятником (рис. 11).

Запуск моделирования приводит к появлению анимационной картинки (рис. 12) иллюстрирующей, как представленная система, вырабатывая управляющие воздействия.

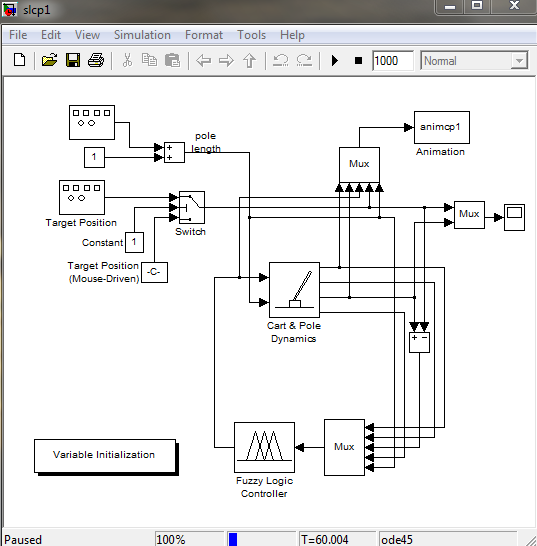
Рис. 11. Структурная схема нечеткой системы управления.

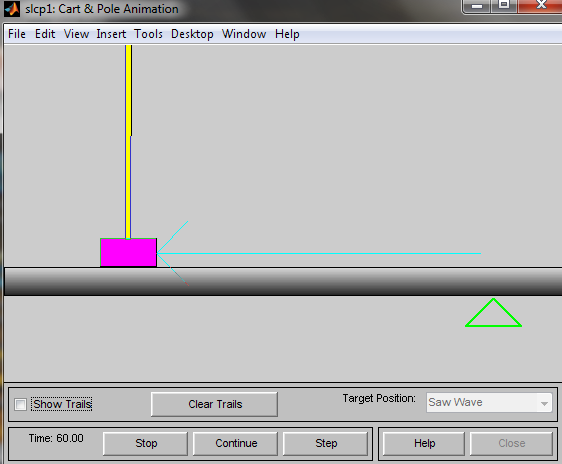
Рис. 12. Динамическая система «перевернутый маятник»

3.5. Пример №5. Система управления двумя перевернутыми маятниками.

Ввод команды slcpp1 в окне Command Window пакета Matlab приводит к появлению в окне Simulink структурной схемы нечеткой системы управления двумя перевернутыми маятниками (рис. 13).

Запуск моделирования приводит к появлению анимационной картинки (рис. 13) иллюстрирующей, как представленная система, вырабатывая управляющие воздействия.

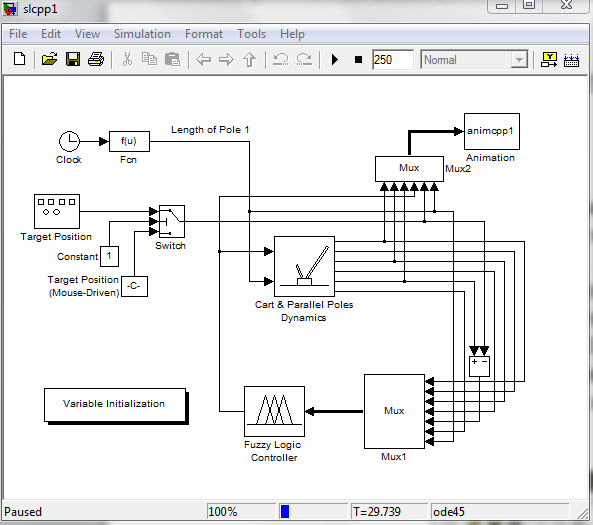
Рис. 13. Структурная схема нечеткой системы управления.

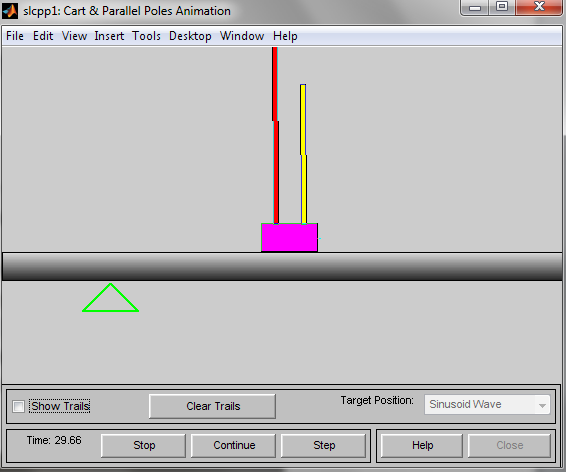
Рис. 14. Динамическая система «перевернутые маятники»

4. Индивидуальные задания

1. Необходимо изучить методы построения нечетких контроллеров средствами нечеткой логики и блоков моделирования Simulink.

2. Промоделировать в Simulink все пять нечетких контроллеров, которые управляют различными динамическими процессами.

3. Получить и привести в отчете словесное описание и графическое отображение правил нечеткого вывода рассмотренных нечетких регуляторов.

5. Содержание отчета

1. Тема лабораторной работы.

2. Цель лабораторной работы.

3. Индивидуальное задание.

4. Результаты выполнения пунктов 1 – 3 индивидуального задания.

5. Выводы по работе.