3. Метод центра гравитации.

Графическое представление функции ρ(b) в декартовых координатах — это кривая, которая вместе с осью абсцисс X, верхней и нижней границами b ограничивает плоскую область. Абсцисса β центра гравитации такой фигуры берется как желаемый оптимум

b_opt=M/F.

Если ρ(b) определяется только для дискретных значений b (так называемые синглетоны), то вычисление центра гравитации модифицируется следующим образом:

b_opt=M/F.

3. Нечеткие системы управления динамическими процессами

3.1. Пример №1. Моделирование качания шара по качели.

Ввод команды slbb в окне Command Window пакета Matlab приводит к появлению в окне Simulink структурной схемы нечеткой системы управления (рис. 2). Задачей управления в данном случае является поддержание такого состояния перекатывающего на качелях шара, при которых он не мог бы с них скатиться.

Запуск моделирования приводит к появлению анимационной картинки (рис. 3) иллюстрирующей, как представленная система, вырабатывая управляющие воздействия, «подталкивающие» то левую, то правую половину качелей, не дает шарику скатиться с них. Точка толчка отображается вершиной треугольника, перемещаемого вдоль коромысла качелей.

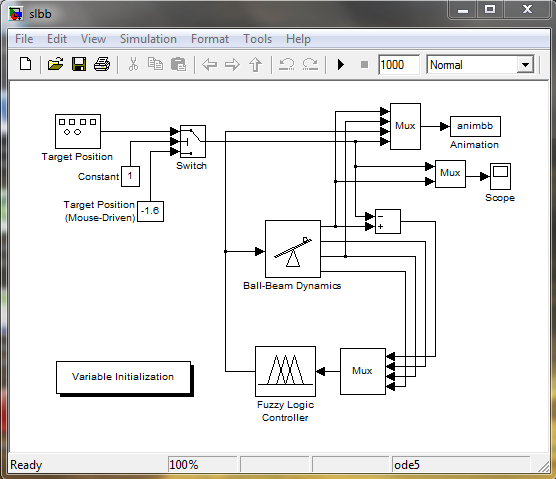
Рис. 2. Структурная схема нечеткой системы управления.

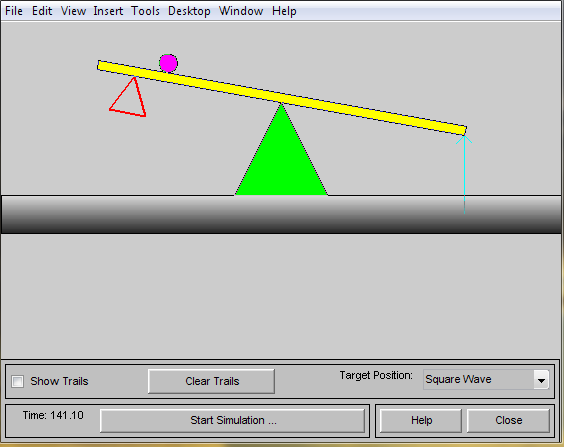
Рис. 3. Динамическая система «шар на качели».

При желании пользователь может просмотреть основные сигналы системы (рис. 4).

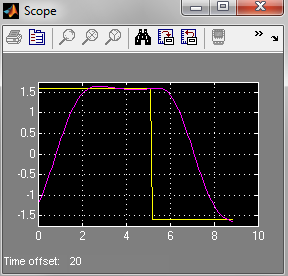
Рис. 4. Основные сигналы системы.

Двойной щелчок мышью на блоке диаграммы модели позволяет вывести окно с параметрами соответствующего блока. Так, на рис. 5 показано такое окно для блока нечеткой логики. Нетрудно заметить, что он характеризуется единственным параметром – именем файла, задающим структуру блока.

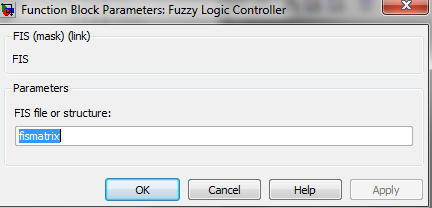
Рис. 5. Окно блока нечеткой логики.

Список Target Position (рис. 3) позволяет выбрать одно из четырех видов воздействий:

• Sinusoid Wave – синусоидальная волна;

• Square Wave – прямоугольная волна;

• Saw Wave – треугольная волна;

• Mouse-Driver – воздействие, задаваемое мышью.

Опция Show Trails, позволяющая накапливать изменения положения шара, коромысла качелей и точки воздействия на них. Благодаря этому можно получить более четкое представление о динамике работы анализируемой системы (рис. 6).

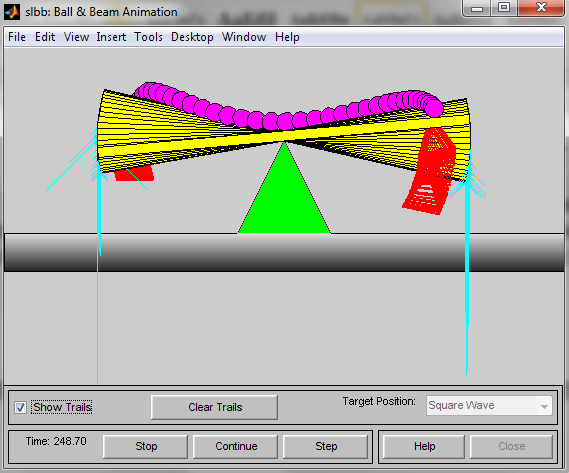
Рис. 6. Иллюстрация управляемого объекта в режиме накопления.

3.2. Пример №2. Моделирование отскоков шара от качелей.

Похожий на описанный выше пример с названием juggler имитирует более сложное движение шара (рис. 7). Здесь шар отскакивает от коромысла качелей, которые перемещаются в точку падения шара. При этом исходное положение коромысла меняется таким образом, чтобы шар при возможности отскакивал вертикально вверх. Выброс шара за пределы области перемещения качелей исключается – учетом отскоков от левой или правой стенок.

В этом примере особенно ценной является возможность моделирования в двух режимах отскока шарика от коромысла качелей – с использованием нечеткой логики и обычной жесткой логики. Последний случай представлен на рис. 8. Нетрудно заметить, что в этом случае вообще не удается добиться отскока шарика строго вертикально вверх – действует правило «угол отражения равен углу падения».

Наряду с окном модели, в этом примере выводится окно контроля Rule Viewer, показанное на рис. 9. Оно позволяет уточнить параметры отскоков шарика.

Данный пример реализован без применения Simulink. МАТLAВ-коды реализующей его программы можно просмотреть, активизировав мышью гиперссылку View code for juggler в окне демонстрации этого примера. Программа занимает немного больше 700 строк и просматривается в редакторе программ системы МАТLAВ.

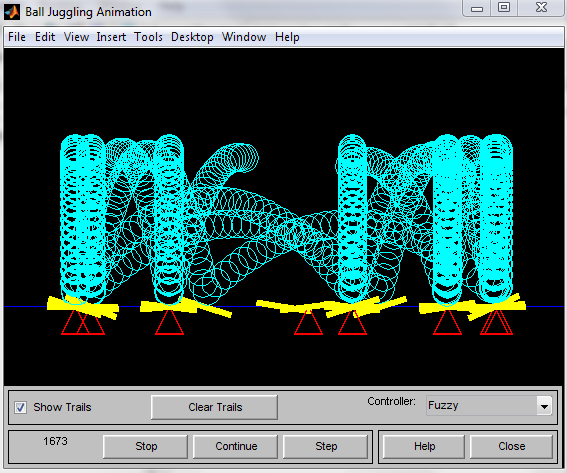
Рис. 7. Динамика отскоков шара при использовании нечеткой логики

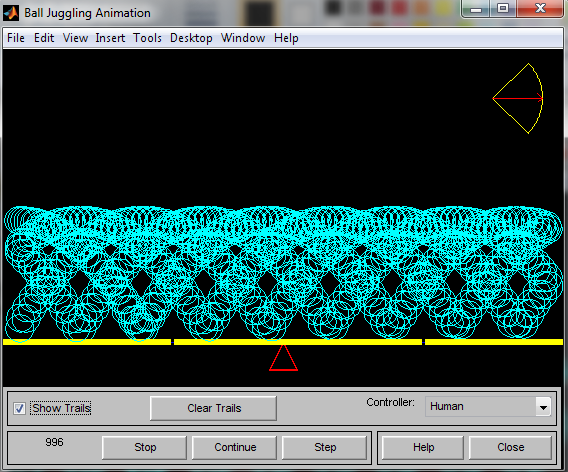
Рис. 8. Динамика отскоков шара при использовании обычной жесткой логики

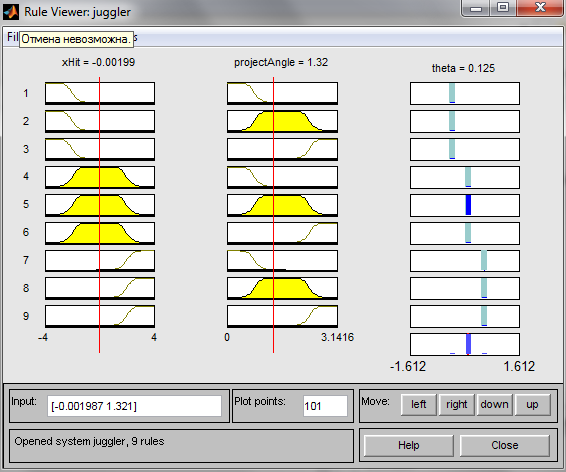
Рис. 9. Окно контроля Rule Viewer