5.4. Непрерывность основных элементарных функций

Теорема. Каждая элементарная функция непрерывна в области своего определения.

1. Многочлен непрерывен на всей числовой оси.

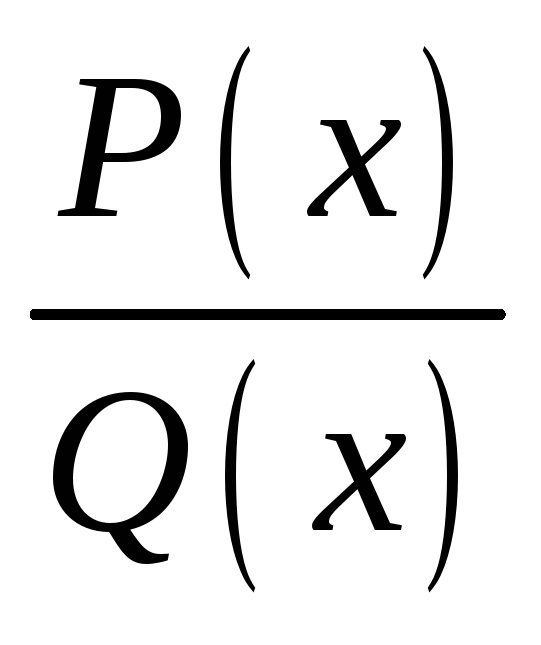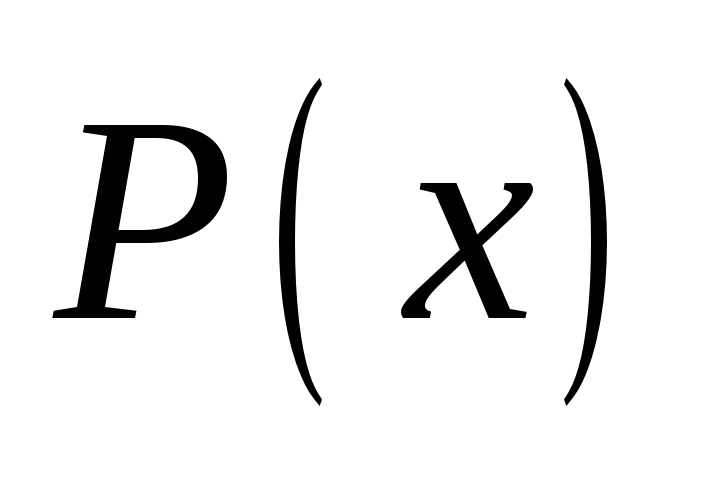2. Рациональная функция , где и 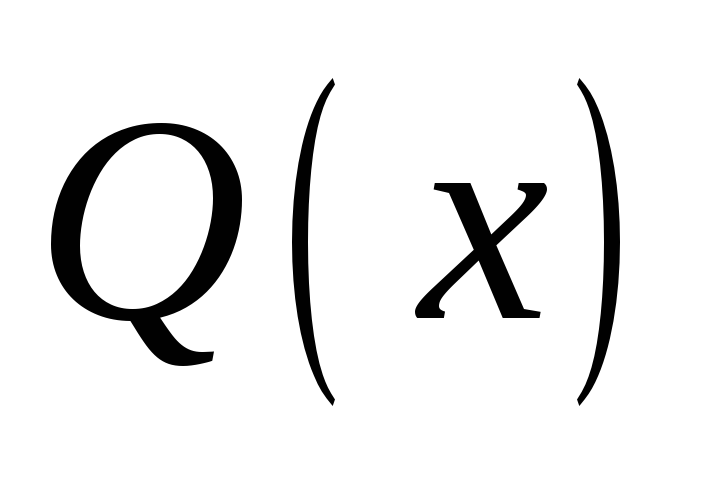– многочлены, непрерывна во всех точках числовой оси, в которых .

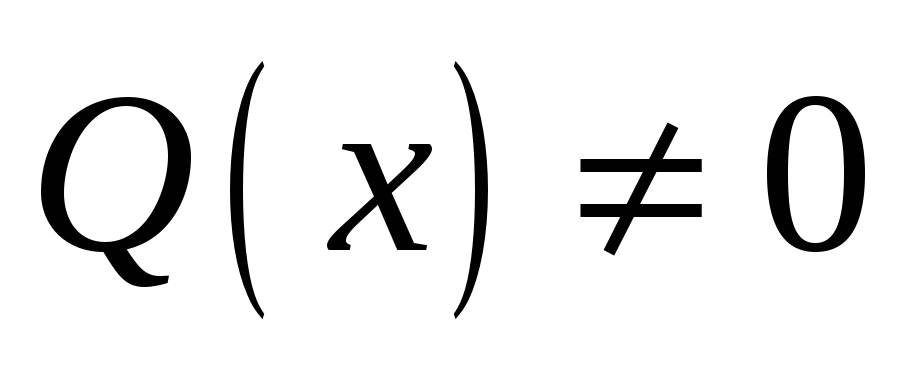3. Показательная функция (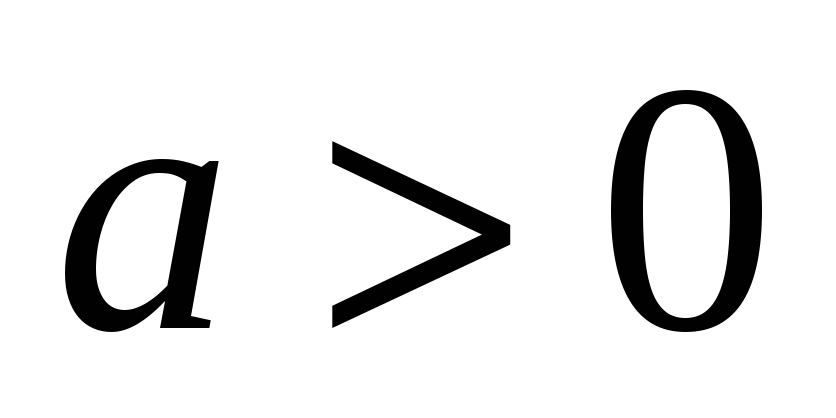) непрерывна на всей числовой оси.

4. Логарифмическая функция 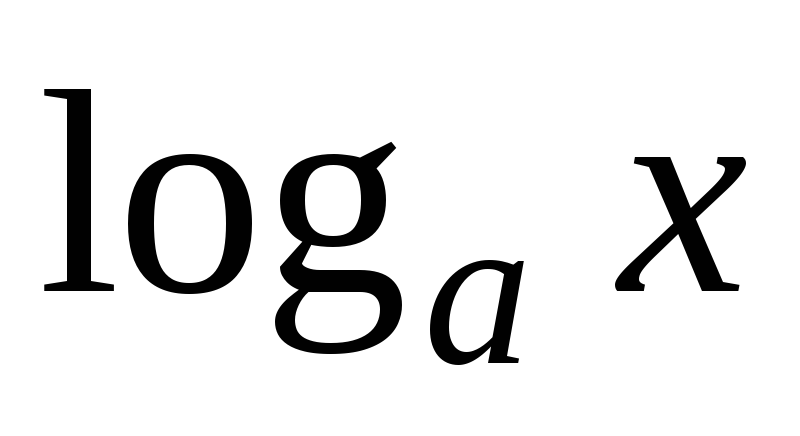(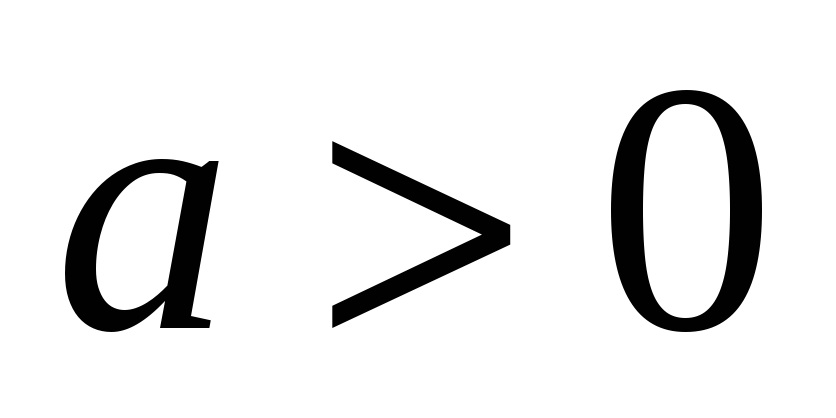, 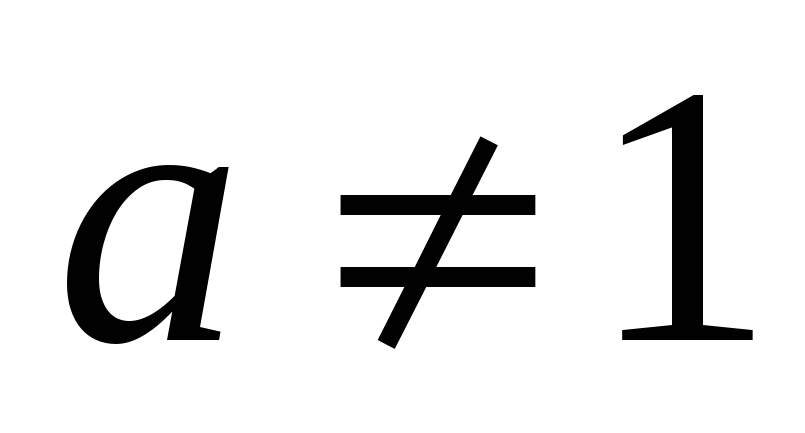) непрерывна при всех .

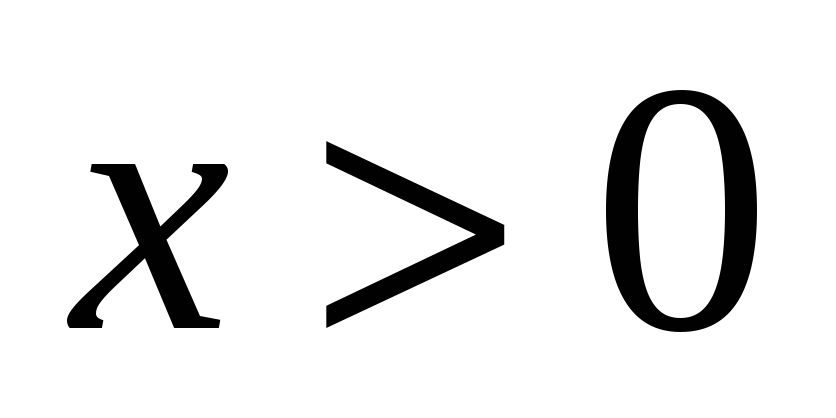5. При любом 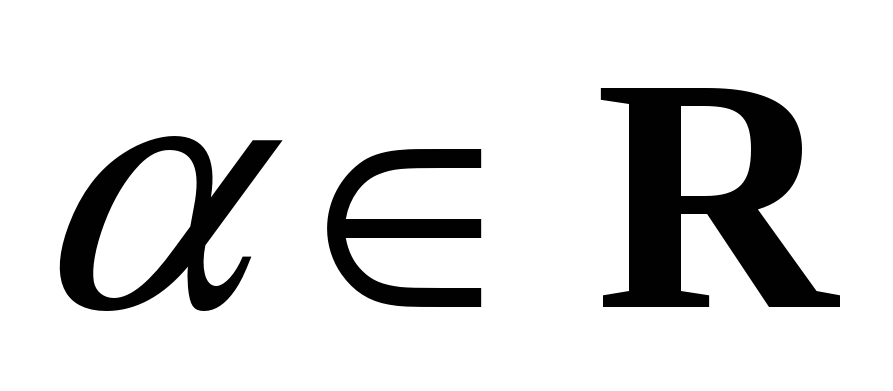степенная функция 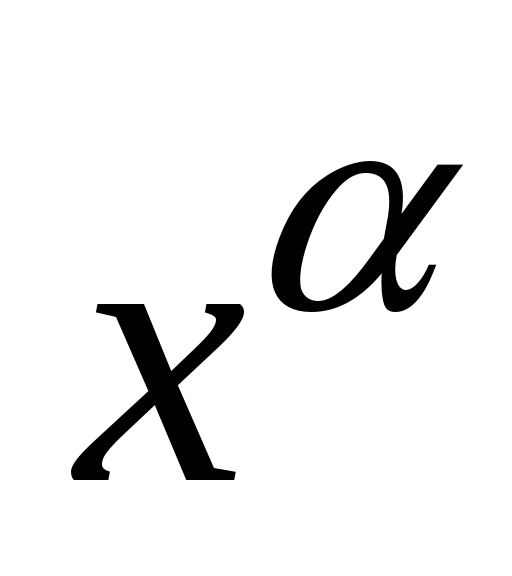непрерывна при всех .

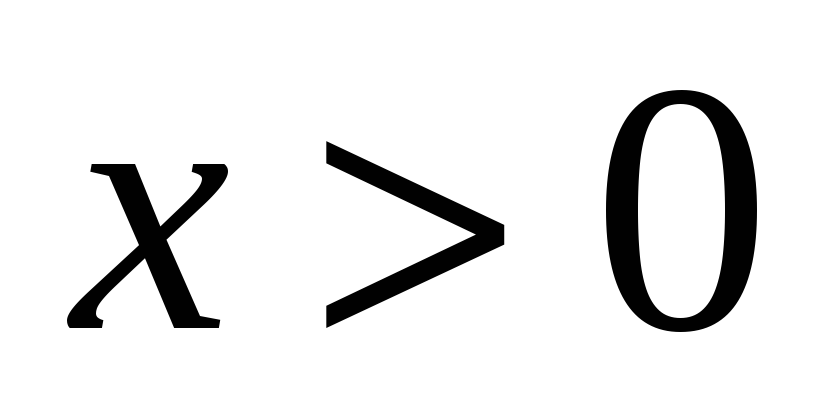6. Функции 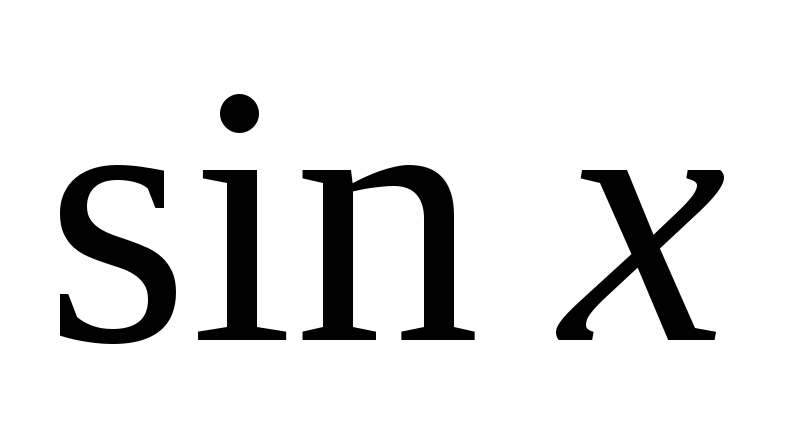и непрерывны на всей числовой оси.

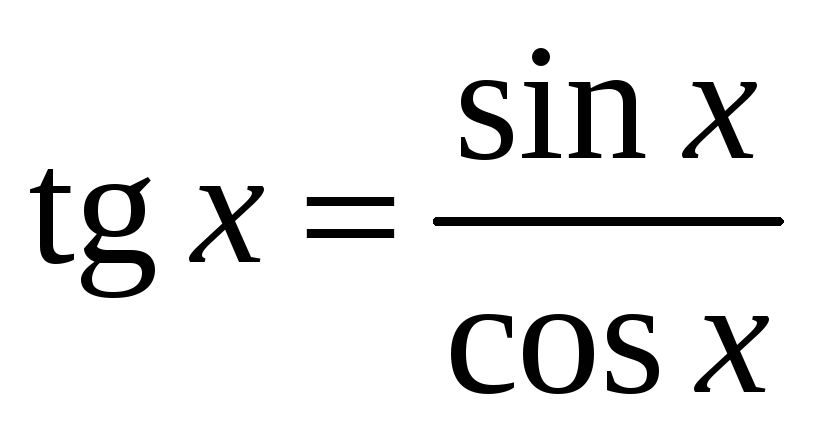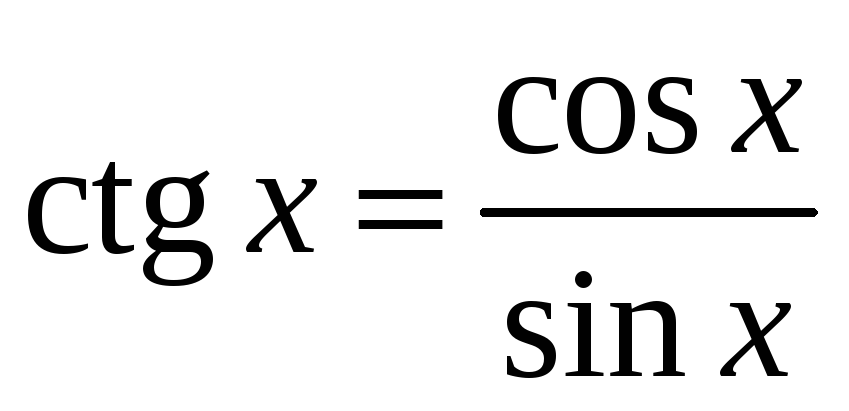7. Функции и непрерывны во всех точках числовой оси, кроме тех, в которых их знаменатели обращаются в нуль.

8. Каждая из обратных тригонометрических функций , , 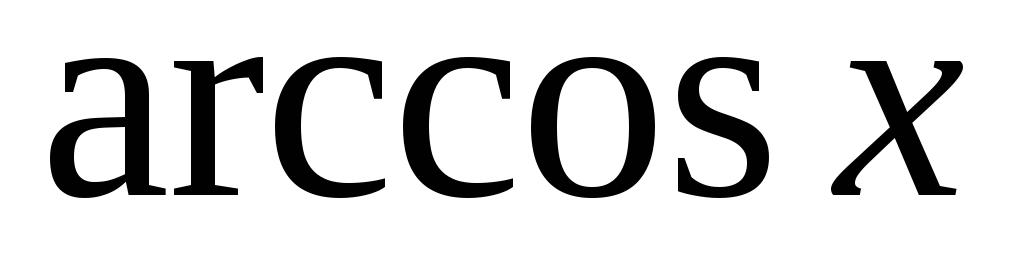, 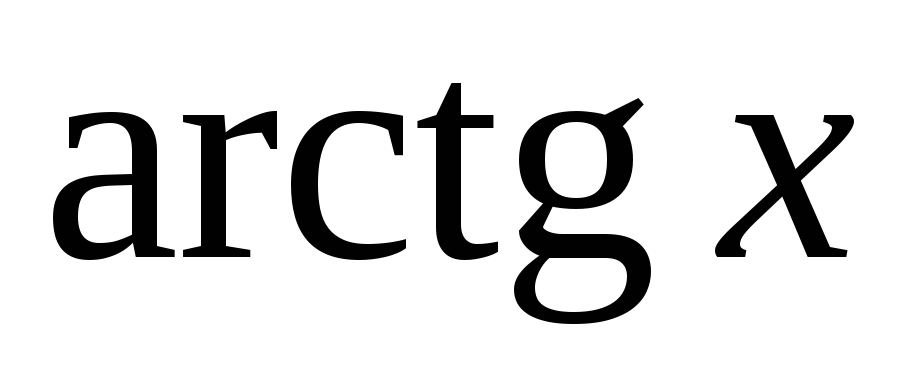непрерывна в области своего определения.

Как известно, элементарной называется такая функция, которую можно задать одной формулой, содержащей конечное число арифметических действий и суперпозиций (операции взятия функции от функции) основных элементарных функций. Поэтому из приведенных выше теорем вытекает: всякая элементарная функция непрерывна в каждой

точке, в которой она определена.

Этот важный результат позволяет, в частности, легко находить пределы элементарных функций в точках, где они определены.

Пример. Найти

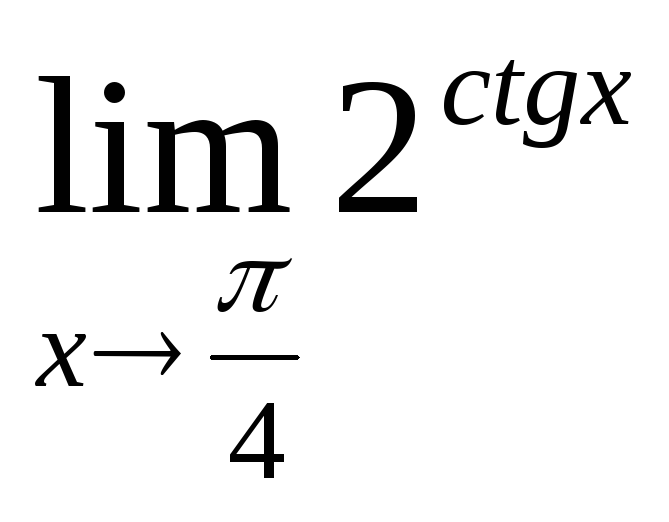
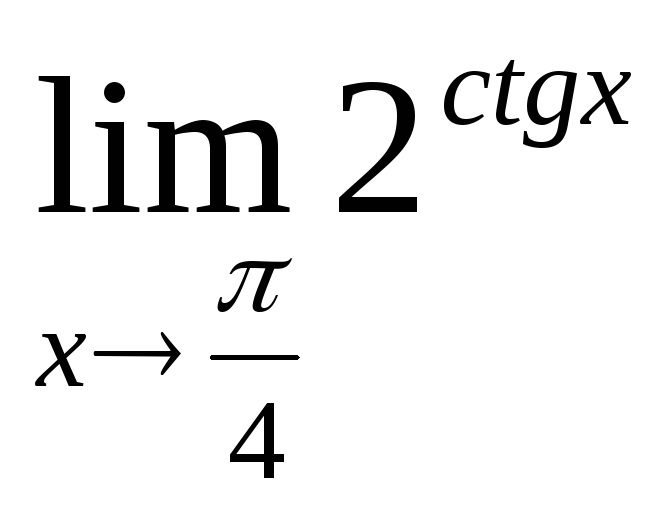Решение: Функция 2^ctgx непрерывна в точке x = , поэтому =2^ctgx =2¹=2

9