
Глава 5
НЕПРЕРЫВНОСТЬ ФУНКЦИИ
ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
5.1. Непрерывность функции в точке.
Односторонняя непрерывность.
Основные теоремы о непрерывных функциях.
Односторонние пределы.
В
определении предела функции
![]() f(x) = А считается, что x
стремится к хо любым
способом: оставаясь меньшим, чем хо
(слева от хо), большим, чем
хо (справа от хо),
или колеблясь около точки xo.
f(x) = А считается, что x
стремится к хо любым
способом: оставаясь меньшим, чем хо
(слева от хо), большим, чем
хо (справа от хо),
или колеблясь около точки xo.
Бывают случаи, когда способ приближения аргумента x к хо существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.
Число А1 называется пределом
функции у = f(x)
слева в точке хо, если
для любого число ε > 0 существует
число δ = δ(ε) > 0 такое,
что при x![]() (xo-δ;
xo),
выполняется неравенство |f(x)-A|<
ε. Предел слева записывают так:
(xo-δ;
xo),
выполняется неравенство |f(x)-A|<
ε. Предел слева записывают так:
![]() f(x)
= А1 или коротко:
f(x)
= А1 или коротко:
f(xo - 0)= А1 (обозначение Дирихле)
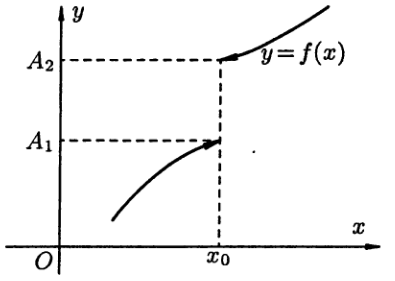
Аналогично определяется предел функции справа, запишем его с помощью символов:
![]()
Коротко предел справа обозначают f(x0+0)=A2.
Пределы функции слева и справа называются
односторонними пределами. Очевидно,
если существует
![]() ,
то существует и оба односторонних
предела, причем A =
A1 = A2.
,
то существует и оба односторонних
предела, причем A =
A1 = A2.
Справедливо и обратное утверждение:
если существуют оба предела f(x0
- 0) и f(x0+0)
и они равны, то существует предел А=![]() и А=f(x0
-0).
и А=f(x0
-0).
Если
же A1![]() A2,
то
A2,
то
![]() не существует.
не существует.
Непрерывность функции в точке
Пусть функция y=f(x) определена в точке x0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке x0 если существует предел функции в этой точке он равен значению функции в этой точке, т.е.
![]() (1)
(1)
Равенство (1) означает выполнение трех условий:
-
функция f(x) определена в точке x0 и в ее окрестности;
-
функция f(x) имеет предел при x → a;
-
предел функции в точке x0 равен значению функции в этой точке, т.е. выполняется равенство (1)
Так
как
![]() то равенство (1) можно записать в виде
то равенство (1) можно записать в виде
![]()
Это означает, что при нахождении предела непрерывной функции f(x) можно
перейти к пределу под знаком функции, то есть в функцию f(x) вместо аргумента x подставить его предельное значение x0.
Определение
1. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если она определена в точке
,
если она определена в точке
![]() и ее окрестности и
и ее окрестности и
![]() .
Это равенство можно переписать в
следующем виде
.
Это равенство можно переписать в
следующем виде
![]() .
Это означает, что под знаком непрерывной
функции можно переходить к пределу.
.
Это означает, что под знаком непрерывной
функции можно переходить к пределу.
Пример
1. Докажем, что функция
![]() непрерывна в любой точке
непрерывна в любой точке
![]() .
.
Решение.
Так как
![]() ,
то функция
,
то функция
![]() непрерывна в точке
непрерывна в точке
![]() .
.
Определение
2. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если для любого
,
если для любого
![]() существует такое
существует такое
![]() ,
что для всех
,
что для всех
![]() ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
![]() ,
выполняется неравенство
,
выполняется неравенство
![]() .
.
Пример
2. Докажем, что функция
![]() непрерывна в любой точке
непрерывна в любой точке
![]() .
.
Решение.
Известно, что для любого
![]() выполняется неравенство
выполняется неравенство
![]() .
Возьмем теперь произвольное
.
Возьмем теперь произвольное
![]() .
Нам надо найти такое
.
Нам надо найти такое
![]() ,
чтобы из неравенства
,
чтобы из неравенства
![]() следовало неравенство
следовало неравенство
![]() .
Но
.
Но
![]() .
Так как
.
Так как
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
Значит, если выбрать
.
Значит, если выбрать
![]() ,
то из
,
то из
![]() следует, что
следует, что
![]() .
Но это и означает непрерывность функции
.
Но это и означает непрерывность функции
![]() в точке
в точке
![]() .
.
Определение
3. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если для любой окрестности
,
если для любой окрестности
![]() точки
точки
![]() существует окрестность
существует окрестность
![]() точки
точки
![]() такая, что
такая, что
![]() для всех
для всех
![]() .
.
Определение
4. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если для любой последовательности
,
если для любой последовательности
![]() значений аргумента, сходящейся к
значений аргумента, сходящейся к
![]() ,
последовательность соответствующих
значений функции
,
последовательность соответствующих
значений функции
![]() сходится к значению
сходится к значению
![]() .
.
Приращением
аргумента в точке
![]() называется разность
называется разность
![]() ,
разность
,
разность
![]() называется приращением
функции.
называется приращением
функции.
Пусть функция
![]() определена в некотором интервале
определена в некотором интервале
![]() (рис.4). Возьмем произвольную точку
(рис.4). Возьмем произвольную точку
![]() .
Для любого
.
Для любого
![]() разность
разность
![]() называется приращением аргумента
называется приращением аргумента
![]() в точке
в точке
![]() и обозначается
и обозначается
![]() .
Отсюда
.
Отсюда
![]() .Разность
значений функции
.Разность
значений функции
![]() называется приращением функции
f(x) в точке
называется приращением функции
f(x) в точке
![]() и обозначается
и обозначается
![]() или
или
![]() .
.

Определение
5. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() ,
если бесконечно малому приращению
,
если бесконечно малому приращению
![]() аргумента в точке
аргумента в точке
![]() соответствует бесконечно малое приращение
функции
соответствует бесконечно малое приращение
функции
![]() ,
т. е.
,
т. е.
![]() .
.
Покажем, что это определение эквивалентно первому определению непрерывности функции. Для этого рассмотрим детальнее предыдущее определение.
![]() .
.
Воспользовавшись тем, что предел
постоянной![]() есть сама постоянная, получим
есть сама постоянная, получим
![]() .
.
Тогда функция
![]() ,
определенная в точке
,
определенная в точке
![]() и в некоторой ее окрестности,
называется непрерывной в точке
и в некоторой ее окрестности,
называется непрерывной в точке
![]() ,
если существует предел функции в этой
точке, который равен значению функции
точке
,
если существует предел функции в этой
точке, который равен значению функции
точке
![]() .
Это означает, что при нахождении предела
непрерывной функции достаточно в
выражение функции
.
Это означает, что при нахождении предела
непрерывной функции достаточно в
выражение функции
![]() подставить вместо аргумента
подставить вместо аргумента
Пример
3. Докажем непрерывность
функции
![]() во всех точках
во всех точках
![]() .
.
Решение.
Имеем
![]()
![]() .
Так как
.
Так как
![]() ,
то функция непрерывна.
,
то функция непрерывна.
Определение
6. Функция
![]() называется непрерывной
в точке
называется непрерывной
в точке
![]() справа (слева), если
правый (левый) предел этой функции в
точке
справа (слева), если
правый (левый) предел этой функции в
точке
![]() равен значению функции в этой точке.
Символически это записывается так
равен значению функции в этой точке.
Символически это записывается так
![]() ,
,
![]() .
.
Теорема
1. Для того, чтобы функция
была непрерывна в точке
![]() ,
необходимо и достаточно, чтобы она была
непрерывна в этой точке справа и слева.
В этом случае
,
необходимо и достаточно, чтобы она была
непрерывна в этой точке справа и слева.
В этом случае
![]()
![]() .
.
Приведем также следующие важные свойства функций, непрерывных в точке.
Теорема
2. Если функция
![]() непрерывна в точке
непрерывна в точке
![]() ,
то она ограничена в некоторой окрестности
этой точки.
,
то она ограничена в некоторой окрестности
этой точки.
Теорема
3. Если функция
![]() непрерывна в точке
непрерывна в точке
![]() и
и
![]() (
(![]() ),
то существует окрестность точки
),
то существует окрестность точки
![]() ,
в которой
,
в которой
![]() (
(![]() ).
).
Кратко
эту теорему можно сформулировать так:
функция, непрерывная в точке
![]() ,
в достаточно малой окрестности этой
точки имеет тот же знак, что и
,
в достаточно малой окрестности этой
точки имеет тот же знак, что и
![]() .
.
Обратим
внимание, что из непрерывности функции
в точке
![]() не следует непрерывность этой функции
в достаточно малой окрестности точки
не следует непрерывность этой функции
в достаточно малой окрестности точки
![]() .
Например, функция
.
Например, функция
![]()
непрерывна
в точке
![]() и разрывна во всех точках отличных от
нуля.
и разрывна во всех точках отличных от
нуля.
Определение
7. Функция
![]() называется непрерывной на множестве
называется непрерывной на множестве
![]() ,
если она непрерывна в каждой точке
,
если она непрерывна в каждой точке
![]() .
.
Так,
в примере 1 функция непрерывна на
множестве точек
![]() ,
в примере 2 функция непрерывна на
множестве
,
в примере 2 функция непрерывна на
множестве
![]() ,
в примере 3 функция непрерывна на
множестве точек
,
в примере 3 функция непрерывна на
множестве точек
![]() .
.
