51.4 Линейная независимость собственных векторов, имеющих попарно-различные собственные значения

Покажем, что имеет место следующая теорема:

Теорема 51.6: Если собственные значения линейного оператора попарно различны, то соответствующие им собственные вектора линейно независимы.

Доказательство:

Используем метод математической индукции по числу собственных значений m :

1. База индукции: m=1

Так как собственный вектор x≠0, то система {x} линейно независима (см. §16, теорема 16.0).

2. Шаг индукции:

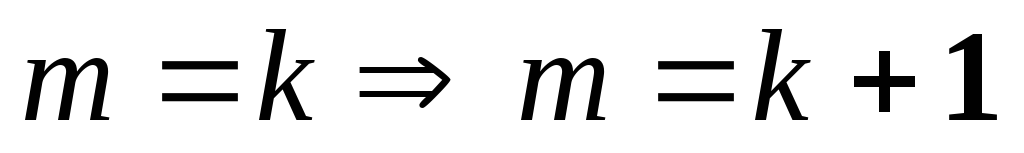
Имеем: вектора линейно независимы (попарно различные собственные значения - ; соответствующие им собственные вектора - ).

Рассмотрим произвольную линейную комбинацию для собственных векторов

(51.7)

Тогда

то есть доказано равенство

(51.8)

Умножая обе части (51.7) на λ_k+1 и вычитая полученное равенство из (51.8), имеем

(51.9)

А так как система линейно независима по индуктивному предположению, то

(51.10)

Ввиду того, что (то есть ) для любых j=1,…k (собственные значения попарно различны), из равенства (51.10) получаем, что

(51.11)

Подставляя вместо в (51.7) их значения из (51.11), получим, что , а так как , то из теоремы 16.0 имеем , то есть (см. (51.11): , и, следовательно, система линейно независима (ибо мы показали, что равенство (51.7) может выполняться только при нулевых значениях ). Теорема 51.6 доказана.

Простым следствием теоремы 51.6 является следующая теорема:

Теорема 51.7: Если все корни характеристического многочлена линейного оператора действительные и простые (попарно различные), то в линейном пространстве имеется базис из собственных векторов линейного оператора .

Рассмотрим матрицу линейного оператора в базисе его собственных векторов:

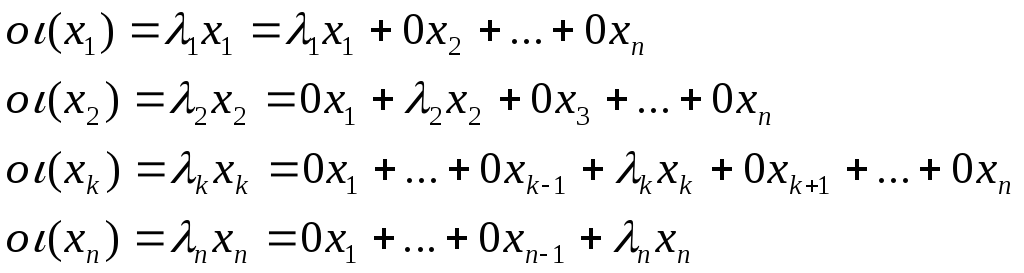
то есть эта матрица имеет вид: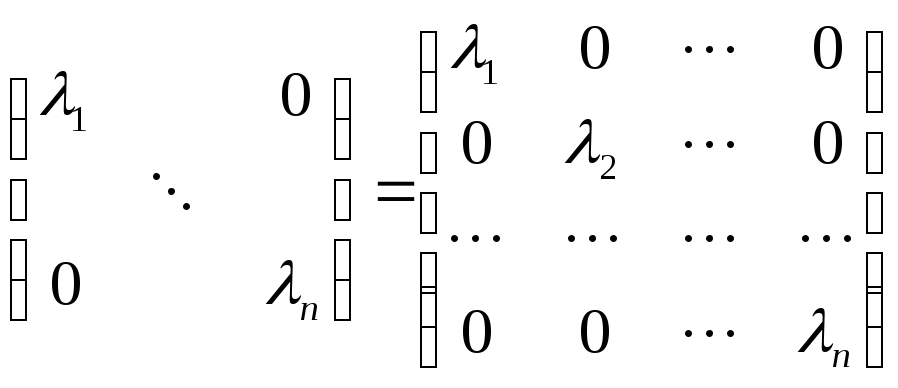

и является диагональной матрицей.

Итак, доказаны следующие две теоремы:

Теорема 51.8: Матрица линейного оператора в базисе его собственных векторов является диагональной.

Теорема 51.9: Если уравнение

(51.12)

Имеет вещественные простые (попарно различные) корни, то существует такая невырожденная матрица C , что C^-1∙A∙C является диагональной матрицей.

Эта матрица C будет матрицей перехода к базису из собственных векторов линейного оператора соответствующих собственным значением , являющихся корнями уравнения (51.12).

§52 Симметричный линейный оператор

52.1 Определение симметричного линейного оператора (СЛО)

Определение: действительный ЛОА симметричен, если для любых x и y элементов и из ЛП верно равенство .

52.2 Ортогональное дополнение и его инвариантность для симметричного линейного оператора

Теорема 52.2: если - СЛО, а - ИПП, то ортогональное дополнение - также ИПП т.е. (определения см. в § 50; п.50.4)

Доказательство:

52.3 Матрица симметричного линейного оператора

в ортогональном базисе

Если имеется СЛО, ОНБ и матрица в этом базисе. Тогда справедлива теорема 52.2: симметричный ЛО имеет ОНБ, состоящий из его собственных векторов и все его собственные значения действительны.

Введем условные обозначения: - собственное значение, а – собственный вектор СЛО

Доказательство:

действительное число

На этом вторая часть теоремы доказана. Перейдем к первой:

Пусть теперь так: λ - собственное значение СЛО, а x≠0 - его собственный вектор. Используем метод мат. индукции (от частного к общему).

1. База: пусть пространство одномерно. В таком случае базис состоит из одного (ненулевого) элемента, каким может быть в принципе собственный вектор χ.

2. Шаг: 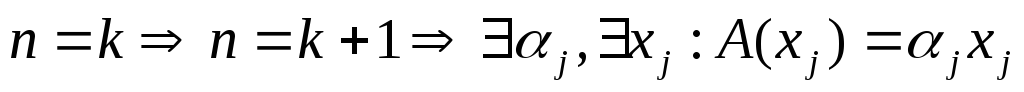j=1,2…,k+1

((k+1) – размерность всех ЛП) -ИПП, значит - ИПП с размерностью (см. п.50.4 в § 50), где (в ) имеется ОНБ: из собственных векторов СЛО со значениями . Тогда - ОНБ во всем линейном пространстве из собственных векторов СЛО с собственными значениями

Отметим, что если - ОНБ из собственных векторов с собственными значениями , то согласно теореме 51.8 (см. п.51.4 в § 51), его матрица в базисе будет - диагональной матрицей.

Итак, доказано следующее:

Теорема 52.3: Любой симметричный ЛО имеет ортонормированный базис, в котором его матрица диагональна.

Если – матрица перехода в базисе собственных векторов симметричного линейного оператора , то так как базис у собственных векторов – ОНБ, то имеет место равенство (см. формулу (50.8) в п.50.3,§ 50).

Определение: матрица называется симметричной, если .

Теорема 52.4: Симметричный ЛО в ОНБ действительного ЛП имеет симметричную матрицу.

Доказательство:

Так как в действительном Евклидовом пространстве:

, тогда (см. формулу 50.1), т.е. из теоремы 53.5 и 53.4 легко следует.

Теорема 52.5: Для всякой симметричной матрицы А существует ортогональная матрица С такая, что матрица является диагональной матрицей. Матрица С является матрицей перехода к базису собственных векторов симметричного линейного оператора , заданного матрица A (т.е.).