50.5 Преобразование матрицы ло при переходе к другому базису

Пусть 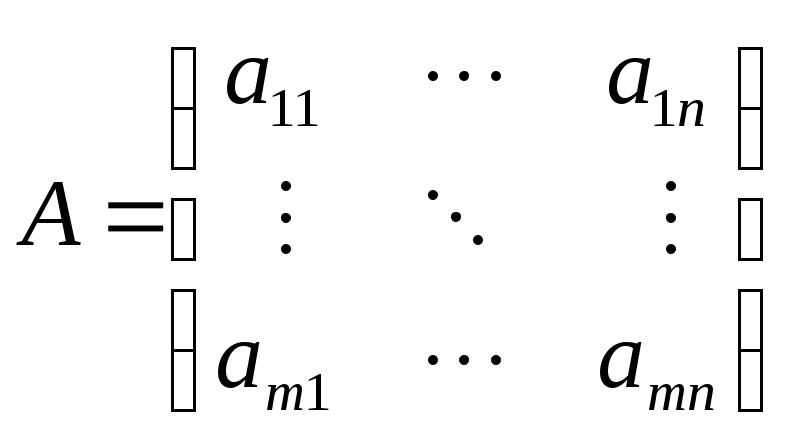- матрица ЛО в базисе , а - матрица перехода от базиса к базису . Найдем матрицу ЛО в базисе . При этом из п.50.2 имеем (50.13)

( - элементы обратные матрицы использующие равенства (50.1) и (50.4)):

, где и

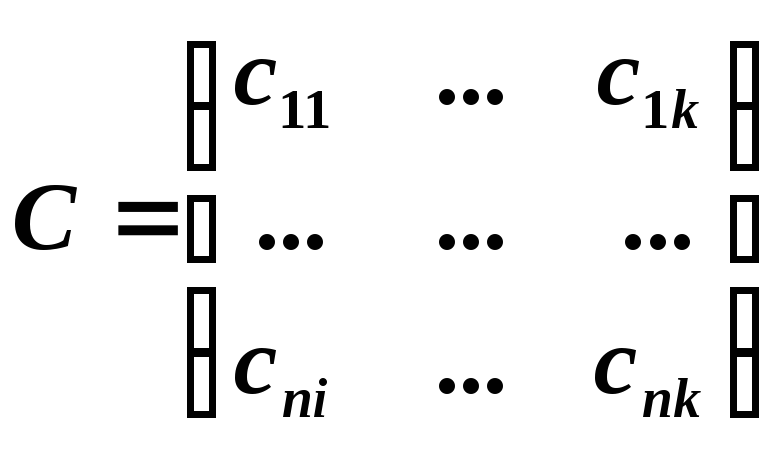
. Таким образом матрица ЛО в базисе появляется 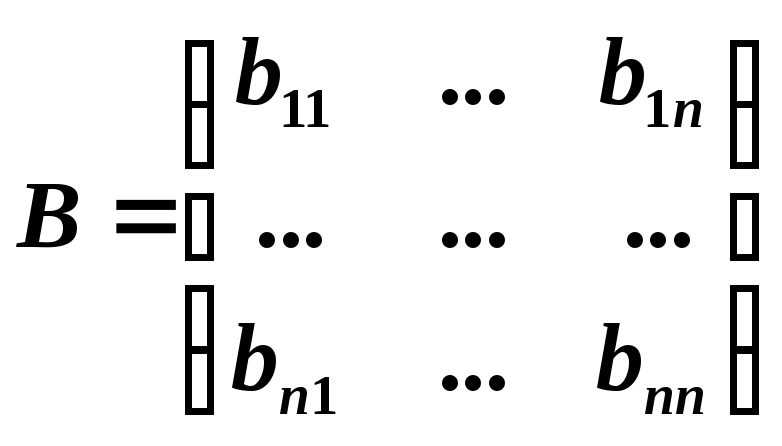причем B=DС, где матрица 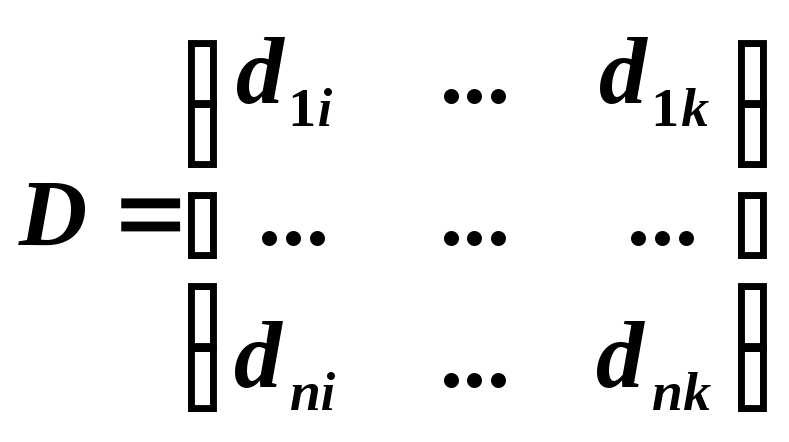; D=C^-1A. Мы показали что справедливо следующая теорема: Матрица линейного оператора в базисе является матрица B=C^-1AC (50.14)

50.6 Характеристический многочлен линейного оператора

и его инвариантность относительно выбора базиса

Пусть имеется ЛО , переводящий ЛП X из самого себя и имеется базис. Тогда рассмотрим уравнение:

(50.15)

Равенство определяет P(λ) - характеристический многочлен ЛО . Этот многочлен не изменится, если изменить базис элементов (он инвариантен относительно выбора базиса):

§51 Собственные вектора и собственные значения линейного оператора

51.1 Определение собственных значений и собственных векторов

Определение: Число λ называется собственным значением линейного оператора , если найдется такой элемент x≠0 из линейного пространства, что

(51.1)

Определение: Элемент линейного пространств x, определённый равенством (51.1), называется собственным вектором линейного оператора , соответствующим собственному значению λ .

51.2 Связь собственных значений с корнями характеристического многочлена

Пусть линейный оператор в некотором базисе имеет матрицу A. Определим, какими должны быть его собственные значения. Для этого уравнение (51.1) перепишем в матричной форме (см. равенство (50.2)), причем за 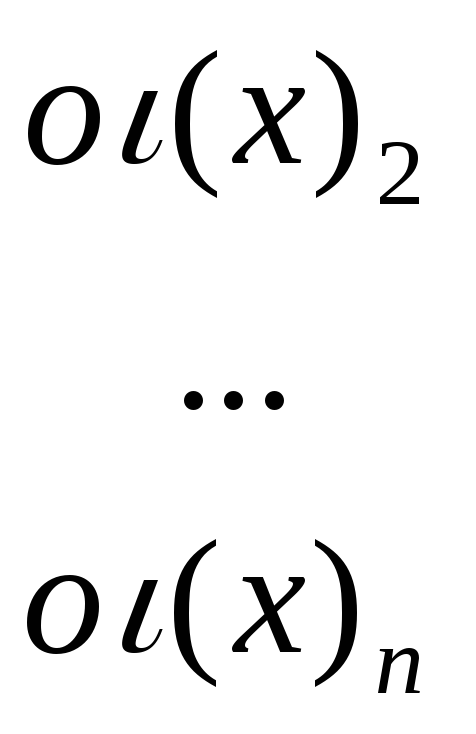обозначим столбец координат элемента в базисе (то есть ):

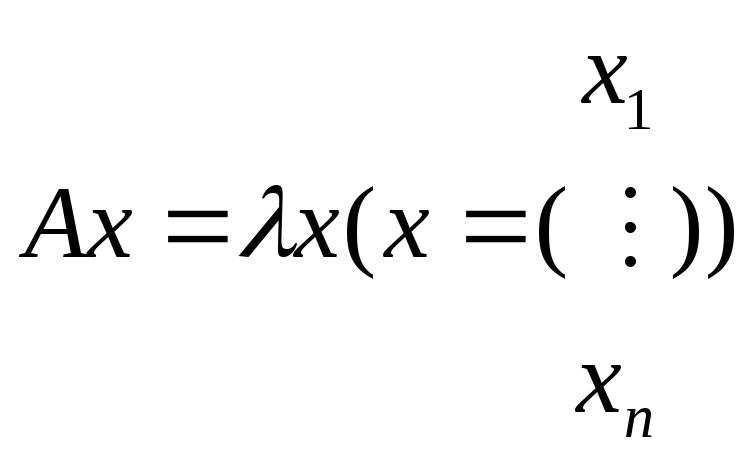, либо или 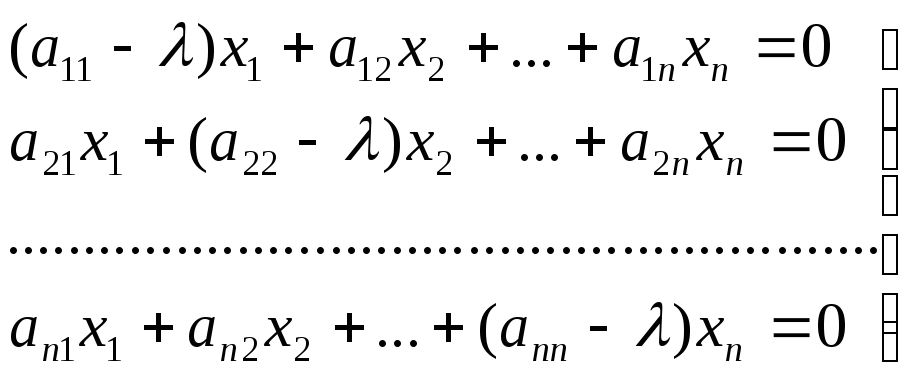(51.2)

Это означает, что система линейных уравнений (51.2) имеет ненулевое решение. А так как также является решением системы (51.2), то отсюда следует, что система (51.2) не определена, и поэтому (см. §7, теорема 7.1)

(51.3)

А уравнение (51.3) означает, что λ является корнем характеристического многочлена линейного оператора (см. п. 50.6 в § 50, равенство (50.15)).

Обратное следует из того, что если , то множество решений системы (51.2) является линейным пространством ненулевой размерности (см. §19, теорема 19.2), и, стало быть, имеет ненулевое решение. Мы показали, что справедливы следующие две теоремы:

Теорема 51.1: Число λ является собственным значением линейного оператора тогда и только тогда, когда оно является корнем его характеристического многочлена.

Теорема 51.2: Все собственные вектора, соответствующие заданному собственному значению λ, образуют линейное подпространство. Ибо столбцы их координат являются решением однородной системы (51.2)

51.3 Существование одномерных и двумерных инвариантных подпространств

Теорема 51.3: Линейная оболочка, натянутая на собственный вектор x, соответствующий собственному значению λ линейного оператора , является инвариантным подпространством линейного оператора .

Доказательство:

Для любого имеем y=αx при некотором α. Тогда , то есть и теорема 51.3 доказана.

А так как степень характеристического многочлена P(x) совпадает с размерностью всего линейного пространства, то имеет место следующая теорема:

Теорема 51.4: Всякий линейный оператор в линейном пространстве нечётной размерности имеет инвариантное одномерное подпространство (являющееся линейной оболочкой собственного вектора x, соответствующее собственному значению λ - вещественному корню характеристического многочлена линейного оператора ).

(- мнимая единица, т.е )

Пусть теперь - комплексный корень характеристического многочлена. Перейдя к матричной форме записи, получим, что система линейных уравнений (51.2) должна иметь комплексное ненулевое решение z=x+y_j, или (A - вещественная матрица, ибо - вещественный линейный оператор):

(51.4)

Раскроем в (51.4) скобки:

Сравнивая вещественные и мнимые части обеих частей последнего равенства, имеем

и (51.5)

или, переходя к линейному оператору и полагая 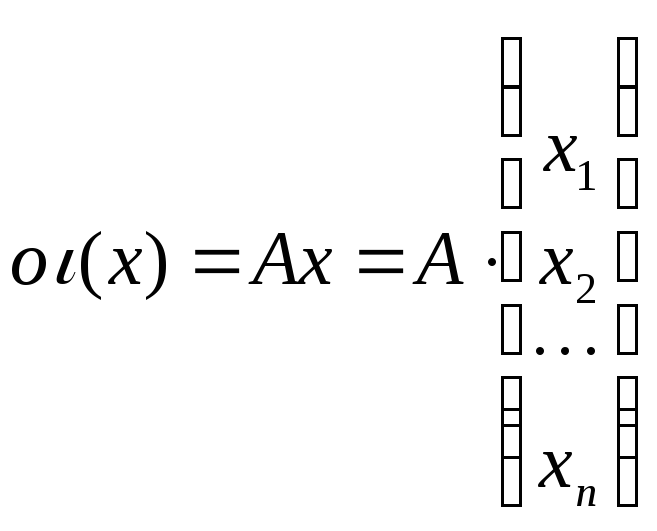(см. (50.2)) ранее выбранный базис, получим:

и (51.6)

Берем теперь любое ,то есть при некоторых α и β. Тогда:

то есть L({x;y} (являющееся двумерным линейным подпространством) – инвариантное подпространство линейного оператора . Таким образом, доказана следующая теорема:

Теорема 51.5: Всякий линейный оператор имеет одномерное или двумерное инвариантное подпространство.