Глава 5. Евклидовы пространства. Линейные операторы

§48 Преобразование координат при повороте оси и квадратичные формы для функций двух переменных

48.1 Преобразование координат при повороте оси на угол α

Для вектора преобразование координат будет следующим (см.§35):

Где - «старые» координаты.

48.2 Квадратичные формы для функции двух переменных

Определение 48.1: квадратичной формой (КФ) для функции двух переменных называется следующее выражение:

Q(x,y) = Ax² + 2Bxy + Cy² (48.1)

Теорема: существует такой поворот осей, при котором в выражении для КФ не будет произведения переменных.

Из §35 имеем (см. п.35.2):

(35.10)

В этом случае 2Bxy = 0.

§49 Евклидовы пространства

49.1 Определение Евклидова пространства (ЕП)

Определение: Линейное пространство является Евклидовым, если в нем задано скалярное произведение величин a и b, обладающее свойствами:

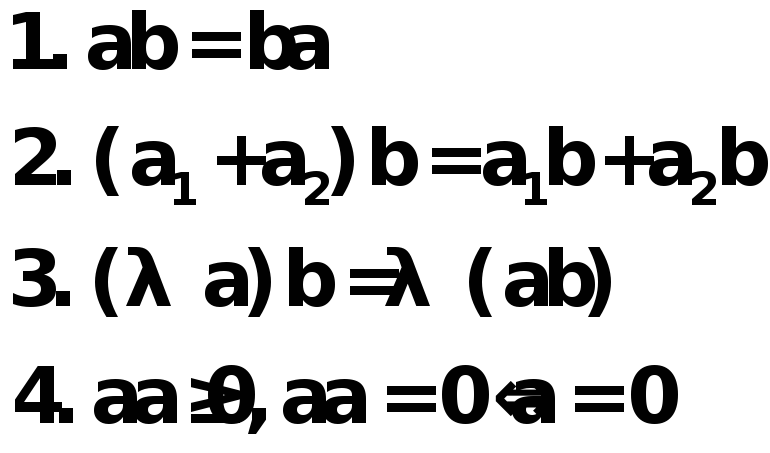
Из свойства 3, (положив λ=0), легко следует, что 0•b=0 )

Нормой называется выражение:

(49.1)

49.2 Неравенство Коши-Буняковского или неравенство Шварца. Неравенство треугольника

Неравенство Коши-Буняковского (или неравенство Шварца) имеет вид:

(42.2)

Доказательство:

при . И тогда дискриминант квадратичной формы должен быть 0. Поэтому

, и

, т.е.

Неравенство Коши-Буняковского (иногда его называют неравенством Шварца) позволяет определить угол между любыми двумя элементами евклидова пространства по формуле:

Неравенство треугольника известно всем со школы, и имеет вид:

(49.3)

Доказательство:

Извлекая корень из первой и последней части неравенства, получим требуемое неравенство.

Следствие:

Доказательство:

, тогда

49.3 Линейная независимость системы попарно ортогональных векторов

Определение: Элементы a и b ортогональны, если

Теорема: имеется система элементов . Если при и , то линейно независима.

Доказательство:

Пусть для некоторых действительных (49.4).

Помножим скалярно обе части равенства (49.4) на . Так как ( ортогональна всем остальным ), то все слагаемые суммы в левой части (49.4), кроме k-ого, обращены в ноль, т.е. это равенство станет иметь вид:

откуда (49.5)

Из равенства (49.5) следует, что система -линейно независима.

Определение: базис является ортогональным базисом, в примерах ЕП если все её элементы попарно ортогональны, а если его элементы имеют единичную длину (ортонормированны), то базис называется ортонормированным (в дальнейшем - ОНБ).

Определение: пусть в линейном пространстве задано некоторое количество элементов . Линейной оболочкой (ЛО) этого множества называется множество всех элементов b, которые можно линейно выразить через заданные элементы .

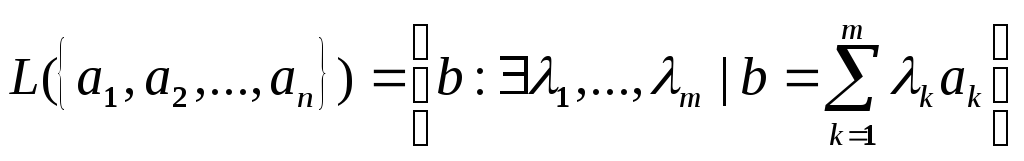
49.4 Ортогонализация Шмидта

Теорема: пусть задан базис . Тогда существует ортонормированный базис (ОНБ) такой, что ЛО его и заданного базиса равны, т.е.

при kn

Доказательство:

Пусть , положим

Тогда:

и ,т.е. ортогонален как и , так и . По аналогии методом математической индукции читателю предлагается самостоятельно установить, что всякий элемент в базисе Шмидта ортогонален всем предыдущим , и поэтому базис - ортогональный.

49.5 Конечномерные и бесконечномерные Евклидовы пространства

Пусть задан базис и (49.9)

При этом является скалярным произведением (показать самостоятельно, что 4 свойства ЕП выполнены). Полученное произведение есть конечномерное Евклидово пространство. Мы показали, что всякое конечномерное линейное пространство может быть сделано Евклидовым.

Бесконечномерным Евклидовым пространством является, например, множество функций, непрерывных на отрезке со скалярным произведением , ибо следующая бесконечная последовательность является ортоногональной и, следовательно, линейно независимой.

Читателю предлагается самостоятельно устанавливать предыдущее утверждение относительно примера бесконечномерного евклидова пространства, (проверить выполнение всех свойств скалярного произведения) а также показать, почему множество всех интегрируемых (по Риману) функций на отрезке не является евклидовым пространством (не выполняется свойство; при этом считается, что)

49.6 Комплексные евклидовы пространства

Если два элемента (вектора) некоторого ЕП заданы комплексными координатами (например: ), то они находятся в комплексном ЕП.

При этом в комплексном ЕП свойство 1) заменяется на:

(- число, комплексно сопряженное к с)

а свойства 2), 3) и 4) скалярного произведения остаются без изменения.

При этом: (49.6)

В самом деле, и (49.6) доказано.

Надо иметь в виду, что:

Замечание 1: 4 свойства действительного ЕП в комплексном ЕП не могут иметь места, ибо они противоречат друг другу, так как , что не соответствует свойству 4. ( при любом a≠0)

Поэтому свойство 1) для комплексных ЕП слегка изменится, а остальные останутся в силе

Замечание 2: Невозможно также определить угол между элементами комплексного ЕП, ибо величина , вообще говоря, будет комплексной и может не быть косинусом некоторого вещественного угла.

В качестве примера советуем показать читателю, что если и - координаты соответственно векторов a и b по базису , то тогда - является скалярным произведением (и, следовательно, конечномерное линейное комплексное пространство становится евклидовым), а будет ортонормированным базисом относительно заданного скалярного произведения.