§9. Элементарное преобразование матриц

9.1 Понятие элементарного преобразования

Определение 9.1: Элементарным преобразованием строк 1-го типа называется:

либо 1) замена строк местами;

либо 2) умножение строки на число ;

либо 3) сложение строк.

Определение 9.2: Элементарным преобразованием строк 2-го типа называется 1 из 2-х действий:

либо 1) замена строк местами;

либо 2) прибавление к одной строке другой, умноженной на некоторое число.

Аналогично определяются элементарные преобразования столбцов 1-го и 2-го типа.

9.2 Эквивалентные матрицы и системы

Определение 9.3: Матрицы А и В называются эквивалентными, если одну из них можно получить из другой с помощью конечного числа элементарных преобразований строк.

Соответственно различают эквивалентности первого и второго типа.

Определение 9.4: Системы линейных уравнений называются эквивалентными, если эквивалентны их расширенные матрицы.

Читателю предлагается доказать самостоятельно, что эквивалентные системы линейных уравнений имеют одно и то же множество решений.

Свойства:

(предлагаем читателю вывести их самостоятельно)

1. А~А /рефлексивность/

2. А~ВВ~А /симметричность/

3. А~В, В~СА~С /транзитивность/

9.3 Ступенчатые матрицы; сведение матрицы к ступенчатой

Определение 9.5: Ступенчатой называется матрица такого вида:

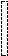
этого столбца (столбцов) могло и не быть

/при переходе к следующей строке «вниз» идем не более, чем на один ненулевой элемент; слева направо последующая строка может увеличиться и на несколько нулевых элементов/

Нулевая матрица, по определению, также является ступенчатой.

Справедлива следующая теорема Гаусса:

Всякая матрица эквивалентна некоторой ступенчатой матрице.

Эту теорему доказываем методом математической индукции по числу строк матрицы А:

1. n=2, т.е. ;

Не ограничивая общности, можно считать, что , ибо если , а , то меняем местами первую и вторую строки.

Из второй строки матрицы А вычтем первую, умноженную на . Получим:

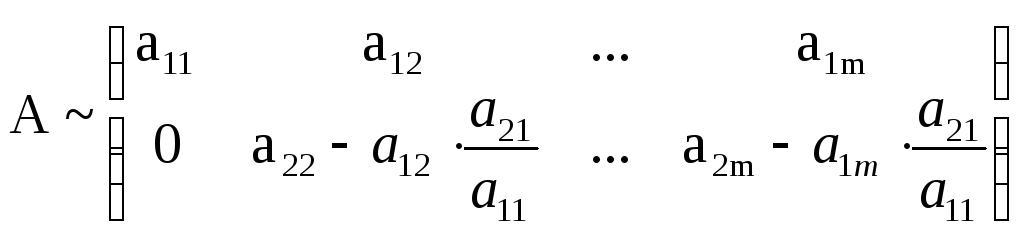
— ступенчатая матрица.

2. Шаг индукции. Пусть .

Можно считать, что первый столбец матрицы А ненулевой, т.е. при некотором j. Тогда, меняя, в случае необходимости первую и j-ую строки местами, получим, что (для новой матрицы). Вычитая из j-й строки (j=2,3,...,k,k+1) первую, умноженную на , получим:

–– ступенчатая матрица.

Матрица, получившаяся в правом нижнем углу матрицы А, состоит из k строк, и поэтому она сводится к ступенчатой по индуктивному предположению.

Теорема Гаусса доказана.

9.4 Диагональные матрицы

Определение 9.6: Матрица называется диагональной, если все её элементы, стоящие вне главной диагонали, равны нулю.

Имеет место следующая теорема:

Всякая невырожденная матрица эквивалентна некоторой диагональной и единичной.

Теорему доказываем методом математической индукции по порядку матрицы.

1. База индукции: пусть n=2.

, т.е.

Из 1-ой строки вычитаем 2-ую, умноженную на – диагональная матрица.

2. Шаг индукции:

Заметим, что (более того, для любого j=1,2,…,k,k+1), ибо (см параграф 3 , п.3.3) . Тогда, вычитая из j-ой строки (k+1)-ю (j=1,2,…,k), умноженную на , получим, что:

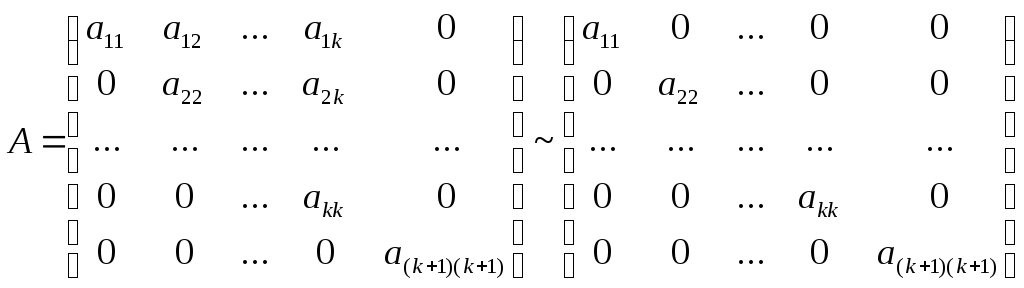
(9.1)

матрица k-го порядка, которая, по индуктивному предположению, сводится к диагональной.

А поделив j-ю строку (j=1,2,…,k,k+1) на (как уже отмечалось ранее, для любого j), получим единичную матрицу.

Теорема доказана.