
- •Введение
- •1.3 Первые 10 свойств определителя
- •2) При замене строк или столбцов местами определитель меняет знак:
- •4) Постоянный множитель элементов строки/столбца можно вынести за знак определителя:
- •§2. Миноры и дополнения
- •§3. Определитель n-го порядка
- •3.1 Метод математической индукции
- •3.2 Вычисление определителя n-го порядка по минорам и ад
- •3.3 Верхне треугольный определитель
- •Глава 2. Матрицы и системы линейных уравнений §4. Определение матрицы, равенство, операции над матрицами
- •4.1 Определение матрицы
- •4.2 Сложение матриц
- •§5. Произведение матриц
- •5.1 Свойства операции суммы
- •5.2 Определение произведения матриц и его некоммутативность
- •5.3 Ассоциативность произведения матриц
- •5.4 Правая и Левая дистрибутивность умножения матриц относительно сложения
- •5.5 Транспонирование произведения
- •5.6 Определитель произведения
- •5.7 Вырожденная и невырожденная квадратная матрица
- •5.8 Единичная матрица и её свойства
- •5.9.Определение обратной матрицы; отсутствие обратной матрицы у вырожденной
- •5.10 Теорема о существовании обратной матрицы и алгоритм её нахождения
- •§6. Системы линейных уравнений
- •6.1 Определенность системы линейных уравнений. Совместность, несовместность
- •6.2 Матричная форма записи m линейных уравнений с n неизвестными
- •§7. Системы n линейных уравнений с n неизвестными их решение с помощью обратной матрицы
- •§8. Формула Крамера
- •§9. Элементарное преобразование матриц
- •9.1 Понятие элементарного преобразования
- •9.2 Эквивалентные матрицы и системы
- •9.3 Ступенчатые матрицы; сведение матрицы к ступенчатой
- •9.4 Диагональные матрицы
- •§10. (Метод Гаусса) Решение произвольной системы линейных уравнений
- •§11. Определение ранга матрицы
- •11.1 Понятие ранга матрицы
- •11.2 Инвариантность ранга при элементарных преобразованиях
- •Глава 3. Векторная алгебра §14.Векторы, равенство векторов , коллиниарность и компланарность векторов, разность , умножение векторов. Свойства этих операций.
- •14.1 Сложение векторов
- •14.2 Умножение вектора на число
- •14.3 Свойства линейного пространства
- •2) Ассоциативность
- •§15. Линейно – зависимые векторы и их свойства
- •§17. Базис, координаты вектора, разложение вектора по базису
- •Эта система линейно независима;
- •Любой вектор можно выразить через , причём это выражение единственно.
- •§18. Линейное пространство и линейные операторы
- •Шаг индукции
- •Линейное подпространство
- •Линейный оператор
- •§19. Исследование систем линейных уравнений
- •19.1. Однородные системы
- •19.2 Решение неоднородных систем
- •19.3 Доказательство достаточности теоремы Кронеккер-Капелли
- •19.4 Доказательство критерия определённости системы
- •§20. Ортонормированный базис
- •§21. Прямоугольная декартова система координат. Координаты точки. Определение координат вектора по координатам его начала и конца. Расстояние между двумя точками
- •§22. Деление отрезка в заданном отношении
- •25.2 Свойства векторного произведения .(антикоммутативность, линейность и однородность)
- •Доказательство Леммы 25.1:
- •27.3 Свойства смешанного произведения
- •27.4Необходимое и достаточное условие компланарности трех векторов
- •§28 Смешанное произведение векторов в координатной форме
5.6 Определитель произведения
Справедлива следующая (дающаяся без
доказательства) теорема: определитель
произведения матриц равен произведению
определителей: det(A![]() B)=detA
B)=detA![]() detB.
(5.15)
detB.
(5.15)
5.7 Вырожденная и невырожденная квадратная матрица
Определение: квадратная матрица называется вырожденной, если её определитель равен нулю, и невырожденной, если её определитель не равен нулю.
5.8 Единичная матрица и её свойства
Определение: квадратная матрица, все элементы которой, стоящие на главной диагонали, равны единицы, а остальные – нулю, т.е. матрица вида:
 (5.16)
(5.16)
называется единичной матрицей.
Элементы единичной матрицы обозначаются символом Кронекера:
 (5.17)
(5.17)
Справедлива теорема:
![]() будет:
будет:
![]() .
(5.18)
.
(5.18)
Доказательство
Пусть: А=![]()
![]() и
и
![]()
![]() . Покажем, что
. Покажем, что
![]() .
.
В самом деле,
 , т.е. В=А.
, т.е. В=А.
Для доказательства равенства
![]() используем очевидную формулу
используем очевидную формулу
![]() и равенство (5.12). Получим:
и равенство (5.12). Получим:
![]()
Покажем, всякая матрица
![]() со свойством
со свойством
![]() для любой матрицы А (соответственно, и
всякая матрица
для любой матрицы А (соответственно, и
всякая матрица
![]() со свойством
со свойством
![]() для любой матрицы А), должна совпадать
с определенной в (5.16) матрицей Е. В самом
деле,
для любой матрицы А), должна совпадать
с определенной в (5.16) матрицей Е. В самом
деле,
![]() и
и
![]() ,
т.е. матрица, удовлетворяющая свойству
(5.18), единственна и задаётся формулой
(5.16)
,
т.е. матрица, удовлетворяющая свойству
(5.18), единственна и задаётся формулой
(5.16)
5.9.Определение обратной матрицы; отсутствие обратной матрицы у вырожденной
Пусть А=![]()
![]() – квадратная матрица.
– квадратная матрица.
Определение: матрица
![]() называется обратной к матрице
А, если выполнено равенство
называется обратной к матрице
А, если выполнено равенство
![]() .
(5.19)
.
(5.19)
Отметим, что вырожденная матрица обратной
иметь не может, ибо если detA=0,
то из (5.19) и (5.15) имеем:
![]() (противоречие).
(противоречие).
5.10 Теорема о существовании обратной матрицы и алгоритм её нахождения
Имеет место следующая теорема:
Всякая невырожденная матрица А=![]()
![]() имеет обратную матрицу
имеет обратную матрицу
![]() =
=
=
=![]()
![]() ,
элементы которой находят по формуле:
,
элементы которой находят по формуле:
![]() (5.20)
(5.20)
![]() ,
а
,
а
![]() –
её алгебраические дополнения.
–
её алгебраические дополнения.
Доказательство теоремы:
Пусть
![]()
![]() .
Тогда:
.
Тогда:
(5.20) (5.3)
![]() (5.21)
(5.21)
Используем далее 11-е и 12-е свойства определителей (см. §2.2 и §2.3). Если i=j, то
![]() ,
(5.22)
,
(5.22)
ибо последняя сумма является разложением определителя Δ по его i-й строке.
В случае
![]() будет
будет
![]() (5.23)
(5.23)
(сумма произведений элементов i-й
строки на алгебраические дополнения
другой j-й строки
![]() см. 12-е св-во), и тогда
см. 12-е св-во), и тогда
![]() ,
если
,
если
![]() .
.
Сопоставляя (5.22) и (5.23), имеем:
 ,
т.е. В=Е, и теорема доказана.
,
т.е. В=Е, и теорема доказана.
Равенство
![]() читателю предлагается доказать
самостоятельно (в этом случае определитель
Δ в равенстве (5.22) будет разлагаться по
j-му столбцу).
читателю предлагается доказать
самостоятельно (в этом случае определитель
Δ в равенстве (5.22) будет разлагаться по
j-му столбцу).
Отметим, что определенная формулой
(5.20) обратная матрица единственна, ибо
если
![]() и
и
![]() – такие матрицы, что
– такие матрицы, что
![]() ,
то
,
то
![]() ,
и
,
и
![]() ,
т.е.
,
т.е.
![]() =
=![]() =
=![]() .
.
Покажем также, что
![]() (5.24)
(5.24)
В самом деле:
![]() ,
и (5.24) доказано.
,
и (5.24) доказано.
Итак, мы показали справедливость следующих свойств произведений матриц:
-
 ;
; -
 и
и
 ;
; -
 ;
; -
det(A
 B)=detA
B)=detA detB;
detB; -
 ;
; -
 ;
; -
 ;
; -
 .
.
Свойства 1) ÷ 6) были доказаны ранее.
Свойство 7) очевидно, ибо если 0=В =![]()
![]() с
с
![]() для любых l и j,
то для произведения
для любых l и j,
то для произведения
![]()
![]() имеем:
имеем:
![]() для любых i и j,
т.е. С=0.
для любых i и j,
т.е. С=0.
Покажем свойство 8):
Пусть А =![]()
![]() ;
В =
;
В =![]()
![]() .
.
Тогда произведение
![]()
![]() c
c
![]() .
(5.25)
.
(5.25)
Также:
![]()
![]() с
с
![]() ;
(5.26)
;
(5.26)
![]()
![]() с
с
![]() (5.27)
(5.27)
и
![]()
![]() c
c
![]() .
(5.28)
.
(5.28)
![]()
![]() c
c
![]() ;
(5.29)
;
(5.29)
![]()
![]() c
c
![]() .
(5.30)
.
(5.30)
Из равенства (5.30) имеем:
(5.27) (5.3) (5.25) (5.28)
![]() ,
,
(5.28) (5.25) (5.3) (5.26) (5.29)
и
![]() ,
,
т.е. P=G=H,
или
![]() ,
и свойство 8) доказано.
,
и свойство 8) доказано.
Алгоритм нахождения обратной матрицы
Из формулы (5.20), чтобы найти обратную
матрицу
![]() ,
нужно:
,
нужно:
-
найти детерминант матрицы А; если он равен нулю, то обратной нет. Если detA
 0,
то находим
0,
то находим
-
матрицу
 из алгебраических дополнений;
из алгебраических дополнений; -
транспонируем эту матрицу
 ;
; -
всякий элемент матрицы
 делим на detA, получим
матрицу
делим на detA, получим
матрицу
 .
.
Рассмотрим пример: Пусть
![]() .
Найдем обратную матрицу
.
Найдем обратную матрицу
![]() :
:
-
detA = –2
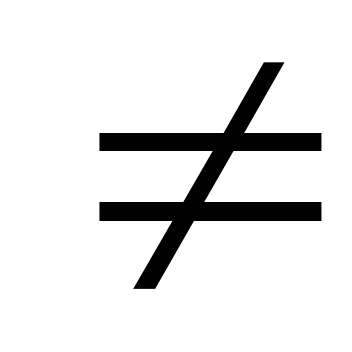 0;
0; -
дополнения:
 ;
;
 ;
;
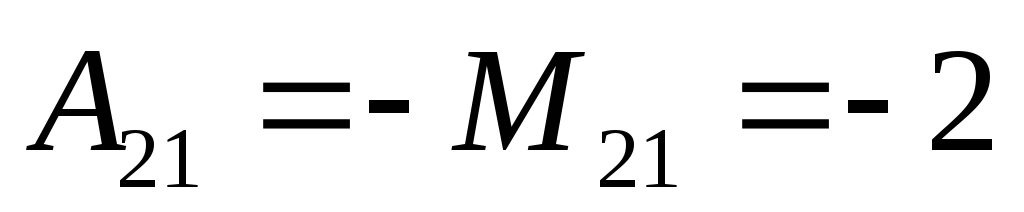 ;
;
 и
и
 ;
; -
 ;
; -
 .
.
