19.2 Решение неоднородных систем

Теорема 19.3: Общее решение неоднородной системы (19.1) представляется в виде сумм частного решения (19.1) и общего решения соответствующей однородной системы (19.7).

Доказательство: Если – некоторое частное решение системы (19.1), то для любого

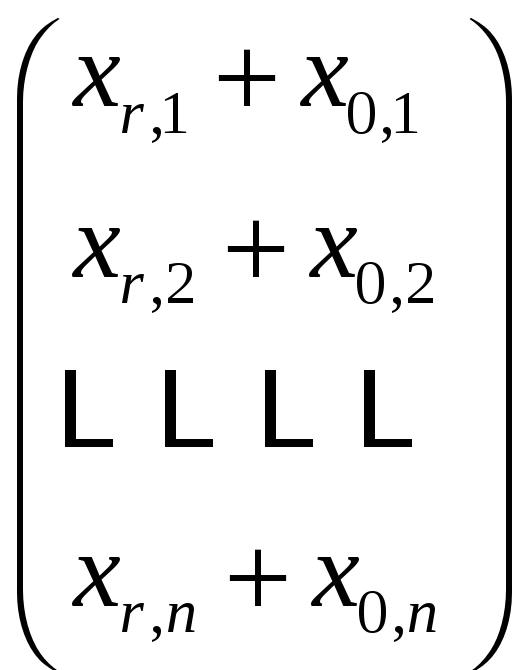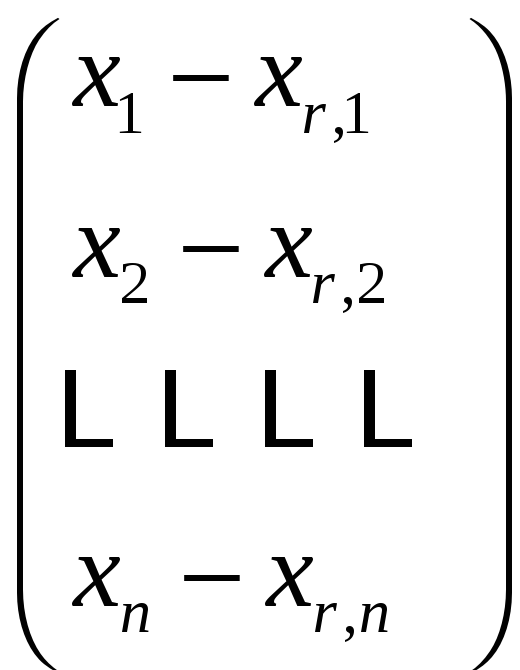
решения системы (19.7) по теореме 19.1 имеем, что является решением системы (19.1). Наоборот, для любого решения системы (19.1) из теоремы 19.1 имеем, что разность является решением соответствующей однородной системы (19.7).

Теорема 19.3 доказана.

19.3 Доказательство достаточности теоремы Кронеккер-Капелли

Полагая в системе (19.2): Ax = b все свободные неизвестные нулями, получим систему: (19.18),

где – матрица базисного минора. А так как это матрица невырожденная, то система (19.18) (и система (19.2)) имеет решение.

19.4 Доказательство критерия определённости системы

Если n = r , то по теореме 19.2 множество решений однородной системы (19.7) имеет размерность, равную нулю, то есть решение однородной системы состоит только из одного нулевого решения. Тогда, по теореме 19.3 всякие решения системы (19.1) состоят только из одного частного решения, то есть оно единственно, и поэтому система (19.1) является определённой.

§20. Ортонормированный базис

Определение: Векторы и – ортогональные, если они перпендикулярны друг другу.

Определение: Базис является ортогональным, если все его векторы попарно перпендикулярны.

Определение: Базис является ортонормированным, если он ортогонален и все векторы в нём имеют единичную длину.

Если базис ортонормированный, то

Где - проекция вектора на вектор (для вывода этой формулы надо внимательно разобрать доказательства всех теорем из §16.1, когда - ортонормированный базис ) для теорем 16.3, а так же -ортонормированный базис (для теорем 16.2) либо для теорем 16.1

Тогда из §17 получим

следующие свойства проекции вектора на вектор:

Рис 20.1

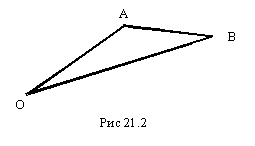
§21. Прямоугольная декартова система координат. Координаты точки. Определение координат вектора по координатам его начала и конца. Расстояние между двумя точками

Координаты точки – это координаты вектора ОМ (где О – начало координат

(см. рис 21.1)), т.е. (см. рис. 21.2)

тогда, если и, z

т.е. и ,

то y

x

Рис 21.1

В §24 будет показано, что длина вектора

(21.2)

Тогда расстояние между точками A и B:

(21.3)

(расстояние между точками А и В – это длина вектора АВ)

§22. Деление отрезка в заданном отношении

Если ,,и М Точка М делит отрезок АВ в отношении , если (22.4)

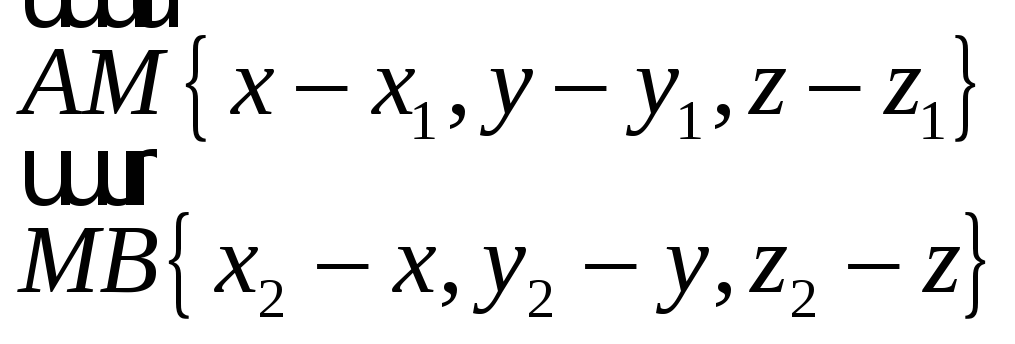
и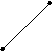з (22.4) имеем:

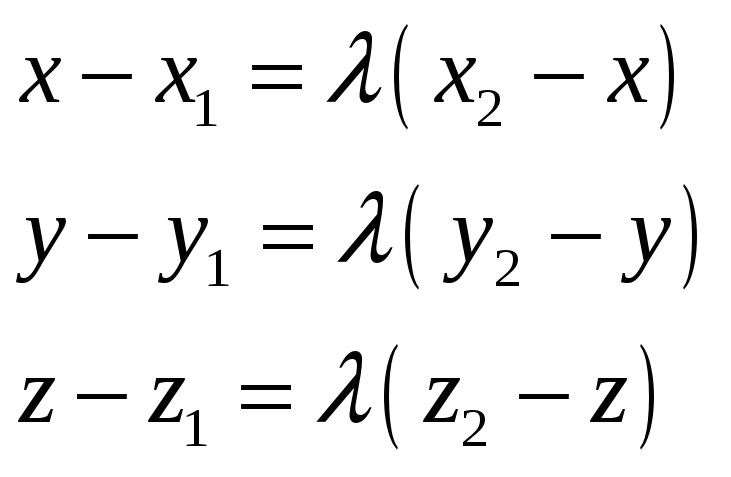(22.5)

преобразуем формулы (22.5) до вида Рис 22.1

Если то М - середина отрезка, то ее координаты которой вычисляются по формулам(ибо тогда

§23. Скалярное произведение векторов и его свойства

Определение:

(23.6) – скалярное произведение

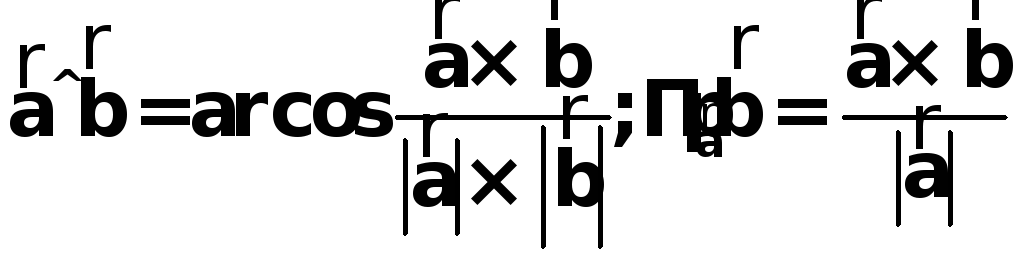
Свойства скалярного произведения:

1. 

2. 

3. 

4. 

Величина называется скалярным квадратом вектора. По определению:

(23.9)

Доказательство 2-го свойства:

Доказательство 3-го свойства:

Условие ортогональности 2-х векторов:

Если 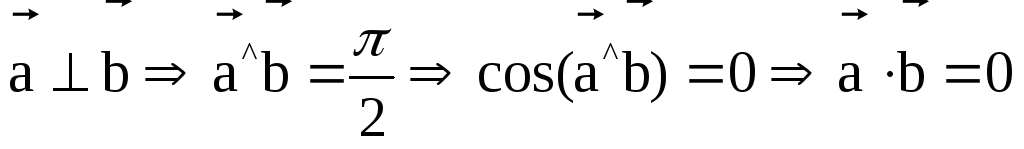. Вывод .

§24. Вычисление скалярного произведения векторов через координаты сомножителей

24.1 Вычисление скалярного произведения через координаты сомножителей

Пусть

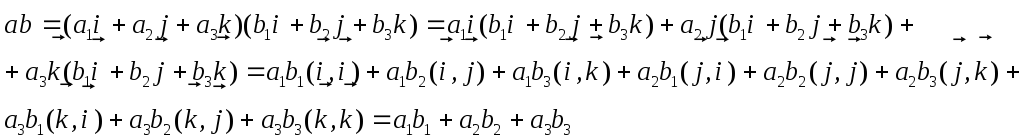
Ибо 1=и так как

Тоесть (24.9)

24.2 Доказательство формулы

Пусть , тогда из(24.9) имеем (24.10)

24.3 Вычисление угла между векторами

(24.11)

Смотрите формулы (23.6), (24.9), (24.10)

24.4 Проекция вектора на ось, коллинеарную вектору

Смотрите формулы (23.6), (24.9), (24.10)

, (24.12)

=0 (24.13) далее формула

(либо в этом случае ,далее формула (23.6))

(здесь уже , затем используем равенство (23.6)

§25. Векторное произведение и его свойства

25.1 Определение векторного произведения

Обозначение векторного произведения :

при этом , по определению.

1) ,

2)

S-площадь параллелограмма OADB B

D

О

А

Рис 25.1

Направление вектора определяется по “правилу правой руки”: если большой палец правой руки направлен по вектору , а указательный по вектору , то ладонь укажет направление векторного произведения.

Его также можно определить по “правилу правого винта” или “Буравчика”: векторное произведение направленно в сторону движения правого винта , если его вращать от вектора к вектору .