1. Эта система линейно независима;

2. Любой вектор можно выразить через , причём это выражение единственно.

Доказательство:

Т.к. – линейно зависима, то при (17.1)

Если , то из (17.1) получим, что и , т.е. система – линейно зависима, чего не может быть, т.к. она является базисом.

Поэтому , и, поделив обе части (17.1) на и перенося слагаемые в правую часть, получим, что с ;…; .

Получим единственность: (17.2)

Если существует другое разложение (17.2): , (17.3)

то, вычитая из (17.2) равенство (17.3), получим:

Но, так как система – л.нез., то мы получаем, что. т.е

Единственность доказана. Доказана также следующая лемма.

Лемма 17.1: если система – л.нез., а – л.з., то элемент “” единственным образом линейно выражается через элементы .

Определение: называются координатами вектора при его разложении по базису

в (17.2)

Теорема 17.2: При сложении векторов их координаты складываются, а при умножение вектора на число – координаты умножаются на это число.

;

Доказательство:

и , тогда и

§18. Линейное пространство и линейные операторы

Определение: Линейное пространство над множеством вещественных чисел – некоторое множество объектов, где заданы операции сложения и умножения на действительное число, со следующими свойствами:

1. 

2. 

3. 

4. , тогда

5. 

6. 

7. 

8. 

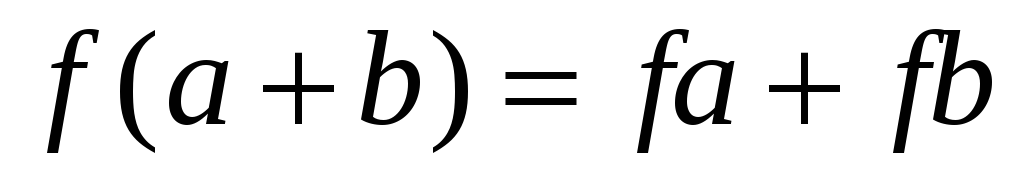
В линейном пространстве действуют все определения и теоремы §15 и §17.

Теорема 18.1: Система линейно зависима, когда хотя бы один из её элементов можно выразить через остальные.

Доказательство такое же, как и у векторов. Система линейно независима, если из того , что .(т.е содержит ненулевой элемент)

Определение18.1 Если в нетривиальном пространстве существует базис, то пространство называется конечномерным.

Определение18.2: Число элементов базиса – размерность линейного пространства.

Теорема 18.2: Все базисы одного и того же пространства состоят из одинакового количества элементов.

Теорема 18.2 будет доказана ниже (как следствие теоремы о замене элементов базиса).

Из неё, в частности, следует корректность определения размерности линейного пространства и её независимость от выбора базиса.

Определение 18.3: Линейной оболочкой называется множество всех элементов линейного пространства, которые линейно выражаются через .

Определение18.4: Систему назовем полной ,если все линейное пространство является ее линейной оболочкой т.о. Базис - полная линейно не зависимая система элементов.

Теорема 18.3: Координаты суммы равны сумме координат.(доказывается аналогично теореме 17.2)

Теорема о замене элементов базиса:

- базис (18.1)

- линейно независимая система (18.2)

Тогда некоторые m элементы (18.1) заменяются на элементы (18.2)

(18.3) (причём система (18.3) будет базисом)

Согласно определениям §17, базис дополнить нельзя, ибо, любые его дополнения делают его линейно зависимой системой. т.е из теоремы 18.2 получается из теорема о замене элементов базиса.

Следствие18.1: Любую линейно независимую систему в конечномерном линейном пространстве можно дополнить до базиса.

Лемма 18.1:

Доказательство леммы 18.1:

(18.4)

(18.5)

Подставляя в (18.5) вместо b его выражение из формулы (18.4), получим

(18.6)

Лемма 18.2:

(18.7)

Доказательство:

(18.8)

(18.9)

Поместив вместо a в (18.9) его выражение по формуле (18.8), получим:

Следствие: Всякую полную систему можно уменьшить до базиса.

Доказательство теоремы о замене элементов базиса методом математической индукции:

m=1 (база индукции)

Тогда можно считать, что

т.к. (18.1) – базис, то .

Тогда, по лемме 18.1 , т.е. система – полная.

Допустим, что линейно зависима. Тогда по лемме 17.1

Но т.к., то по лемме 18.2: , и система – л.з.

Следовательно, предположение о линейной зависимости системы неверно.