3.1. Понятие о режущей кромке лезвия, ее расчет, трансформация и режимы резания

По вопросу, как определять размер (толщину) режущей кромки лезвия и что считать этим параметром лезвия в технической литературе, имеется ряд соображений и расчетных формул, которые описывают реальность с вероятностью от 0,55 до 0,85, т.е. с ошибками от 45 до 15%.

Целесообразно рассмотреть соображения и расчетную формулу, которые отражают реальность с вероятностью 0,85, достаточную для инженерных расчетов.

В

Рис. 3.1

оспользуемся рис. 3.1, где представлена принципиальная схема сечения лезвия, работающего в «рубящем» режиме, когда угол между направлением нормальной силы F_н и направлением перемещения V равен углу трения φ, т.е. ε = φ. При этом:

δ = 2 r sin φ, (3.1)

где δ – толщина режущей кромки; r – радиус ее закругления; φ – угол трения разрезаемого материала по режущей кромке лезвия.

Приведенная формула (3.1) связывает свойства материала φ с параметрами δ и r, образующимися при износах режущей кромки. Поэтому она объективнее отражает суть дела.

Важно также иметь в виду, что при перемещении лезвия под разными углами относительно разрезаемого материала толщина режущей кромки его трансформируется, как показано на рис. 3.2, из этого следует, что δ_n в сечении n–n оказывается больше, чем δ_n' в сечении n'–n'. Это имеет важное значение с точки зрения затрат энергии при выполнении технологических процессов режущими кромками лезвий.

Рис. 3.2 Рис. 3.3

Эти процессы могут быть трех видов. Их принято называть режимами. Они представлены на рис. 3.3.

а) при ε = 0 – рубящее резание. F_н совпадает с V. Материал разрушается под действием F_н – нормальной силы;

б) при ε > φ – резание со скольжением. Частица m скользит по режущей кромке под действием F_т – F_max. Разрушение материала происходит по направлению F_r. Здесь φ – угол трения материала о режущую кромку лезвия;

в) при 0 < ε  φ – резание без скольжения с продольным перемещением. Частица m перемещается под действием F_V до разрушения, поскольку ε < φ, а F_т = F из условия F_т = F_н tg ε, которая меньше F_max = F_н tg φ.

С точки зрения затрат энергии выгоднее всех режим «б».

3.2. Определение коэффициентов скольжения сельскохозяйственных материалов по режущим кромкам лезвий

У

Рис. 3.4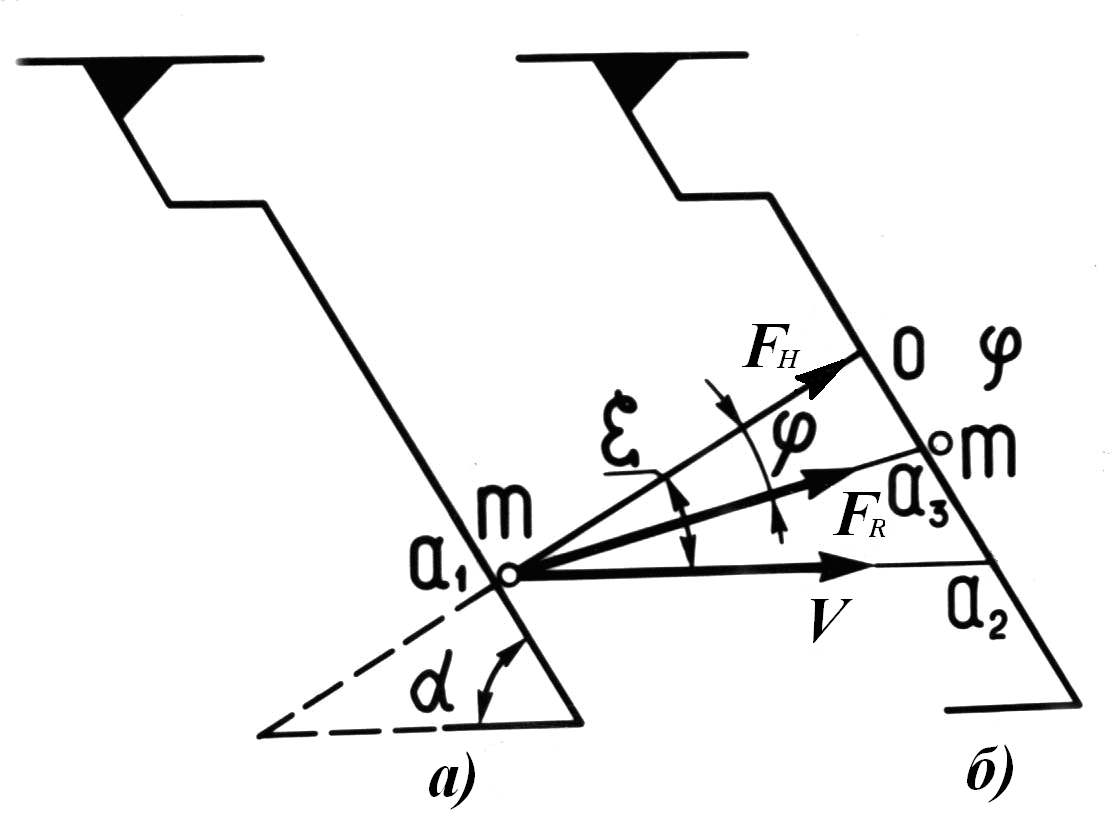

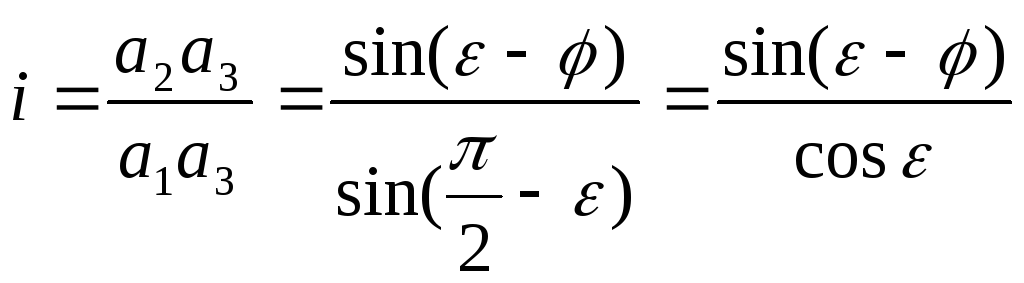казанный коэффициент связан с выбором углов установки лезвий к направлению перемещения их режущих кромок таким образом, чтобы они не забивались почвой и растительными остатками, т.е. для обеспечения нормального технологического процесса рабочих органов почвообрабатывающих и других орудий и машин. Рассмотрим это на примере черенкового ножа, перемещающеегося из положения «а» в положение «б» на рис. 3.4. При этом в точке а₁ на частицу m действуют: сила нормальная F_н, результирующая F_r, отклоненная от F_н на угол трения φ, и сила F_V, действующая по направлению V и отклоненная от него на угол ε. Под действием силы F_r частица m из точки а₁ переместится в точку а₃, что составит величину абсолютного ее перемещения. В то же время, двигаясь по направлению V, точка m окажется в точке а₂ и величина а₂а₃ отразит путь m в относительном движении вдоль режущей кромки лезвия. Имея это в виду, на основании рис. 3.4 по известной теореме синусов записываем:

, (3.2)

где i – искомый коэффициент скольжения.

Чем он больше, тем лучше с точки зрения незабиваемости режущих кромок лезвий обрабатываемым материалом. При этом используется условие скольжения, при котором ε  φ или /2 – γ  φ, где γ – угол установки режущей кромки лезвия к направлению его перемещения (в нашем случае α = γ, т.е. α < < /2 – φ).

Зная это, можно определять углы установки режущих кромок лезвий к направлениям их перемещений и исключать, таким образом, их забивание.