§4. Работа при изопроцессах.
Изохорный процесс (V = сonst).
Так как система не изменяет своего объема, она не совершает работы над внешними телами
; А=0
, тогда
, (3.4.1)
При изохорном процессе работа газом не совершается, а поступающее (или отдаваемое) тепло равно изменению внутренней энергии.
Изобарный процесс (P=сonst).
При постоянном
давлении объем системы меняется, и она
может совершать работу
,
. (3.4.2)
Используя уравнение
состояния идеального газа
(P
= Const),
можно записать
. (3.4.3)
Из I начала термодинамики
,
откуда
. (3.4.4)
При изобарическом процессе часть поступающего тепла расходуется на увеличение внутренней энергии, а часть – на совершение макроскопической работы.
Изотермический процесс (T = сonst)
При изотермическом
процессе температура системы не меняется
и, следовательно
.
Тогда из I
начала термодинамики
,
,
т.е.
,
или Q
= A΄.
Из уравнения состояния идеального газа
можно выразить Р:
,
тогда
и
. (3.4.5)
Следовательно,
.
При изотермическом процессе внутренняя энергия газа не меняется, вся полученная теплота идет на совершение работы.
Адиабатический
процесс (
).
При адиабатическом
процессе к системе не подводится теплота.
В этом случае
.
Из уравнения адиабаты
давление
.
Тогда
и
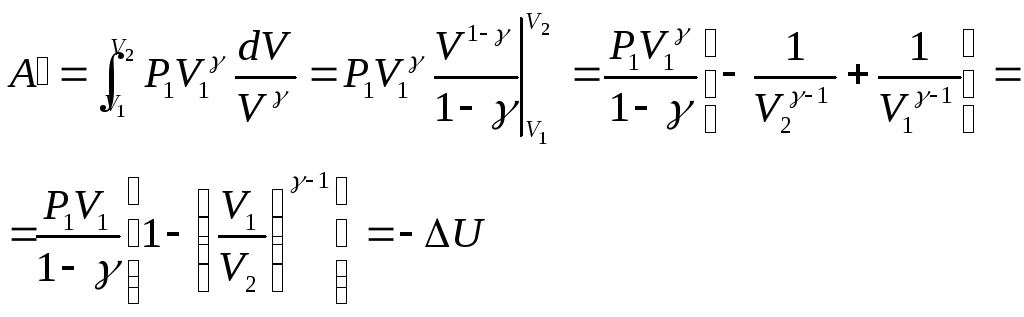. (3.4.6)
При адиабатическом процессе работа совершается газом за счет уменьшения его внутренней энергии.
Найдем выражение
для вычисления работы в политропическом
процессе. Будем использовать уравнение
политропы в параметрах (p,V).
Если известны значения давления и объема
в некотором состоянии
,
тогда
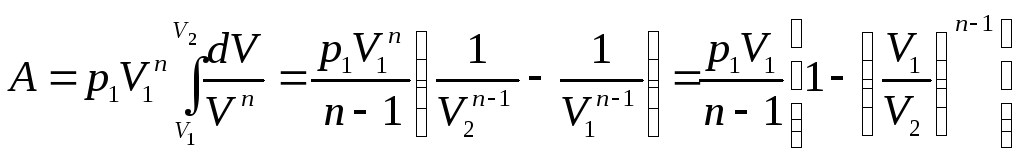. (3.4.7.)
Покажем, что
изотермический, изобарный, изохорный
и адиабатный процессы являются частными
случаями политропического процесса. В
адиабатном процессе
,
следовательно
и уравнения политропы (3.3.12), (3.3.13), (3.3.14)
переходят в уравнения адиабаты в виде
(3.3.4), (3.3.5) и (3.3.6) соответственно.
Теплоемкость при
изотермическом процессе равна
бесконечности, следовательно
.
Из уравнений (3.3.12) и (3.3.14) получаем условие
,
а выражение (3.3.13) переходит в закон
Бойля-Мариотта
.
Показатель политропы в изобарном
процессе равен нулю, поэтому из (3.3.12)
получаем уравнение изобары
.
Для изохорного процесса показатель
.
Уравнение политропы (3.3.14) преобразуем
к виду
, (3.4.8)
откуда получается
уравнение изохоры
.
Рассмотрим процесс
не являющийся квазиравновесным –
расширение газа в пустоту. Пусть имеется
сосуд в адиабатически изолированной
оболочке, разделенный на две части. В
одной части давление
и температура
,
в другой части газа нет. Если перегородку
убрать мгновенно, то возникает
неравновесное состояние с потоками
частиц, отличными от нуля. В дальнейшем,
в процессе выравнивания параметров,
потоки затухают и через некоторый
промежуток времени в сосуде устанавливается
равновесное состояние при температуре
.
Так как перегородка убирается мгновенно,
то газ не совершает работу против внешних
сил; так как система адиабатически
изолирована, количество теплоты газу
не передается и не отнимается,
следовательно, его внутренняя энергия
не изменяется. В модели идеального газа,
это означает, что температура газа
остается постоянной.
К процессу расширения
газа в пустоту нельзя применить результат,
полученный для квазиравновесного
процесса адиабатного расширения, для
которого
.
Применим полученные результаты к анализу процесса распространения звука в газах.