
- •Метод молекулярных орбиталей.
- •Орбитали двухатомной молекулы.
- •Межмолекулярные силы. Силы, обеспечивающие ионную и ковалентную связи, называются химическими. Эти силы убывают с возрастанием расстояния между атомами.
- •Спектры молекул.
- •Итак, полная энергия молекулы определяется выражением
- •Комбинационное рассеяние света.
Спектры молекул.
В то время как спектры излучения атомов состоят из отдельных линий, молекулярные спектры при наблюдении их в прибор средней разрешающей способности представляются состоящими из полос – полосатый спектр.
При более тщательном изучении спектров с помощью приборов высокой разрешающей силы выяснилось, что каждая полоса, в свою очередь, состоит из большого числа близко расположенных линий. Эта особенность молекулярных спектров объясняется наличием различных компонент в энергии молекул.
Атомы в молекуле имеют свои электронные состояния, отличающиеся от тех, что были в изолированных атомах. Изменение энергии молекулы происходит в результате изменений в электронной конфигурации, образующей периферическую часть молекулы. Однако ядра молекул могут различным образом колебаться и вращаться относительно общего центра инерции. С этими видами движения связаны запасы колебательной и вращательной энергии.
В первом приближении полная энергия молекулы может быть представлена в виде:
![]() ,
,
где![]() - энергия, обусловленная электронной
конфигурацией,
- энергия, обусловленная электронной
конфигурацией,
![]() - энергия колебаний молекулы (вибрационная
энергия),
- энергия колебаний молекулы (вибрационная
энергия),
![]() - энергия вращательного движения
(ротационная энергия).
- энергия вращательного движения
(ротационная энергия).
К олебания
одного ядра происходят в поле, образованном
другим ядром молекулы.
олебания
одного ядра происходят в поле, образованном
другим ядром молекулы.
Потенциальный профиль, характеризующий это взаимодействие, имеет вид ассиметричной потенциальной ямы. Аппроксимируя потенциальную яму в области минимума параболой (приближение гармонического осциллятора), можем записать
![]()

 ,
,
где
![]() - колебательное квантовое число,
- колебательное квантовое число,
![]() - классическая частота осциллятора.
- классическая частота осциллятора.
Для колебательного
квантового числа имеется правило отбора
![]() .
Ангармоничность, наступающая при
увеличении интенсивности колебаний,
ведет к тому, что с ростом квантового
числа
.
Ангармоничность, наступающая при
увеличении интенсивности колебаний,
ведет к тому, что с ростом квантового
числа
![]() уровни энергии перестают равноотстоять
друг от друга. Происходит сгущение
энергетических уровней при
уровни энергии перестают равноотстоять
друг от друга. Происходит сгущение
энергетических уровней при
![]() .
Этими эффектами в приближении малых
квантовых чисел можно пренебречь. Однако
учет ангармоничности колебательного
движения в двухатомных молекулах
приводит к приближенному выражению для
колебательной энергии
.
Этими эффектами в приближении малых
квантовых чисел можно пренебречь. Однако
учет ангармоничности колебательного
движения в двухатомных молекулах
приводит к приближенному выражению для
колебательной энергии
![]() ,
,
где
![]() - коэффициент ангармоничности.
- коэффициент ангармоничности.
Энергия, связанная с вращением молекулы, определяется формулой:
![]() ,
,
где
![]() - момент инерции молекулы,
- момент инерции молекулы,
![]() - момент импульса молекулы. Но момент
импульса может быть записан в виде
- момент импульса молекулы. Но момент
импульса может быть записан в виде
![]() ,
,
где
![]() -
вращательное квантовое число.
-
вращательное квантовое число.
Таким образом,![]()
![]() .
.
Соответствующее
правило отбора
![]() .
.
Итак, полная энергия молекулы определяется выражением
![]() .
.
Опыт показывает,
что энергетические расстояния между
вращательными уровнями меньше, чем
между колебательными, которые, в свою
очередь, значительно меньше, чем
расстояния между электронными уровнями
![]() .
.
При сообщении молекуле достаточной энергии она переходит в возбужденное состояние и затем, совершая разрешенный правилами отбора переход в одно из более низких энергетических состояний, излучает фотон:
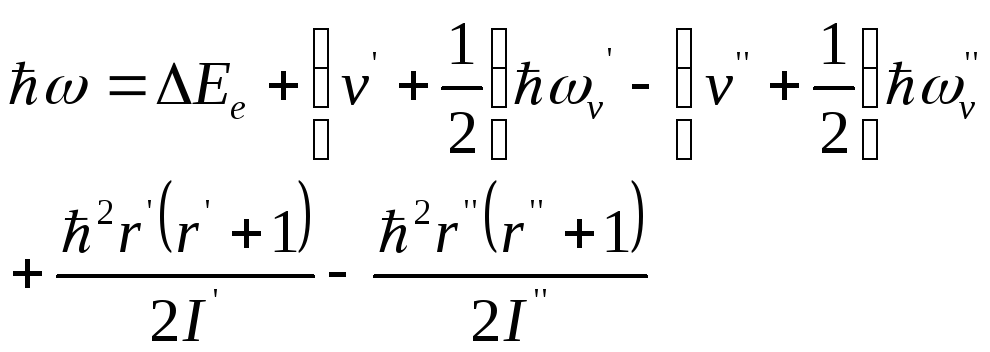 ,
,
(т.к.
![]() и
и
![]() могут отличаться для различных электронных
конфигураций).
могут отличаться для различных электронных
конфигураций).
Если возбуждение
молекул достаточно слабо, то может
происходить только изменение
![]() и, соответственно, в спектрах наблюдаются
только вращательные
полосы. Т.к.
при этом электронная конфигурация и
энергия колебания не меняются, то
и, соответственно, в спектрах наблюдаются
только вращательные
полосы. Т.к.
при этом электронная конфигурация и
энергия колебания не меняются, то
![]() .
.
С учетом правила
отбора
![]() ,
где
,
где
![]() - квантовое число уровня, на который
происходит переход, получим
- квантовое число уровня, на который
происходит переход, получим
![]() ,
откуда
,
откуда
![]() ,
,
где
![]() .
.
Таким образом,
вращательный спектр состоит из ряда
равноотстоящих линий, расположенных в
инфракрасной области спектра. Определив
экспериментально
![]() - расстояние между линиями вращательного
спектра, можно найти
- расстояние между линиями вращательного
спектра, можно найти
![]() - момент инерции молекул (
- момент инерции молекул (![]() рад/с
– из опыта).
рад/с
– из опыта).
Если возбуждение
молекул увеличить, то будут наблюдаться
колебательно-вращательные
полосы. При
этом изменяются и колебательное и
вращательное состояния молекулы.
Поскольку
![]() ,
то переходы, связанные с излучением,
могут наблюдаться не только тогда, когда
,
то переходы, связанные с излучением,
могут наблюдаться не только тогда, когда
![]() ,
но и когда
,
но и когда
![]() .
Энергия перехода
.
Энергия перехода
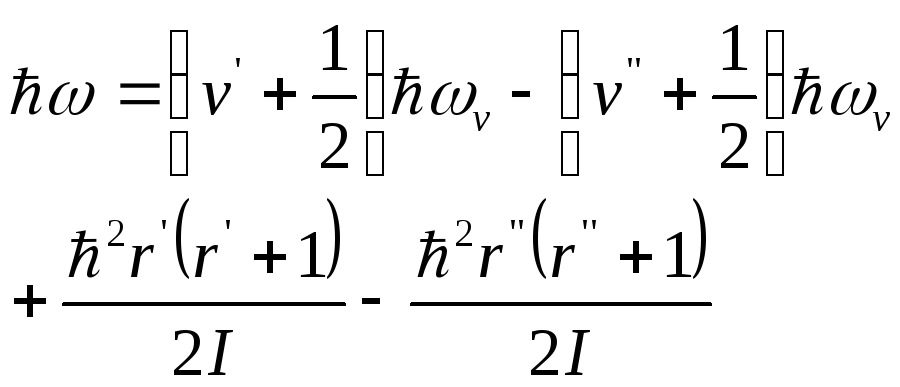 ;
;
отсюда при
![]()
![]() ,
,
п ри
ри
![]()
![]() ,
где
,
где
![]() ,
,
![]() - вращательное квантовое число нижнего
уровня.
- вращательное квантовое число нижнего
уровня.
Совокупность линий
с частотами
![]() называется колебательно-вращательной
полосой. Колебательная частота
называется колебательно-вращательной
полосой. Колебательная частота
![]() определяет положение полосы, а вращательная
часть – структуру полосы (ее расщепление).
определяет положение полосы, а вращательная
часть – структуру полосы (ее расщепление).
Спектральная область, в которой обычно наблюдаются колебательно-вращательные полосы - 8000÷50000 Å.
Вращательные и вращательно-колебательные спектры наблюдаются только у несимметричных двухатомных молекул. Поскольку у симметричных молекул дипольный момент равен нулю и, значит, вращательные уровни отсутствуют.
Э лектронно-колебательные
спектры
наблюдаются у любых молекул.
Электронно-колебательный спектр имеет
четко выраженный кант
полос (резкий
край полос) в области длинных волн. Он
обусловлен сгущением энергетических
уровней. Видно, что в пределах полосы
интенсивность линий меняется. Определить
характер распределения интенсивности
линий можно с помощью принципа
Франка-Кондона:
лектронно-колебательные
спектры
наблюдаются у любых молекул.
Электронно-колебательный спектр имеет
четко выраженный кант
полос (резкий
край полос) в области длинных волн. Он
обусловлен сгущением энергетических
уровней. Видно, что в пределах полосы
интенсивность линий меняется. Определить
характер распределения интенсивности
линий можно с помощью принципа
Франка-Кондона:
-
наиболее вероятными являются электронные переходы без изменения расстояния между колеблющимися ядрами атомов и без изменения их скоростей;
-
наиболее вероятными являются электронные переходы, в которых максимумы исходного и конечного состояний расположены на одинаковых межъядерных расстояниях.
Рассмотрим
двухатомную молекулу в основном и
возбужденных состояниях. Возбуждение
молекул приводит к изменению их
электронной конфигурации и к изменению
зависимости энергии от расстояния между
ядрами атомов. Значение энергии
![]() (для основного состояния) также изменяется
и оказывается равным суммарной энергии
изолированных атомов в новом возбужденном
состоянии. За время изменения электронного
состояния молекулы р
(для основного состояния) также изменяется
и оказывается равным суммарной энергии
изолированных атомов в новом возбужденном
состоянии. За время изменения электронного
состояния молекулы р асстояние
между атомами и их скорости не успевают
измениться.
асстояние
между атомами и их скорости не успевают
измениться.
В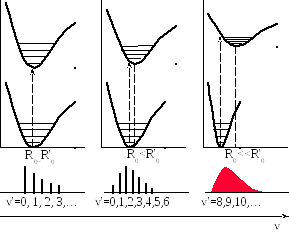 основном состоянии максимум вероятности
колебательных состояний приходится на
основном состоянии максимум вероятности
колебательных состояний приходится на
![]() ,
что соответствует равновесному состоянию
между ядрами. В возбужденном состоянии
максимум плотности вероятности сдвигается
к краям потенциальной ямы. Таким образом,
вероятность электронного перехода
наибольшая лишь при таком расстоянии
между ядрами, при котором вероятности
исходного и конечного состояний
максимальны.
,
что соответствует равновесному состоянию
между ядрами. В возбужденном состоянии
максимум плотности вероятности сдвигается
к краям потенциальной ямы. Таким образом,
вероятность электронного перехода
наибольшая лишь при таком расстоянии
между ядрами, при котором вероятности
исходного и конечного состояний
максимальны.
Если равновесные
расстояния между ядрами атомов в разных
электронных состояниях совпадают (![]() ),
то наиболее вероятным будет переход
без изменения квантового числа
),
то наиболее вероятным будет переход
без изменения квантового числа
![]() .
Этому переходу соответствует наиболее
интенсивная линия в спектре. Если
.
Этому переходу соответствует наиболее
интенсивная линия в спектре. Если
![]() ,
то наиболее вероятен переход из основного
состояния в состояние с небольшим
значением
,
то наиболее вероятен переход из основного
состояния в состояние с небольшим
значением
![]() .
При
.
При
![]() наиболее вероятен переход, соответствующий
диссоциации молекулы (сплошная часть
спектра).
наиболее вероятен переход, соответствующий
диссоциации молекулы (сплошная часть
спектра).
