Принцип тождественности микрочастиц. Принцип Паули.
В классической механике одинаковые частицы (электроны, протоны, элементарные частицы, атомы и т.д.) не теряют своей индивидуальности. Можно проследить за изменением состояния каждой частицы, ее траекторией и импульсом.
В квантовой механике выполняется соотношение неопределенностей, и понятие траектории не имеет смысла.
В квантовой механике одинаковые частицы теряют свою индивидуальность и тождественно неразличимы.
Принцип тождественности (неразличимости) микрочастиц является фундаментальным принципом и состоит в том, что экспериментально различить тождественные частицы невозможно.
Принцип тождественности микрочастиц можно также определить следующим образом: в системе одинаковых частиц реализуются только такие состояния, которые не меняются при перестановке местами двух любых частиц.
Например,
система из 2-х частиц описывается функцией
,
где
и
-
совокупность независимых переменных,
определяемых местоположением и спином
частицы. Если частицы поменять местами,
то функция
может измениться только на фазовый
множитель
(так, чтобы
осталось неизменным). В результате
получаем:
и
,
где
- некоторая вещественная постоянная.
Тогда
.
Из этого
выражения следует, что
,
тогда
.
Это означает, что
=
.
Знаки
”+”
и “-“ означают симметричные и
антисимметричные состояния, определяемые
спином.
Частицы, состояния которых описываются антисимметричными функциями, называются фермионами. Это частицы с полуцелым спином (например, электроны, протоны, нейтроны, нейтрино). Системы, образованные этими частицами, подчиняются статистике Ферми-Дирака.
Симметричные
функции описывают состояния частиц
называемых бозонами.
Это частицы с целым спином, к ним
относятся, например, фотоны,
-
и
-
мезоны. Системы частиц, состоящих из
бозонов, подчиняются статистике
Бозе-Эйнштейна.
Рассмотрим
систему, состоящую из
электронов. Каждая частица может
находиться в одном из состояний
.
Амплитуда вероятности
-
го состояния системы будет
,
где
-
номер частицы.
-
функция – это суперпозиция всех возможных
состояний системы
.
Для системы из 2-х электронов реализуется антисимметричная комбинация:
или
.
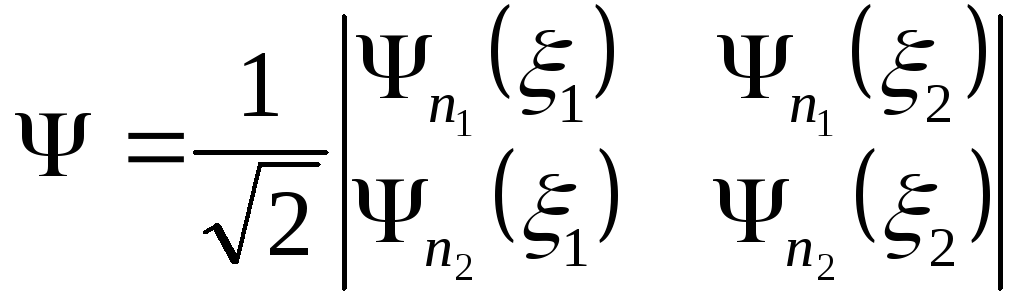Для
системы из
электронов:
.
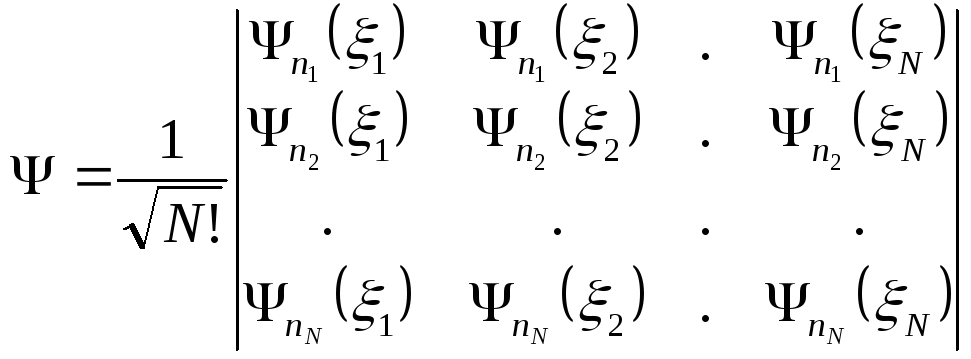Если из
- состояний окажется два одинаковых
состояния, например,
,
то две строки определителя будут
одинаковыми, и определитель станет
равным нулю (из свойств определителя).
Получается, что вероятность такой
ситуации тождественно равна нулю.
Следовательно, для того, чтобы
,
необходимо, чтобы состояния
были различными.
Отсюда следует важный вывод: в системе частиц с полуцелым спином (например, электронов) в одном и том же квантовом состоянии не может находиться более одной частицы. Это – так называемый принцип Паули, установленный в 1925 г.
Следовательно,
в атоме каждый электрон может находиться
в состоянии, характеризуемом квантовыми
числами
,
,
,
.
Распределение электронных состояний в атоме. Периодическая система химических элементов д.И.Менделеева.
Рассмотрим
атом в невозбужденном состоянии.
Состояние каждого электрона этой системы
описывается квантовыми числами
,
,
и
.
Электроны в атомах распределяются по состояниям в определенном порядке в соответствии с принципом Паули, т.е. в каждом состоянии может находиться не более одной частицы с полуцелым спином.
Энергия
электрона определяется главным образом
числами
и
(от взаимной ориентации моментов
и
,
т.е. от квантовых чисел
и
,
энергия электрона зависит значительно
слабее). Совокупность электронов с
одинаковым
образует оболочку (оболочки принято
обозначать буквами
,
,
,
,
и т.д.). Число электронных состояний
(уровней) в оболочке с учетом спина равно
кратности вырождения, т.е. равно
.
Оболочки подразделяются на подоболочки,
отличающиеся значением числа
.
Как же заполняются электронные оболочки атомов?
(
-оболочка);
(
-состояние);
;
2 электрона; форма облака – сфера.
(
-оболочка);
(
-состояние);
;
(
-состояние);
;
8 электронов
;
;
форма облака – 3 гантели, ориентированные в 3-х взаимноперпендикулярных направлениях.
(
-оболочка);
(
-состояние); 
;
(
-состояние); 
;
8 электронов
;
;
(
-состояние); 
;
;
;
18 электронов
;
;
Символы
наглядно обозначают
.
Полностью
заполненные оболочки и подоболочки
имеют
,
и
.
Например,
-подоболочка:
и это единственное значение, поэтому
,
также
(т.к.
),
следовательно,
.
Это
важный результат: при определенных
квантовых числах
и
атома заполненные оболочки можно не
принимать во внимание. Оболочки (или
подоболочки), полностью заполненные
электронами, называют замкнутыми.
Основным термом замкнутых оболочек
(подоболочек) является
.
Закономерность заполнения электронных оболочек в атомах соответствует периодической системе элементов Менделеева.
Если
происходит заполнение только
-оболочки
– это I
период (H,
He),
заполнение
-
и
-оболочкек
– II
период (от Li до Ne), заполнение
-,
-
и
-оболочки
– III период (от Na до Ar,
-
и
-
состояния).
Каждый следующий атом получается из предыдущего добавлением одного электрона, который помещают в разрешенное принципом Паули состояние.
Распределение
электронов в атоме называется электронной
конфигурацией. Например, электронная
конфигурация Na
-
.
Здесь полностью заполнены
-
и
-оболочки.
Электрон в
-
состоянии является валентным. Терм
атома натрия в основном состоянии
.
Следует отметить, что наблюдаемая
периодичность химических и ряда
физических свойств объясняется поведением
именно внешних, валентных электронов.
До
IV
периода заполнение оболочек и подоболочек
имеет «идеальный» характер. В четвертом
периоде дальнейшее заполнение электронных
оболочек происходит не за счет заполнения
- состояния
-
оболочки, а за счет заполнения
-
состояния
-оболочки.
Это происходит из-за того, что уровень
оказывается выше, чем уровень
.
Такая конфигурация является энергетически
более выгодной. Причина - экранировка
ядра атома внутренними электронами.
Влияние экранировки тем больше, чем
больше число электронов в атоме.
Термы основных состояний атомов определяются состояниями валентных электронов.
Термы первых четырех элементов можно легко определить – для этого достаточно принципа Паули:
для
водорода -
,
для
гелия -
,
для
лития -
,
для
берилия -
.
У
бора
пятый электрон занимает одно из
-состояний
(
,
,
или
)
– термы соответствующих состояний
и
.
Какой из этих термов соответствует
основному состоянию атома? Ответить на
этот вопрос
позволяют полуэмпирические правила Хунда:
-
из термов, принадлежащих данной электронной конфигурации наименьшей энергией обладает терм с наибольшим квантовым числом
и наибольшим возможным при данном
числом
; -
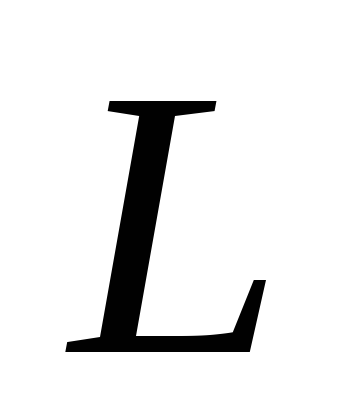при этом полное квантовое число атома принимает значение
,
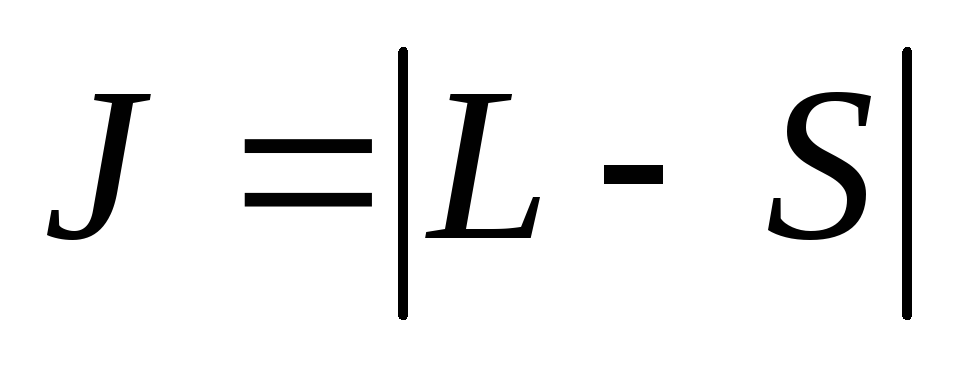если подоболочка заполнена меньше, чем
наполовину, в остальных случаях
.
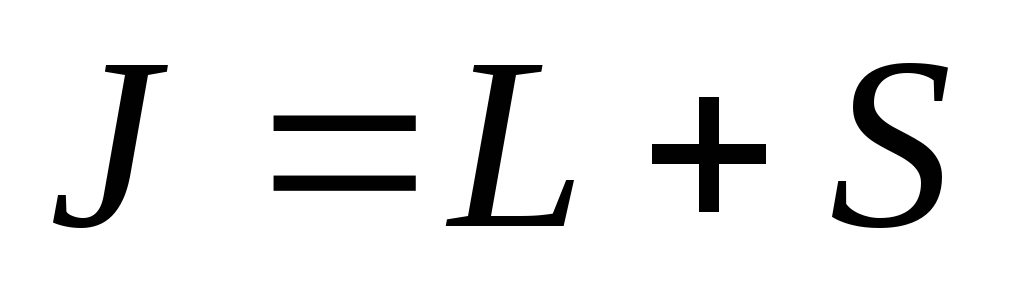Минимальной энергии соответствуют состояния с наибольшим значением суммарного спина, а среди них наименьшим будет уровень с наибольшим орбитальным моментом.