§ 2. Модель реального газа Ван-дер-Ваальса

Для расширения диапазона параметров, в которых поведения газа описывается теоретически, была предложена модель газа Ван-дер-Ваальса, получившую название - модель реального газа. Рассмотрим, как в этой модели учтено взаимодействие между молекулами газа. Межмолекулярное взаимодействие имеет электромагнитную природу. Но атом нейтрален, следовательно, происходит взаимодействие электронейтральных систем. Если расстояние между молекулами велико (много больше линейного размера молекулы), то молекулы, действительно, можно рассматривать как электронейтральные, и, следовательно, практически не взаимодействующие системы. Однако на расстояниях порядка нескольких диаметров молекулы картина меняется.

В среднем в атомах и большинстве простых гомоядерных (состоящих из атомов одного сорта, например, ) молекул распределение положительных и отрицательных зарядов симметрично (неполярные молекулы), однако существуют и такие молекулы (наприме, ), в которых движение электронов приводит к тому, что систему можно рассматривать как электрический диполь (полярные молекулы), и взаимодействие осуществляется между распределенными зарядами.

Если молекулы газа обладают постоянным дипольным моментом , где – расстояние между зарядами в молекуле (полярные молекулы), то между ними появляются силы диполь-дипольного взаимодействия. Диполи стремятся сориентироваться таким образом, чтобы разноименные полюса оказались на минимальном расстоянии.

Как известно, вокруг диполя создаётся электрическое поле, напряжённость которого (при , где - эффективный диаметр молекулы) описывается зависимостью: , где – дипольный момент молекулы. Другая полярная молекула, находясь в этом поле испытывает на себе действие силы

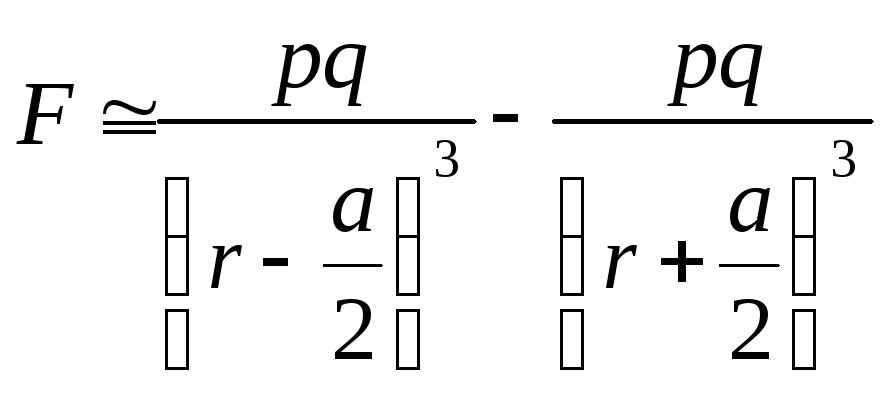(7.2.1)

При где – индуцированный дипольный момент. Индуцированный дипольный момент, в свою очередь, зависит от поля (в первом приближении ). Тогда получаем, что , т.е. силы межмолекулярного притяжения очень быстро убывают с расстоянием. Эти силы носят название сил Ван-дер-Ваальса.

Таким образом, взаимодействие носит характер притяжения и быстро убывает с расстоянием.

Учитывая связь между силой и энергией, получаем, что потенциал сил Ван-дер-Ваальса изменяется обратно пропорционально шестой степени расстояния между молекулами: -потенциал сил Ван-дер-Ваальса.

При сближении структурных единиц на расстояния порядка их размеров, электронные оболочки атомов (или молекул) начинают перекрываться, возникают значительные силы отталкивания, резко растущие с расстоянием.

Экспериментальный вид зависимости потенциальных энергий притяжения, отталкивания и суммарной потенциальной энергии от расстояния между структурными единицами представлены на рис. 7.2.1.

Последовательной теории, или какой-либо универсальной зависимости, описывающей поведение кривой , не существует. В каждом случае выбирается удобная аппроксимация. Часто используется потенциал Ленарда-Джонса: энергия притяжения обратно пропорциональна шестой степени расстояния, а энергия отталкивания – двенадцатой (7.2.2).

, (7.2.2) где .

Минимум потенциальной энергии достигается при расстоянии , а

Если молекулы газа не имеют постоянного дипольного момента (неполярные молекулы), то это не означает, что такой момент не возникает в короткие промежутки времени. В результате теплового движения заряженных частиц, входящих в состав молекул, у последних все время образуются дипольные моменты, разные по величине и направлению. Поэтому лишь в среднем дипольный момент таких молекул равен нулю. Когда такие молекулы сближаются, они поляризуются на короткое время сами и поляризуют близко расположенную молекулу. Таким образом, и в газах с неполярными молекулами появляются силы притяжения за счет диполь-дипольного взаимодействия. Эти силы называются дисперсионными (название связано с тем, что дисперсия света в этих средах обусловлена тем же механизмом поляризации молекул).

Когда молекулы находятся на расстояниях порядка десяти равновесных расстояний, энергия взаимодействия мала и ею можно пренебречь, что соответствует области применимости модели идеального газа.

Энергия отталкивания учитывалась и в модели идеального газа при рассмотрении средней длины свободного пробега путем учета размеров молекул (формула Сезерленда). Если пренебречь температурной зависимостью эффективного радиуса молекул, то молекулы можно представлять непроницаемыми абсолютно твердыми шариками, что и сделано в модели реального газа Ван-дер-Ваальса. При этом реальная зависимость энергии взаимодействия заменяется на модельную. Считается, что энергия взаимодействия при достижении расстояния, равного эффективному радиусу молекулы возрастает до бесконечности (рис.7.2.2).

Какова бы ни была кинетическая энергия молекул, ее не хватит, чтобы преодолеть энергетический барьер: молекула не может изменить своих размеров и размеров других молекул. Таким образом, в модели реального газа учет энергии взаимодействия эквивалентен учету размеров молекул. Проделаем эту процедуру.

В отличие от молекул идеального газа, которые могут находиться в любой точке сосуда, для реальной молекулы недоступен объем, занятый любой другой молекулой. Таким образом, уравнение Менделеева - Клапейрона для одного моля газа будет справедливо для реального газа, если под объемом понимать объем, доступный молекулам. Так как объем отдельной молекулы считается неизменным, то объем, доступный молекулам равен , где b - объем недоступной молекулам части сосуда. Уравнение состояния примет вид

. (7.2.3)

Вычисления показывают, что постоянная b равна учетверенному собственному объему молекулы:

, (7.2.4)

где - эффективный радиус молекулы.

Учтем существование сил притяжения между молекулами. Молекулы оказывают давление на стенку, передавая ей часть импульса при упругом отражении от стенки. Величина импульса, передаваемого стенке молекулами идеального газа, зависит от массы молекулы и ее скорости. Если сила притяжения отлична от нуля, то летящую к стенке молекулу притягивают другие молекулы, модуль ее скорости уменьшается, уменьшается и передаваемый импульс, а следовательно, и эффективное давление, оказываемое на стенку. Сила, действующая на молекулы пристенного слоя, пропорциональна концентрации молекул в этом слое и концентрации молекул следующего слоя, то есть давление реального газа на стенку меньше давления идеального газа на величину, пропорциональную . То есть давление, измеряемое прибором, меньше давления идеального газа на величину , где - некоторая константа. Теперь можно записать уравнение Ван-дер-Ваальса для одного моля реального газа:

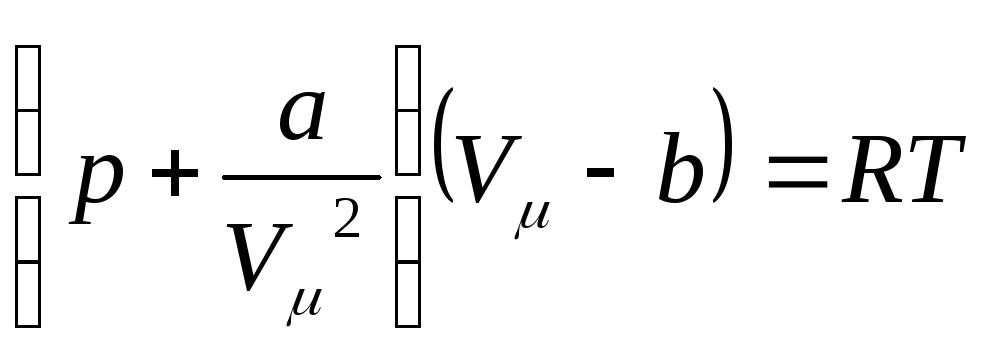. (7.2.5)

Так как в уравнении фигурирует объем одного моля газа, то, осуществив замену , получим уравнение Ван-дер-Ваальса для произвольного количества вещества реального газа

. (7.2.6)

Итак, уравнение Ван-дер-Ваальса описывает поведение реального газа. Молекулы реального газа - абсолютно твердые шарики; сила отталкивания возникает между ними, когда расстояние между центрами молекул равно диаметру молекулы, причем эта сила сразу принимает бесконечное значение.