§ 5. Диффузия

Если молекулы одного сорта газа проникают в среду другого газа (и наоборот), то говорят о взаимной диффузии. Можно наблюдать и так называемое явление самодиффузии, когда меченые (например, радиоактивные) молекулы газа проникают в область, заполненную молекулами того же газа.

Рассмотрим диффузный поток меченых молекул (т. е. самодиффузию). Пусть концентрация этих молекул n (n – зависит от x). Тогда величина G, как характеристика переносимого количества, отнесенная к одной молекуле, приобретает в случае самодиффузии вид , где n₀ – общая концентрация молекул газа. Подставляя величину в общее уравнение процесса переноса, получим

,

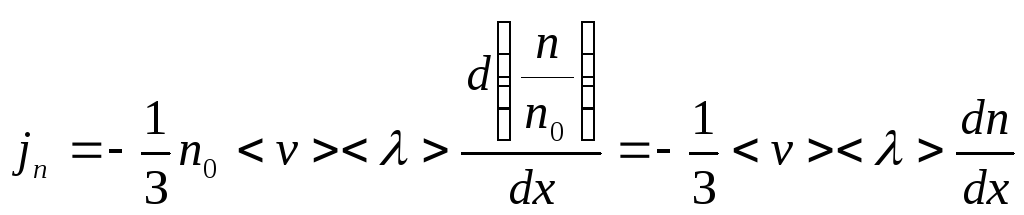умножая это соотношение на массу молекул (m), получим

,

где  – плотность меченых атомов. Сравнение этого соотношения с феноменологическими формулами явления переноса показывает, что коэффициент самодиффузии равен .

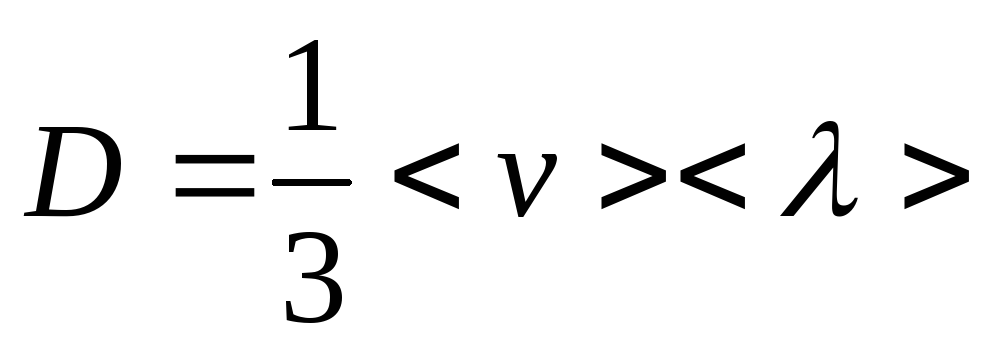Рассмотрим теперь явление взаимной диффузии в смеси двух газов (массы молекул m₁ и m₂ концентрации n₁ и n₂ соответственно). Поскольку давление смеси газов P=n₁kT+n₂kT=(n₁+n₂)kT, то для T=Const и постоянного давления смеси газов P=Const получаем, что n₁+n₂=Const.

Диффузионный поток каждого сорта атомов может быть определен по известной формуле самодиффузии

; ,

где ; .

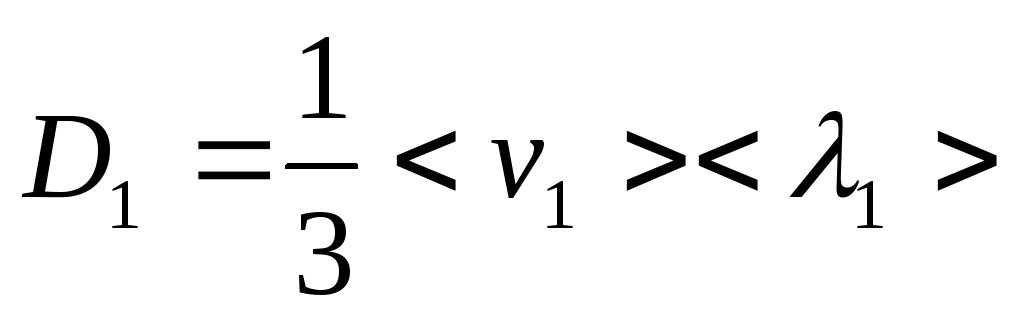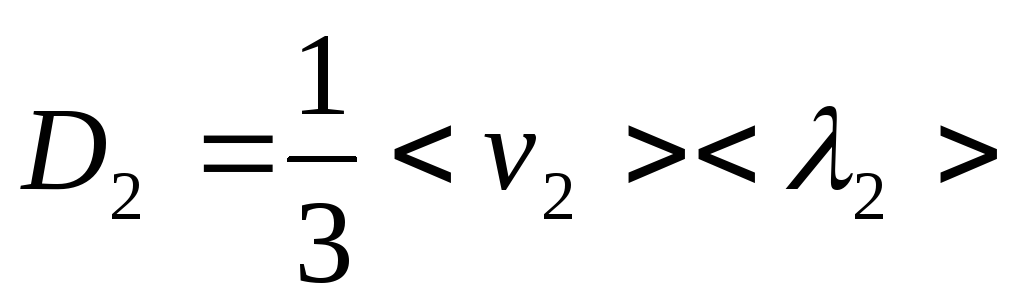В общем случае (т. к. ) и результирующий поток должен привести к изменению концентраций, а значит, и давления в различных областях. Но тогда дополнительно к диффузионному потоку прибавится гидродинамический поток, связанный с возникающей разностью давлений. Пусть скорость гидродинамического потока v. Тогда сам гидродинамический поток через единичную площадку может быть определен следующим образом

.

В равновесии (при P=Const), т. е.

,

т. к. (n₁+n₂=Const),

отсюда

.

Полный (диффузионный и гидродинамический) поток молекул одного сорта может быть определен в виде

.

Таким образом, явление взаимной диффузии описывается выражением подобным выражению самодиффузии

,

где – коэффициент взаимной диффузии (измеряется в м²/с).

Легко показать, что D₁₂=D₂₁. коэффициенты диффузии имеют порядок 10^-5 м²/с для газов при нормальных условиях.

§ 6. Вязкость

Вязкость или внутренне трение в газах, обусловлена переносом импульса молекул перпендикулярно направлению упорядоченного движения слоев газа, если скорости этого движения у разных слоев разные (рис. 2.27). В результате теплового движения молекулы перелетают из одного слоя в другой, перенося свой импульс упорядоченного движения. В результате слой, который двигался быстрее, тормозится, а слой, который двигался медленней, ускоряется. В этом, собственно, и состоит механизм внутреннего трения между слоями, двигающимися с разными скоростями.

В данном случае величина G есть импульс упорядоченного движения молекул p=mv (v – скорость упорядоченного движения). Тогда из общего уравнения переноса получаем

.

Рис.2.27

С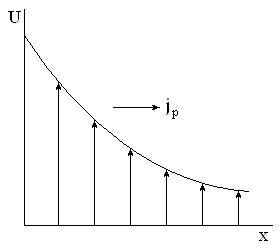равнивая это выражение с феноменологической формулой, получим

Где - динамическая вязкость.

Выражение для впервые было получено в 1860 г. Максвеллом.

Поскольку P (т. к. ), а , то видно, что динамическая вязкость газов не зависит от давления и медленно растет с температурой (т.к. )

Единицей динамической вязкости является паскаль - секунда(Па с). Динамическая вязкость газов при температуре имеет порядок 10 ^–5 Па с. Наряду с динамической вязкостью используется также понятие кинематической вязкости: (ед. измерения 1 м²/с ).

4.6. Теплопроводность.

В этом случае G есть средняя энергия теплового движения, приходящаяся на одну молекулу. Из закона равномерного распределения энергии по степеням свободы имеем:

т.к.

тогда из общего уравнения переноса получаем:

-

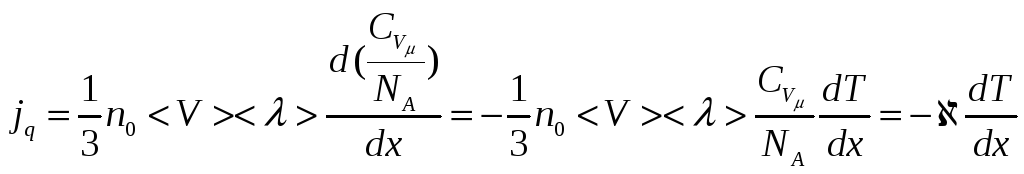(уравнение Фурье), где

Где -удельная теплоемкость при постоянном объеме.

Коэффициент теплопроводности измеряется в Вт/м К.

При постоянной концентрации газа () различие в коэффициенте теплопроводности для разных газов определяется в основном различием их масс молекул газа (т. е. ).

Отсюда видно, что более легкие газы обладают значительно большей теплопроводностью, чем тяжелые. Так, например, кислород имеет Вт/м К, а водород Вт/м К при нормальных условиях. Так же как и вязкость, теплопроводность не зависит от давления газа (в широком диапазоне давлений), так как

, а