
- •Содержание
- •Введение
- •1. Статистические индексы
- •1.1. Основные формулы
- •1.2. Решение типовых задач
- •Решение:
- •Решение:
- •1.3. Контрольные задачи
- •1.4. Контрольные вопросы
- •1.5. Тесты
- •2. Сатистические методы изучения взаимосвязи социально-экономических явлений
- •2.1. Основные формулы
- •2.2. Решение типовых задач
- •Решение:
- •Решение:
- •2.3. Контрольные задачи
- •2.4. Контрольные вопросы
- •2.5. Тесты
- •Библиографический список
2.2. Решение типовых задач
Задача № 2.1
Имеются данные распределения страховых полисов разных агентств по продолжительности заграничной поездки страховщика и стоимостью медицинского страхования:
Таблица 1 – Исходные данные
|
Продолжительность поездки, дни,
|
Количество страховых полисов по стоимости, д.е |
Среднедневная стоимость одного полиса, д.е,
|
||||
|
55-65 |
65-75 |
75-85 |
85-95 |
Итого,
|
||
|
До 8 |
5 |
30 |
85 |
120 |
240 |
83,3 |
|
8-15 |
65 |
50 |
25 |
20 |
160 |
70,0 |
|
15-30 |
75 |
20 |
5 |
- |
100 |
63,0 |
|
Итого |
145 |
100 |
115 |
140 |
500 |
75,0 |
Оценить тесноту связи между рассматриваемыми признаками и проверить ее существенность.
Решение:
Из приведенной
таблицы 1 видно, что каждой группе по
факторному признаку
![]() - продолжительность заграничной поездки
– отвечает определенное условное
распределение страховых полисов по
результативному признаку
- продолжительность заграничной поездки
– отвечает определенное условное
распределение страховых полисов по
результативному признаку
![]() - дневная стоимость страховых полисов.
Условные распределения существенно
отличаются между собой, что свидетельствует
о наличии стохастической связи.
Корреляционную связь можно выявить при
помощи оценок линии регрессии – групповых
средних значений результативного
признака
- дневная стоимость страховых полисов.
Условные распределения существенно
отличаются между собой, что свидетельствует
о наличии стохастической связи.
Корреляционную связь можно выявить при
помощи оценок линии регрессии – групповых
средних значений результативного
признака
![]() ,
рассчитанных по формуле средней
арифметической взвешенной для каждого
интервала по признаку
,
рассчитанных по формуле средней
арифметической взвешенной для каждого
интервала по признаку
![]() .
.
Так, для первой группы полисов по продолжительности поездки до 8 дней имеем:
![]() = (60*5 + 70*30 + 80*85 +
90*120) / 240 = 83,3 д.е;
= (60*5 + 70*30 + 80*85 +
90*120) / 240 = 83,3 д.е;
![]() = (60*65 + 70*50 + 80*25 +
90*20) / 160 = 70,0 д.е;
= (60*65 + 70*50 + 80*25 +
90*20) / 160 = 70,0 д.е;
![]() = (60*75 + 70*20 + 80*5) / 100
= 63,0 д.е,
= (60*75 + 70*20 + 80*5) / 100
= 63,0 д.е,
а для совокупности в целом
![]() = (60*145 + 70*100 + 80*115 +
90*140) / 500 = 75,0 д.е.
= (60*145 + 70*100 + 80*115 +
90*140) / 500 = 75,0 д.е.
Их постепенное изменение (уменьшение) от группы до группы свидетельствует о наличии корреляционной связи. Эффект влияния продолжительности поездки на дневную стоимость страхового полиса определяется как отношение тих приростов:
![]() =
70 – 83,3 = -13,3 д.е;
=
70 – 83,3 = -13,3 д.е;
![]() =
63 – 70 = -7 д.е;
=
63 – 70 = -7 д.е;
![]() =
11,5 – 4,5 = 7 дней;
=
11,5 – 4,5 = 7 дней;
![]() =
22,5 – 11,5 = 11 дней,
=
22,5 – 11,5 = 11 дней,
следовательно, с увеличением продолжительности поездки на 1 день среднедневная стоимость страхового полиса уменьшается в среднем на
![]() /
/![]() = -13,3 / 7 = -1,9 д.е.
= -13,3 / 7 = -1,9 д.е.
Чтобы оценить
тесноту связи при помощи корреляционного
отношения
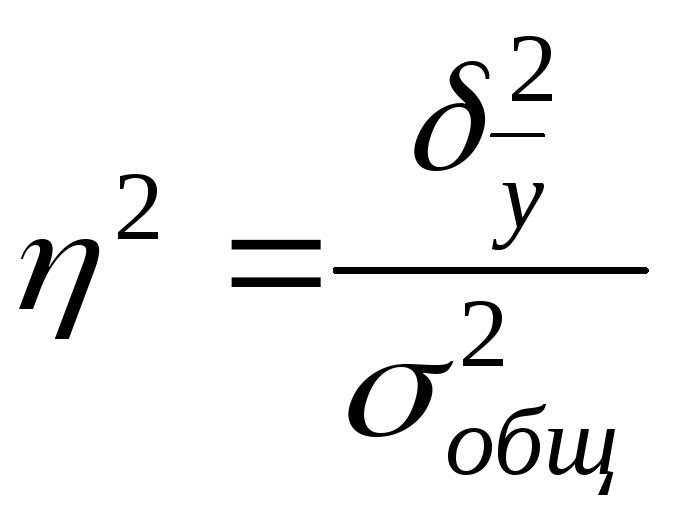 , необходимо
рассчитать соответствующие дисперсии.
Общая дисперсия стоимости страховых
полисов рассчитывается по следующей
формуле:
, необходимо
рассчитать соответствующие дисперсии.
Общая дисперсия стоимости страховых
полисов рассчитывается по следующей
формуле:
![]() ,
где
,
где
![]() ;
;
![]() =5764–5625=139.
=5764–5625=139.
Расчет межгрупповой дисперсии представлен в таблице 2:
Таблица 2 – Аналитическая группировка страховых полисов по их дневной стоимости в зависимости от продолжительности поездки
|
Продолжительность поездки, дни,
|
Количество страховых полисов,
|
Среднедневная стоимость одного полиса, д.е,
|
|
|
|
До 8 |
240 |
83,3 |
8,3 |
16533,6 |
|
8-15 |
160 |
70,0 |
-5,0 |
4000,0 |
|
15-30 |
100 |
63,0 |
-12,0 |
14400,0 |
|
Итого |
500 |
75,0 |
|
34933,6 |
Межгрупповая дисперсия определяется по формуле:
![]() .
.
Тогда
![]() .
Таким образом, вариация стоимости
страховых полисов на 50,3 % обусловлена
вариациею продолжительности поездки
и на 49,7 % - вариациею других факторов.
Поэтому связь между признаками достаточно
сильная.
.
Таким образом, вариация стоимости
страховых полисов на 50,3 % обусловлена
вариациею продолжительности поездки
и на 49,7 % - вариациею других факторов.
Поэтому связь между признаками достаточно
сильная.
Чтобы проверить
существенность связи, берут критическое
значение
![]() .
Из таблицы 2 определяем
.
Из таблицы 2 определяем
![]() =
3-1 =2,
=
3-1 =2,
![]() =
500 -3 = 497, следовательно,
=
500 -3 = 497, следовательно,
![]() =
0,015. Так как
=
0,015. Так как
![]() =0,503>0,015,
то связь считается существенной с
вероятностью 0,95.
=0,503>0,015,
то связь считается существенной с
вероятностью 0,95.
Задача № 2.2
Исследовать данные маркетингового обследования эффективности использования рекламного времени, представленные в следующей таблице:
|
Место рекламы в эфирном времени |
Количество респондентов, которые смотрят телерекламу |
Итого |
|
|
внимательно |
невнимательно |
||
|
Во время фильма |
45 |
15 |
60 |
|
Перед фильмом |
12 |
28 |
40 |
|
Итого |
57 |
43 |
100 |
