Метод Гаусса

Метод Гаусса основан на привидении матрицы системы к треугольному виду, а в обратной последовательности к решению.

Сначала на первом шаге с помощью первого уравнения исключается х первое из всех последовательных уравнений системы, в результате получается новая система, имеющая то же решение, но в первом столбце матрицы будет не нулевой только первый, а все остальные обращаются в нуль. На втором шаге исключается х₂ из всех уравнений. Этот процесс продолжается до тех пор, пока в левой части последовательного n-го уравнения остается лишь один член с неизвестным х_n.

Рассмотрим процесс исключения подробнее. На к-ом шаге используется х_k. Запишем k-ое уравнение

Исключим с помощью этого уравнения x_k из уравнения с номером i>k

Из i-го уравнения вычитаем k-ое умножимое на a_ik/a_kk после такого вычисления первое слагаемое сокращается. Запишем значение аргумента перед х.

при этом изменится свободный член:

По завершению прямого хода получается система с треугольной матрицей. Далее производится обратный ход метода Гаусса. Он состоит в последовательном вычислении малых неизвестных начиная с х_n. Сначала находится

Далее используя это значение, находится х_n-1 и док далее. На k-ом шаге обратного хода неизвестные находятся с помощью выражения: . В процессе исключения неизвестных приходится делить. Чтобы исключить эту ситуацию необходимо на каждом шаге прямого хода метода Гаусса менять расположение, чтобы a_kk≠0, а лучше, чтобы он имел максимально возможное значение. Переустановка уравнений должна быть предусмотрена в одном из уравнений и метод Гаусса, в котором производится перестановка уравнений таким образом, чтобы диагональный элемент имел значение, называемый элементом Гаусса с главным значением. В методе Гаусса объем вычислений пропорционален n³. Существуют практически значимые случаи, когда объем вычислений систем линейных уравнений можно резко сократить.

Метод №15

Метод прогонки

Метод прогонки является модификацией метода Гаусса для частного случая систем уравнений с трех диагональной матрицей. Такие системы возникают при численном решении уравнений математической физики. Коэффициент сплайна третьей степени находится путем решения систем с трех диагональной матрицей. В методе прогонки объем вычислений растет пропорционально n. Запишем систему уравнений, которая решается методом прогонки:

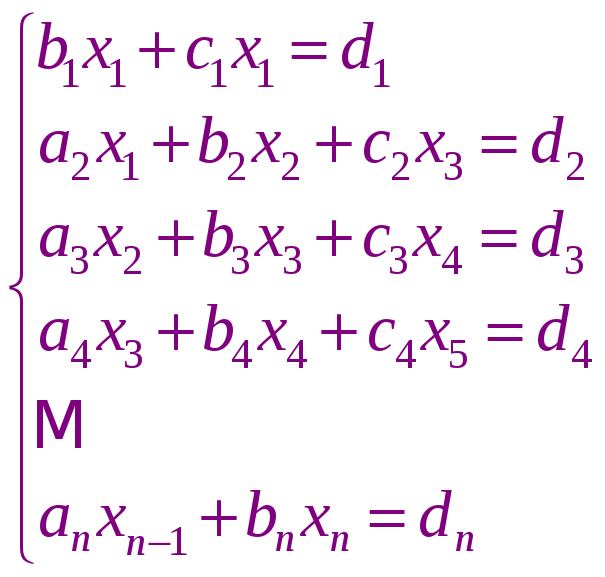
Общий вид уравнения:

Решение системы с трех диагональной матрицей, как и в методе Гаусса, состоит из двух этапов: прямой прогонки и обратной прогонки.

Рассмотрим первый этап (прямой ход):

Для этого неизвестное x_i выражаем через x_i+1 таким образом x_i , где A_i и B_i неизвестные пока коэффициенты (прогоночные). На первом этапе как раз и находятся A_i и B_i. Сравним x_i = A_ix_i+1 + B_i , i=1, x₁ = A₁x₂ + B₁

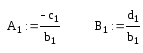
Запишем i-ое уравнение системы, выразим в нем x_i-1 с помощью

Сравнивая эти соотношения, получаем реккурентные соотношения для нахождения прогоночных коэффициентов.

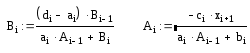
После того как найдены все прогоночные коэффициенты, в результате прямого хода метода находим х_n, для этого сравниваем последнее уравнение системы a_nx_n-1 + b_nx_n = d_n с последним прогоночным соотношением x_n-1 = A_n-1x_n + B_n-1 получается система: .

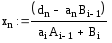Метод №16