Тема №4 Решение систем линейных уравнений.
Системы линейных алгебраических уравнений (СЛАУ) в научно-исследовательской инженерной практике встречаются весьма часто. К решению систем линейных уравнений сводится многочисленные практические задачи с использованием численных методов.
Например:
Коэффициенты сплайнов находятся путем решения СЛАУ. К СЛАУ приводят уравнения частных производных.
Задачи по нахождению собственных значений также приводят к СЛАУ. Таким образом, решение СЛАУ – одна из самых распространенных и важных задач вычислительной математики.
Запишем СЛАУ в общем виде:
-
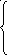
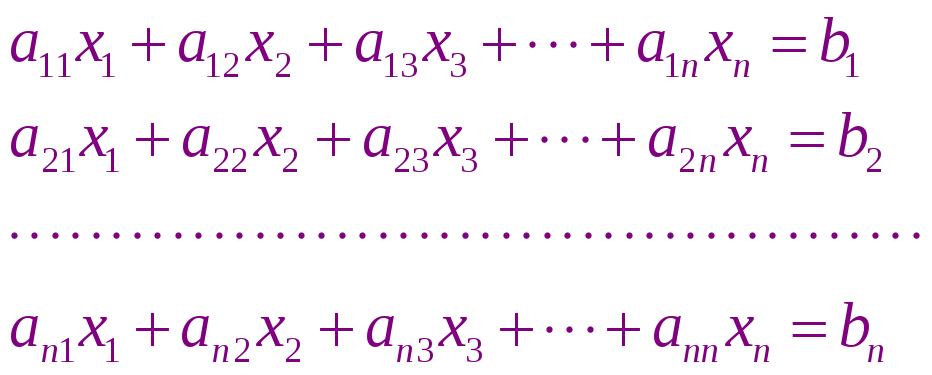
номер уравнения
- номер неизвестной, на которую умножается
коэффициент.
Коэффициенты образуют матрицу
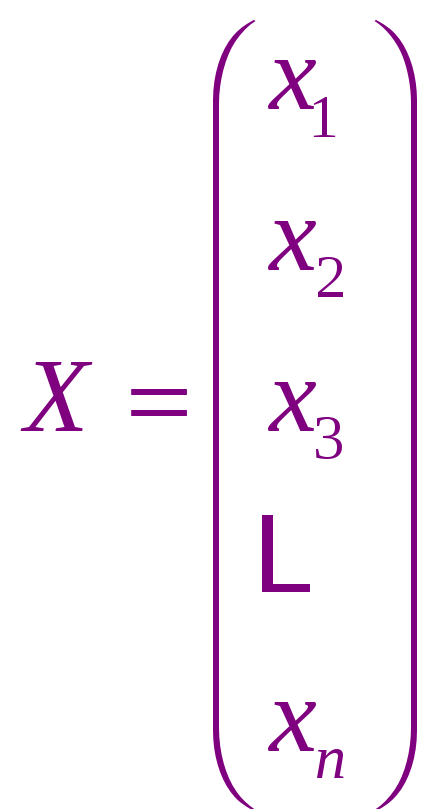
Матрица системы столбец неизвестных величин столбец правых частей
Введя эти величины, мы можем записать СЛАУ в виде матричного решения
Важнейшей характеристикой квадратной
матрицы является её определитель(
)
Число возможных значений
В курсе высшей математики показывается, что система СЛАУ имеет единственное решение, если определитель системы не равен нулю. В этом случае решение может быть найдено с помощью формул Крамера:
,
где
- определитель матрицы, которая получается
после исключения в матрице А
-го
столбца и его замены столбцом свободных
членов.
Если определитель системы равен нулю,
то в этом случае матрица
называется вырожденной,
а система либо не имеет
решения, либо
имеет бесконечное множество решений.
Для некоторых систем решение оказывается
очень чувствительным к малым погрешностям
в исходных данных
.
Такие системы называются плохо-обусловленными.
Определитель плохо-обусловленных систем
близок к нулю. При численных вычислениях
всегда надо иметь ввиду эту особенность
систем линейных уравнений.
Существуют методы улучшения обусловленности систем. Некоторые некорректные задачи приводят к плохо обусловленным системам уравнений. Эти задачи могут иметь важное практическое значение. Существуют методы решения таких задач.
Методы решения СЛАУ делятся на 2 группы:
1) Прямые
используют готовые формулы для вычисления
неизвестных, эти методы наиболее
универсальны, пригодны для решения
широкого класса СЛАУ. Но они обладают
недостатками: они требуют
хранения в оперативной памяти сразу
всей матрицы. Существенным
недостатком прямых методов является
накапливание погрешности
в процессе решения. Это особенно
опасно для больших систем, а также для
плохо-обусловленных , поэтому прямые
методы используют обычно если
нескольких
сотен.
2) Итерационные
в итерационных методах решение находят путем последовательных приближений. Накапливание погрешности не происходит, и с помощью них решают систему с большим числом уравнений и для решения плохо-обусловленных систем. Однако сходимость итерации может быть очень медленной. Поэтому время счета может быть очень большим. Другим недостатком является то, что с их помощью решается ограниченный класс уравнений.
Например:
Уравнений с преобладанием диагональных элементов, либо системы со слабо заполненными матрицами.
Метод Крамера относится к прямому
методу, однако на практике метод Крамера
практически никогда не используется,
так как он требует большого объёма
вычислений. Оценим объём вычислений с
помощью метода Крамера. Для применения
этого необходимо вычислить
определитель, а для вычисления каждого
определителя необходимо сделать
произведений, а число полученных
слагаемых
.
Значит, число арифметических операций
будет
с ростом
резко возрастает при
Наиболее распространенным среди прямых методов является метод Гаусса.
Метод 14