Метод Эйлера.

Простейшим методом решения обыкновенного дифференциального уравнения первого порядка является метод Эйлера.

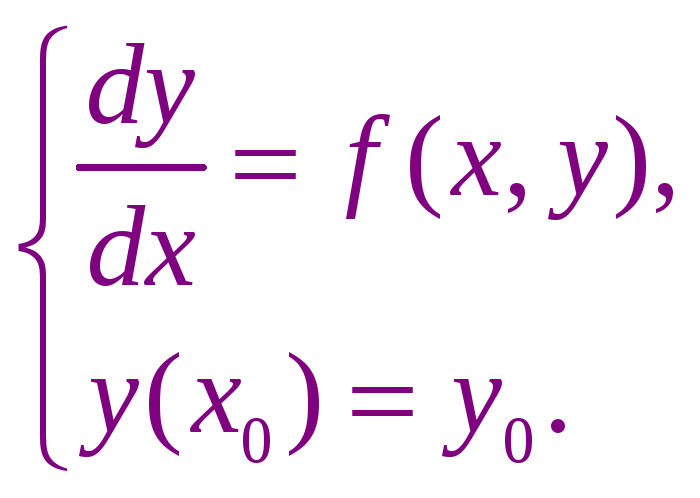
Требуется найти . Как зависит от .

Будем находить решение в точках отстоящих друг от друга на расстоянии h (шаг задачи). Допустим решение в точке известно, и требуется найти значение неизвестной в точке . Разложим решение в окрестности точки в ряд Тейлора:

В этом ряде ограничимся первыми двумя слагаемыми

В результате получаем простейшую формулу

, которая реализует метод Эйлера .

, ,

точность

погрешность на одном шаге.

Таким образом, погрешность метода Эйлера равна .

Метод 29

Модифицированный метод Эйлера.

Точность метода Эйлера можно существенно повысить, улучшив аппроксимацию производной. В модифицированном методе Эйлера сначала вычисляется значение,

которое используется для вычисления приближенного значения производной в конце интервала . Значение производной полагают равным .

Мы нашли, что в начале интервала значение производной равно

, а в конце

Для нахождения на интервале удобно использовать среднее значение.

Такое представление производной тождественно использованию в ряде Тейлора членов пропорциональных .

Метод 30

Метод Рунге – Кутта.

Это метод, который позволяет учесть в ряде Тейлора члены, содержащие старшие производные.

Для этого при вычислении старших производных используется результаты расчетов в точках внутри интервала. Метод Рунге – Кутта объединяет целое семейство методов решения дифференциальных уравнений первого порядка. Отличаются эти методы порядком точности, т.е. числом слагаемых в ряде Тейлора.

Наиболее распространенным является метод, при котором удерживаются члены пропорциональные (метод 4-го порядка точности) когда говорят метод Рунге-Кутта, то имеют в виду метод четвёртого порядка.

Расчеты в этом методе производятся по следующим формулам

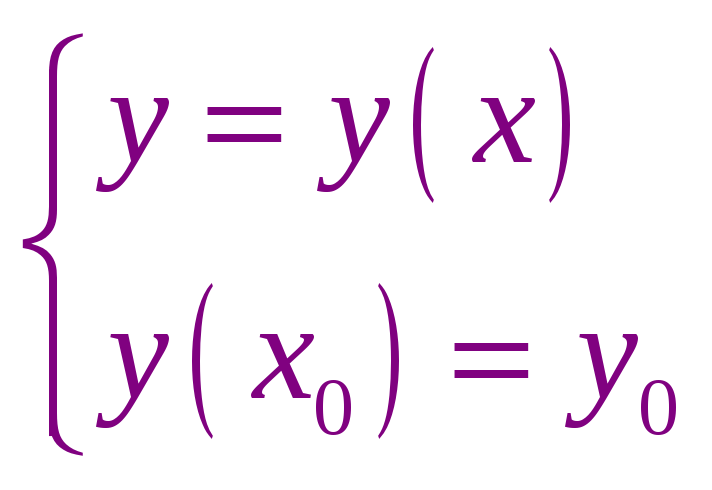
Метод 31

Метод Рунге-Кутта для решения систем оду

Метод Рунге – Кутта может применяться для решения систем дифференциальных уравнений первого порядка. Например: при решении системы

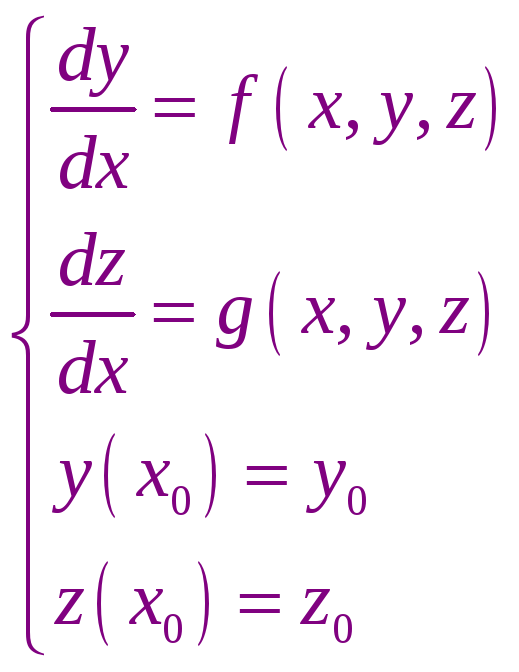найдем

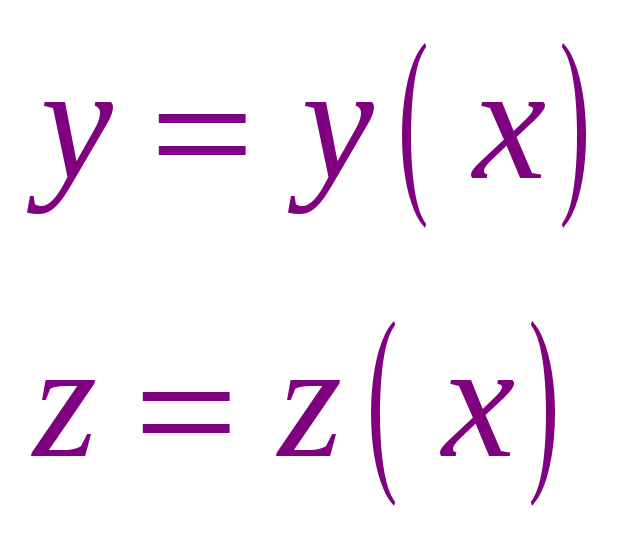
В этом случае расчеты производятся по следующим формулам:

Метод 32

Метод Рунге-Кутта для оду высших порядков.

Метод Рунге – Кутта можно использовать для решения дифференциальных уравнений высокого порядка (второго или более высокого). Для этого дифференциальное уравнение сводится к системе уравнений первого порядка.

Например: дифференциальное уравнение второго порядка:

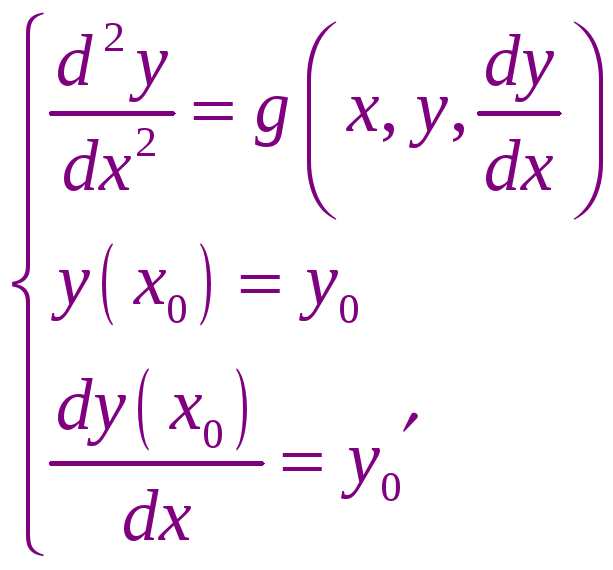
Введём переменную , в результате решаемая задача приводится к следующей задаче:

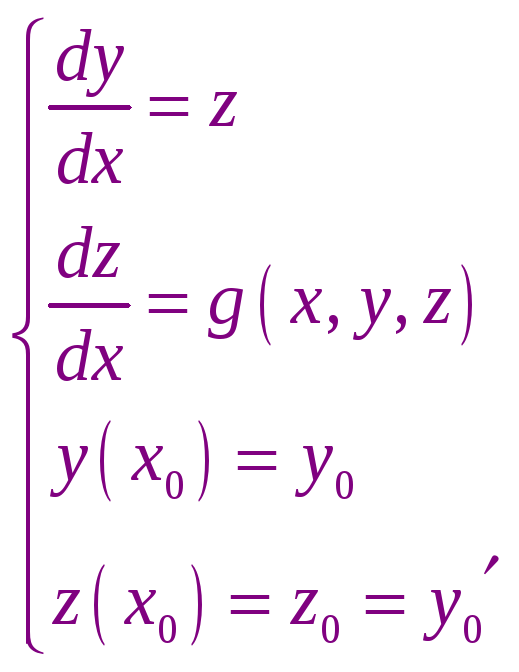получили систему двух уравнений первого порядка.

Метод 33

Метод стрельбы.

Методы решения задачи Коши могут быть использованы при решении краевых задач. В качестве примера рассмотрим один из методов решения краевой задачи для дифференциального уравнения второго порядка, который называется методом стрельбы.

Решается дифференциальное уравнение второго порядка:

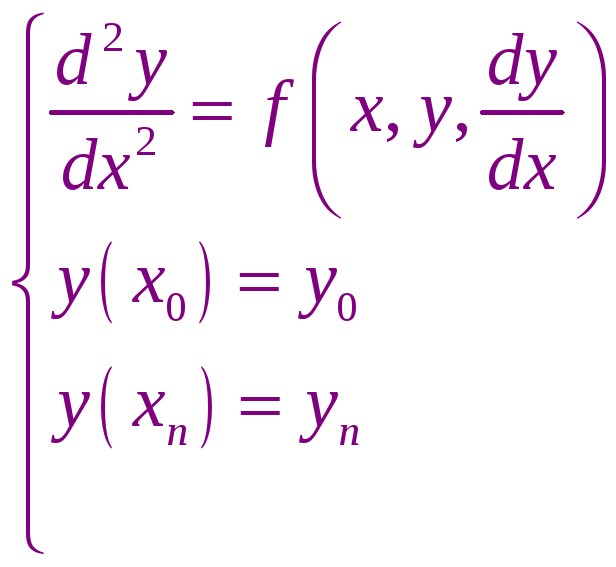
Заменим эту краевую задачу задачей Коши

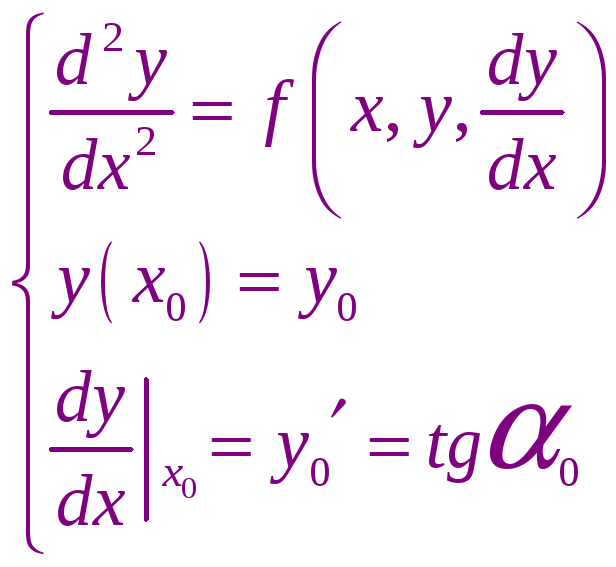
Задача сводится к тому, чтобы найти такой угол , чтобы в точке решение равнялось .

Эта задача зависит от угла , как от параметра:

И нужно чтобы

Решение этого уравнения есть . Найдя, мы тем самым решим задачу как методом Коши.

Метод 34