2.4. Способы преобразования проекций. Построение развертки.
Развертка – это _____________________________________________________
____________________________________________________________________________________________________________________________________.
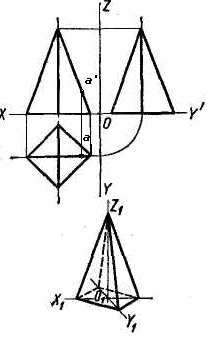
Н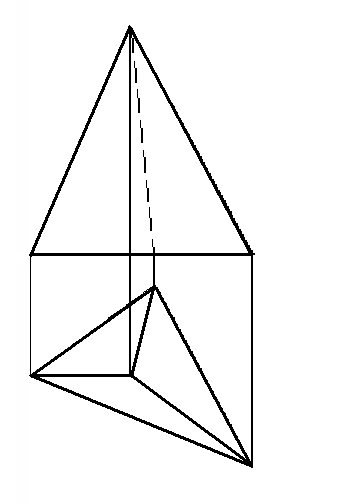
айти
натуральные
величины ребер пирамиды и построить ее
развертку
Тема 2.5. Сечение геометрических тел плоскостями
2.5.1.Сечение пирамиды
Построить горизонтальную, профильную проекции, натуральную величину сечения, изометрию и развертку усеченной пирамиды
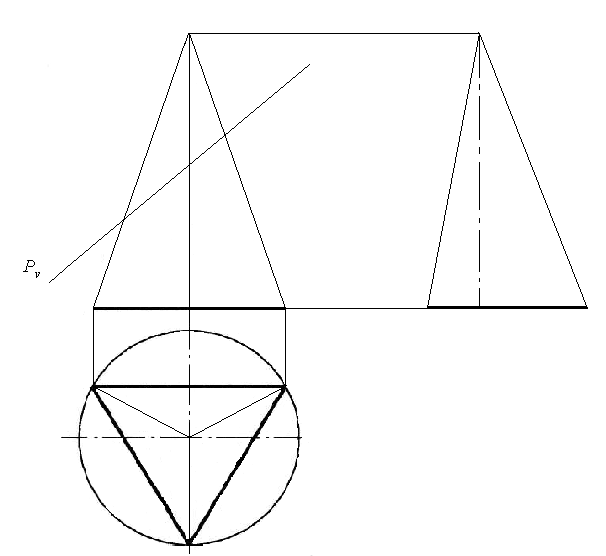
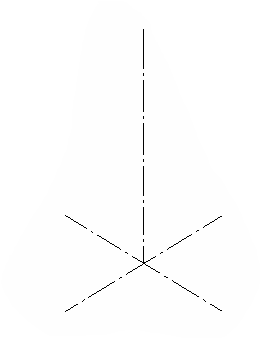
Развертка поверхности пирамиды
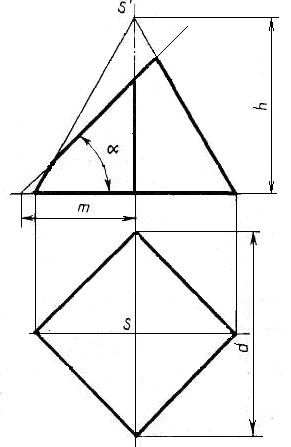
Задание 2.3. Построить комплексный чертеж, изометрию и развертку усеченной четырехугольной пирамиды.
|
№ варианта |
Обозначение |
|||
|
h |
d |
m |
α |
|
|
1 |
65 |
60 |
40 |
45 |
|
2 |
70 |
55 |
35 |
35 |
|
3 |
80 |
70 |
40 |
45 |
|
4 |
65 |
70 |
50 |
30 |
|
5 |
75 |
60 |
20 |
50 |
|
6 |
70 |
55 |
20 |
50 |
|
7 |
80 |
60 |
20 |
50 |
|
8 |
90 |
70 |
25 |
35 |
|
9 |
65 |
70 |
30 |
45 |
|
10 |
75 |
60 |
25 |
50 |
|
11 |
70 |
50 |
35 |
45 |
|
12 |
80 |
60 |
40 |
35 |
|
13 |
75 |
60 |
30 |
45 |
|
14 |
90 |
70 |
25 |
30 |
|
15 |
70 |
60 |
20 |
45 |
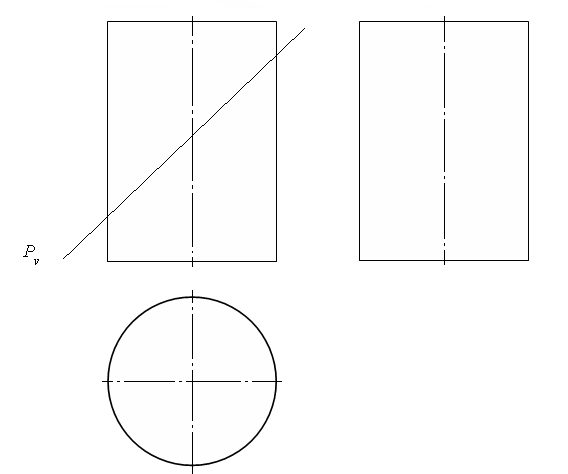
2.5.2. Сечение цилиндра
Построить горизонтальную, профильную проекции, натуральную величину сечения, изометрию и развертку усеченного цилиндра.
Тесты к темам 2.3-2.5.
|
1.Выберите элементы поверхности геометрических тел |
1) цилиндра:
|
Нижнее основание |
|
Верхнее основание |
||
|
Грани |
||
|
2) пирамиды: |
Боковая поверхность |
|
|
Ребра |
||
|
Вершины |
||
|
2.
|
В какой аксонометрической проекции изображен конус?
|
Косоугольная диметрия |
|
Прямоугольная изометрия |
||
|
Прямоугольная диметрия |
||
|
На какой проекции конуса все образующие проецируются в искаженном виде? |
На фронтальную |
|
|
На горизонтальную |
||
|
На профильную |
||
|
Будет ли видимой фронтальная проекция образующей SA? |
Да |
|
|
Нет |
||
|
3.
|
На какой проекции видны все боковые грани пирамиды
|
На фронтальной |
|
На горизонтальной |
||
|
На изометрической |
||
|
На профильной |
||
|
Сколько ребер пирамиды проецируются на фронтальную плоскость проекций в натуральную величину? |
три |
|
|
два |
||
|
четыре |
||
|
Где лежит точка А |
На ребре основания |
|
|
На боковом ребре |
||
|
На грани |
||
|
4.Какая фигура получится при сечении конуса плоскостью параллельной основанию? |
Эллипс |
|
|
Овал |
||
|
Круг |
||
|
Треугольник |
||
|
5.Какая фигура получится при сечении цилиндра плоскостью перпендикулярной основанию? |
Круг |
|
|
Эллипс |
||
|
Прямоугольник |
||
|
Овал |
||
