
- •Принципы построения, устойчивость и точность численных методов
- •Явные численные методы решения обыкновенных дифференциальных уравнений
- •Явный метод Эйлера
- •Метод Рунге – Кутта – Мерсона
- •Метод Адамса – Башфорта
- •Методы Фельберга
- •Методы Ингленда
- •Методы Нюстрема
- •Явные методы Милна
- •Явные методы Хемминга
- •Экстраполяционные методы
- •Неявные методы Милна
- •Неявные методы Хемминга
- •Методы дифференцирования назад
- •Неявные методы Рунге-Кутта
- •Описание математической модели солнечной системы и параметры ее траектории.
- •Определение и свойства моделей
- •Развитие модели Солнечной системы
- •Описание модели Солнечной системы
- •Преобразование координат в плоскости орбиты
- •Определение положения планеты на орбите в новый момент времени
- •Алгоритм прогнозирование величины радиуса
- •Алгоритм прогнозирования угла
- •Дополнительные условия
- •Вычисление декартовых координат
- •Начальные данные.
- •Вычисления и сравнения.
- •Литература
-
Явные методы Милна
Многошаговый метод Милна четвертого порядка точности может быть реализован двумя различными способами:

или


Для начала расчетов по формулам указанным выше требуется четыре «разгонные» точки X0, X1, X2, X3. В методе Милна шестого порядка точности для расчета используется шесть предыдущих точек, которые могут быть найдены любым из предыдущих методов.
-
Явные методы Хемминга
Многошаговый
метод Хемминга четвертого порядка
точности может быть реализован тремя
различными способами, в каждом из которых
для нахождения точки
 используются четыре предыдущие точки:
используются четыре предыдущие точки:
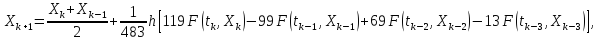

или



или



Для начала расчетов по любой из формул указанных выше требуется четыре «разгонные» точки X0, X1, X2, X3.
-
Экстраполяционные методы
Экстраполяционные методы основаны на том факте, что глобальная погрешность численного решения порядка p допускает разложение в степенной ряд по h:
|
|
(28) |
где
 - приближенное решение на отрезке k,
полученное на равномерной сетке с шагом
h.
- приближенное решение на отрезке k,
полученное на равномерной сетке с шагом
h.
Формула
(28) представляет приближенное решение
на фиксированном отрезке k,
как функцию
 . Для этой функции
. Для этой функции
 .
.
Теоретически
это означает, что при достаточно малом
шаге можно любым методом получить
приближенное решение со сколь угодно
высокой точностью. С практической точки
зрения использование очень малых шагов
не разумно, поскольку, во-первых, это
увеличивает объем вычислений, что,
во-вторых, сопряжено с большими ошибками
округления. Тем не менее, используя идею
экстраполяции, можно получить с высокой
точностью предельное значение
 ,
избегая при этом многочисленных
вычислений.
,
избегая при этом многочисленных
вычислений.
-
Неявные численные методы решения обыкновенных дифференциальных уравнений
-
Неявный метод Эйлера
В
неявном методе Эйлера для вычисления
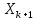 используется формула:
используется формула:

В
данном случае искомая величина
 ,
в
отличии от явного метода Эйлера, входит
в обе части равенства. Неявный метод
Эйлера является А-устойчивым для линейных
систем ОДУ и имеет первый порядок
точности относительно шага h.
,
в
отличии от явного метода Эйлера, входит
в обе части равенства. Неявный метод
Эйлера является А-устойчивым для линейных
систем ОДУ и имеет первый порядок
точности относительно шага h.
-
Метод трапеций
В
методе трапеций для вычисления
 используется формула:
используется формула:

как
и в неявном методе Эйлера случае искомая
величина
 ,
входит
в обе части равенства. Метод трапеций
является А-устойчивым для линейных
систем ОДУ и имеет второй порядок
точности относительно шага h.
,
входит
в обе части равенства. Метод трапеций
является А-устойчивым для линейных
систем ОДУ и имеет второй порядок
точности относительно шага h.
-
Метод Адамса – Мултона
В
методе Адамса - Мултона для вычисления
 используется формула:
используется формула:

и,
как и ранее, искомая величина
 ,
входит
в обе части равенства. Метод является
двух шаговым. Для начала расчета
требуется две «разгонные» точки X0,
X1.
Метод
не является устойчивым и имеет четвертый
порядок
точности относительно шага h.
,
входит
в обе части равенства. Метод является
двух шаговым. Для начала расчета
требуется две «разгонные» точки X0,
X1.
Метод
не является устойчивым и имеет четвертый
порядок
точности относительно шага h.
Неявный метод Эйлера и метод трапеций относятся к группе методов Адамса – Мултона, а выделены отдельно в силу их большой распространенности.
-
Неявные методы Милна
В
неявных методах Милна (третьего и
четвертого порядка точности) для
вычисления точки
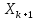 используются формулы:
используются формулы:

в методе третьего порядка точности и


в методе четвертого порядка точности.
Для начала расчетов требуется иметь две и три «разгонные» точки соответственно. Формулы, в которых используется большее число предыдущих точек, приведены в [4].

