- •Принципы построения, устойчивость и точность численных методов
- •Явные численные методы решения обыкновенных дифференциальных уравнений
- •Явный метод Эйлера
- •Метод Рунге – Кутта – Мерсона
- •Метод Адамса – Башфорта
- •Методы Фельберга
- •Методы Ингленда
- •Методы Нюстрема
- •Явные методы Милна
- •Явные методы Хемминга
- •Экстраполяционные методы
- •Неявные методы Милна
- •Неявные методы Хемминга
- •Методы дифференцирования назад
- •Неявные методы Рунге-Кутта
- •Описание математической модели солнечной системы и параметры ее траектории.
- •Определение и свойства моделей
- •Развитие модели Солнечной системы
- •Описание модели Солнечной системы
- •Преобразование координат в плоскости орбиты
- •Определение положения планеты на орбите в новый момент времени
- •Алгоритм прогнозирование величины радиуса
- •Алгоритм прогнозирования угла
- •Дополнительные условия
- •Вычисление декартовых координат
- •Начальные данные.
- •Вычисления и сравнения.
- •Литература
-
Метод Рунге – Кутта – Мерсона
Отличие этого метода от классического метода Рунге-Кутты четвертого порядка состоит в том, что шаг интегрирования вычисляется автоматически в зависимости от текущей точности.
Алгоритм приближенного решения системы дифференциальных уравнений методом Рунге – Кутта – Мерсона заключается в следующем:
-
Задается погрешность и начальный шаг интегрирования h.
-
Для расчета точки
 используется формула
используется формула
|
|
(24) |
где
|
|
|
Вычисляется погрешность:
 .
.
Проверяются
условия:
 .
.
Если оба условия выполняются, то расчет продолжается с тем же шагом. Если не выполняется первое условие, то текущий шаг делится пополам и процесс повторяется с п.2. Если не выполняется второе условие, то текущий шаг увеличивается вдвое и процесс повторяется с п.2.
Метод имеет четвертый порядок точности относительно шага h.
-
Метод Адамса – Башфорта
В
многошаговом методе Адамса – Башфорта
третьего порядка точности для нахождения
точки
 используется
три предыдущие точки:
используется
три предыдущие точки:
|
|
(25) |
Для начала расчетов требуются три «разгонные» точки X0, X1, X2, которые можно получить любым из предыдущих методов.
В
многошаговом методе Адамса – Башфорта
четвертого порядка точности для
нахождения точки
 используется
четыре предыдущие точки, а для начала
расчетов требуется четыре «разгонные»
точки.
используется
четыре предыдущие точки, а для начала
расчетов требуется четыре «разгонные»
точки.
|
|
Методы Адамса - Башфорта не позволяют изменять шаг в процессе расчетов. В отличии от метода Рунге-Кутты четвертого порядка в этих методах требуется вычислить только одно новое значение правой части системы (12) вместо четырех. Высокая точность методов достигается при этом за счет учета информации о предыдущих точках. В методе Рунге – Кутты, как и в других одношаговых методах, недостающую информацию о поведении правых частей системы получают в результате вычислений в специальным образом выбранных дополнительных точках.
-
Методы Фельберга
В
методе Фельберга пятого порядка точности
для расчета точки
 используется
формула
используется
формула

где
|
|
(26) |
В
методе Фельберга четвертого порядка
точности для расчета точки
 используется
формула
используется
формула

где коэффициенты k1, k2, k3, k4, k5 определяются согласно (26).
-
Методы Ингленда
В
методе Ингленда пятого порядка точности
для расчета точки
 используется
формула
используется
формула

где
|
|
(27) |
В
методе Ингленда четвертого порядка
точности для расчета точки
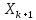 используется
формула
используется
формула
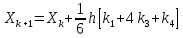
где коэффициенты k1, k3, k4 определяются согласно (27).
-
Методы Нюстрема
В
многошаговых методах Нюстрема второго,
третьего и четвертого порядка точности
для нахождения точки
 используются
две, три и четыре предыдущие точки
соответственно:
используются
две, три и четыре предыдущие точки
соответственно:




Для начала расчетов по выше указанным формулам требуются две, три и четыре «разгонные» точки соответственно. В практических задачах часто возникает необходимость решения дифференциального уравнения второго порядка. Для решения таких уравнений существует метод Нюстрема пятого порядка точности. Другие специальные методы решения уравнений второго порядка изложены в [3].

















 ,
,